3 Симплексная таблица

Базис	B	x1	x2	x3	x4	x5
x3	1/5	1/5	-4/5	1	–14/5	0
x5	1/6	1/5	1/5	0	1/5	1
	11/5–F	-9/5	1/5	0	16/5	0

Полученное базисное решение также не является оптимальным, т.к. и . Согласно правилу №3 необходимо искать оптимальное решение путем пересчета симплексной таблицы.

После пересчета составлятся четвертая симплексная таблица:

4 Симплексная таблица

Базис	B	x1	x2	x3	x4	x5
x3	17	3	2	1	0	14
x4	6	1	1	0	1	1
	-17–F	-5	-3	0	0	-16

В четвертой симплексной таблице среди элементов последней строки нет ни одного положительного. Поэтому четвертое базисное решение является оптимальным.

Ответ.

Оптимальное базисное решение:

Наименьшее значение линейной формы:

.

Пример №2.5.

Предприятие может выпускать четыре вида продукции ( ), используя для этого три вида ресурсов ( ). Известна технологическая матрица затрат любого ресурса на единицу каждой продукции, вектор объемов ресурсов и вектор удельной прибыли:

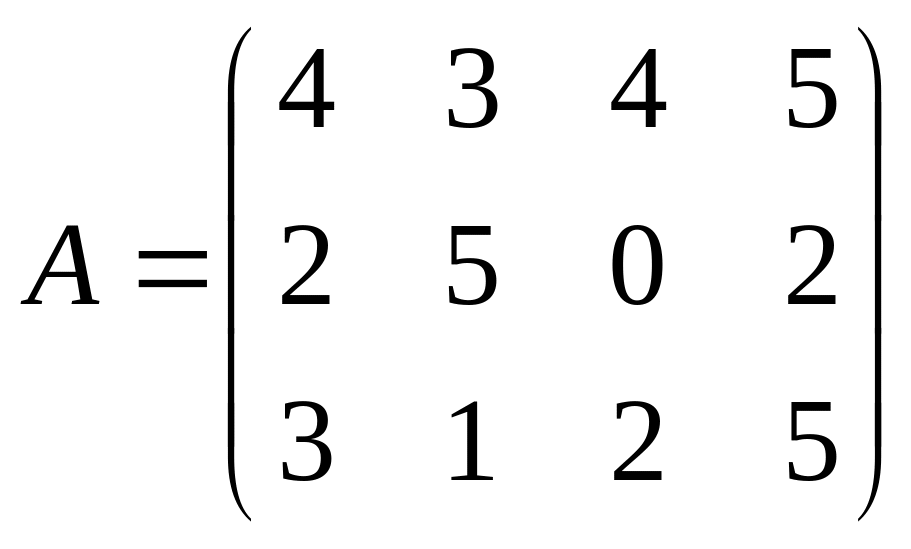
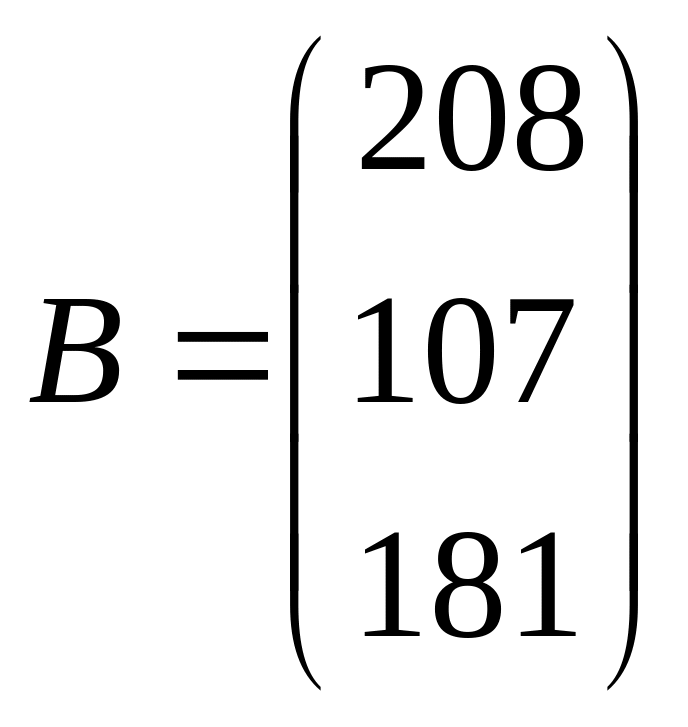
Требуется определить производственную программу, обеспечивающую предприятию наибольшую прибыль при имеющихся ограниченных ресурсах.

Решение.

Для решения данной задачи необходимо составить ее математичкую модель:

найти производственную программу

(x₁, x₂, x₃, x₄)

максимизирующую прибыль

при ограничениях по ресурсам

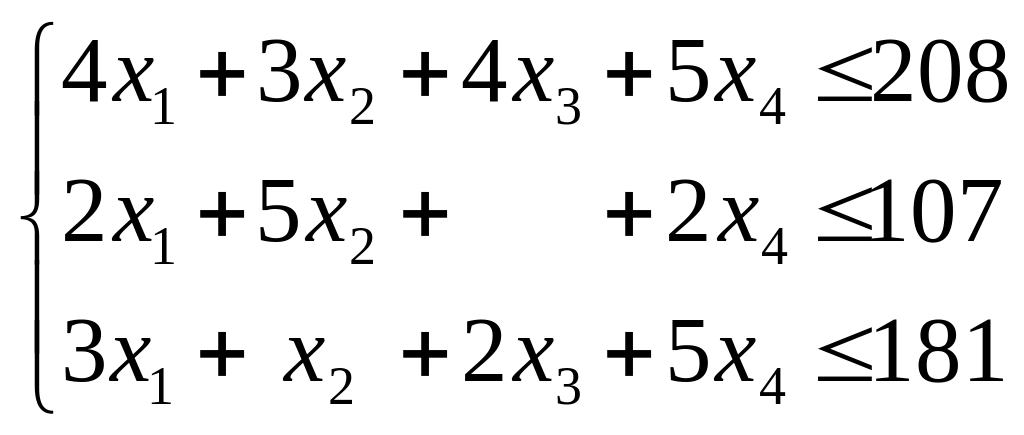
и по смыслу задачи

, , , .

Система ограничений состоит из неравенств. Следовательно, ее необходимо привести к каноническому виду при помощи дополнительных неотрицательных неизвестных x₅, x₆, x₇:

.

Дополнительные переменные x₅, x₆, x₇ имеют смысл остатков соответствующих ресурсов. Среди всех решений системы уравнений, удовлетворяющих условию неотрицательности

, , , , , ,

надо найти то решение, при котором целевая функция примет наибольшее значение.

Базисными неизвестными являются дополнительные переменные x₅, x₆, x₇.

Одним из допустимых решений задачи является базисное неотрицательное решение системы ограничений

Ему соответствует значение целевой функции, равное

.

Для составления первой симплексной таблицы необходимо вычислить :

, , , , , , .