
- •Содержание
- •Введение в теорию принятия решений
- •Тема 1. Теория принятия решений – модель исследования операций
- •1.1. Основные понятия исследования операций
- •1.2. Операционный подход к решению задач
- •1.3. Классификация моделей в исследовании операций
- •Классы операционных задач
- •1. Задачи управления запасами
- •2. Задачи распределения
- •3. Задачи массового обслуживания
- •4. Задачи выбора маршрута
- •5. Задачи замены оборудования
- •6. Задачи упорядочения
- •7. Задачи сетевого планирования и управления
- •8. Состязательные задачи
- •9. Задачи поиска
- •Тема 2. Линейное программирование
- •2.1. Задача линейного программирования
- •2.2. Графический метод решения злп
- •Алгоритм решения задач лп графическим методом
- •2.3. Решение злп симплексным методом
- •1 Симплексная таблица
- •2 Симплексная таблица
- •3 Симплексная таблица
- •4 Симплексная таблица
- •1 Симплексная таблица
- •2 Симплексная таблица
- •3 Симплексная таблица
- •2.4. Теория двойственности в линейном программировании
- •Пример №2.7.
- •2.5. Классическая транспортная задача (ктз)
- •2.6. Общая распределительная задача линейного программирования
2.3. Решение злп симплексным методом
Задача линейного программирования сформулирована как задача минимизации или максимизации линейной формы, переменные которой связаны некоторой системой линейных уравнений и должны быть неотрицательными.
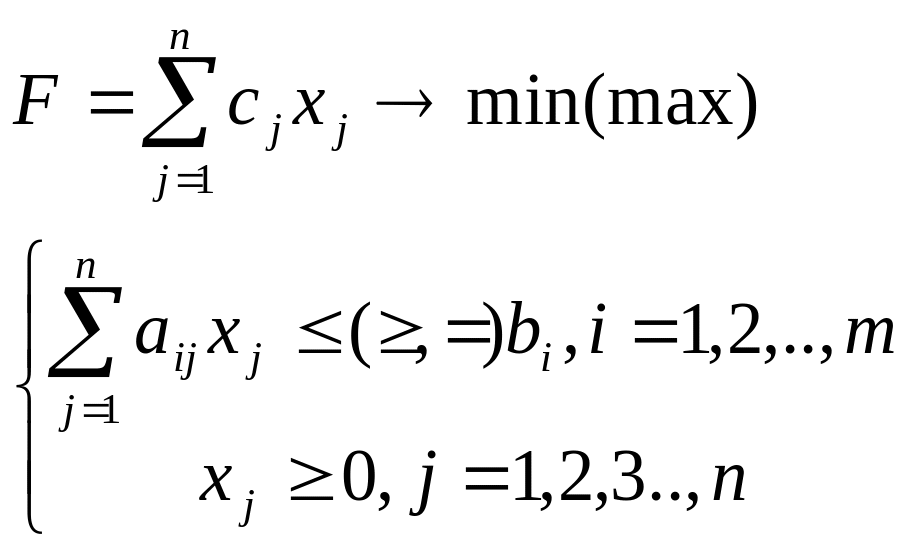
Для решения такой задачи применяется симплексный метод линейного программирования.
Для того чтобы решать ЗЛП симплексным методом необходимо уметь преобразовывать задачу к каноническому виду.
Правила приведения ЗЛП к каноническому виду.
Если требуется найти минимум функции цели F, то заменяя F на (– F) можно перейти к задаче нахождения максимума, т.к. min (F)= -max (-F).
Пример.
Функция цели в стандартной форме:
![]() ,
,
в канонической форме: ![]() .
.
Если условие–ограничение представляет собой неравенство со знаком ≤, то от него можно перейти к равенству, введя в левую часть ограничения дополнительную неотрицательную переменную.
Пример.
Условие ограничение в стандартной
форме: ![]() ,
,
в канонической форме: ![]() ,
,
при этом
![]() .
.
Если условие–ограничение представляет собой неравенство со знаком ≥, то от него можно перейти к равенству, введя в левую часть дополнительную переменную со знаком минус.
Пример.
Условие ограничение в стандартной
форме: ![]() ,
,
в канонической форме: ![]() ,
,
при этом .
Функция цели приводится к каноническому виду путем добавления в нее всех дополнительных переменных, входящих в систему ограничений, с коэффициентом 0.
Пример.
Функция цели в стандартной форме: F=c1x1+c2x2+c3x3+…+cnxn→max(min),
в канонической форме:
![]() .
.
Симплексный метод является методом упорядоченного перебора решений системы ограничений, при условии, что каждое следующее решение улучшает значение функции цели.
Симплексный метод включает в себя 2 этапа:
определение начального допустимого базисного решения системы ограничений и функции цели;
последовательное улучшение начального решения и получение оптимального.
В качестве базисных переменных необходимо выбирать (если возможно) такие m переменных, каждая из которых входит только в одно условие–ограничение с коэффициентом +1 и в остальные n-m условий–ограничений с коэффициентом 0.
Алгоритм симплексного метода.
Шаг 1. Привести систему ограничений и функцию цели к предпочтительному или каноническому виду. Составить матрицу условий-ограничений.
Шаг 2. Определить допустимое решение ЗЛП и вычислить значение целевой функции.
Шаг 3. Составить первую симплексную таблицу.
Шаг 4. Проверить симплексную таблицу на оптимальность.
Шаг 5. Если симплексная таблица оптимальная, то вычисления прекратить. Если нет, то симплексную таблицу необходимо пересчитать по соответствующему алгоритму и составить новую симплексную таблицу.
Шаг 6. Если новая симплексная таблица не содержит оптимального решения, то ее тоже необходимо пересчитать. Пересчет повторять до тех пор, пока не будет найдено оптимальное решение.
Пусть имеется ЗЛП, имеющая предпочитаемый вид (в системе ограничений не содержится неравенств).
Минимизировать или максимизировать
![]() (2.13)
(2.13)
при условиях
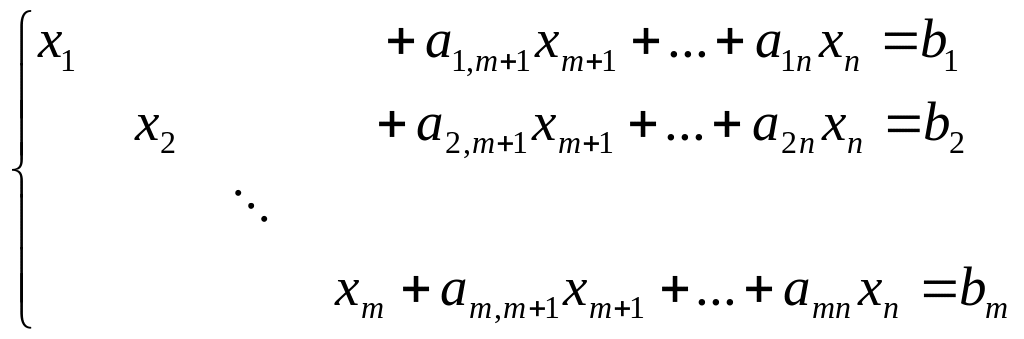 (2.14)
(2.14)
и
![]() ,
,
![]() (2.15)
(2.15)
Шаг 1.
Т.к. задача представлена в предпочитаемом виде, т.е. в системе ограничений нет неравенств, то приводить ее к каноническому виду необязательно.
Для составления матрицы системы ограничений необходимо выписать все коэффициенты системы (2.14) в виде матрицы:
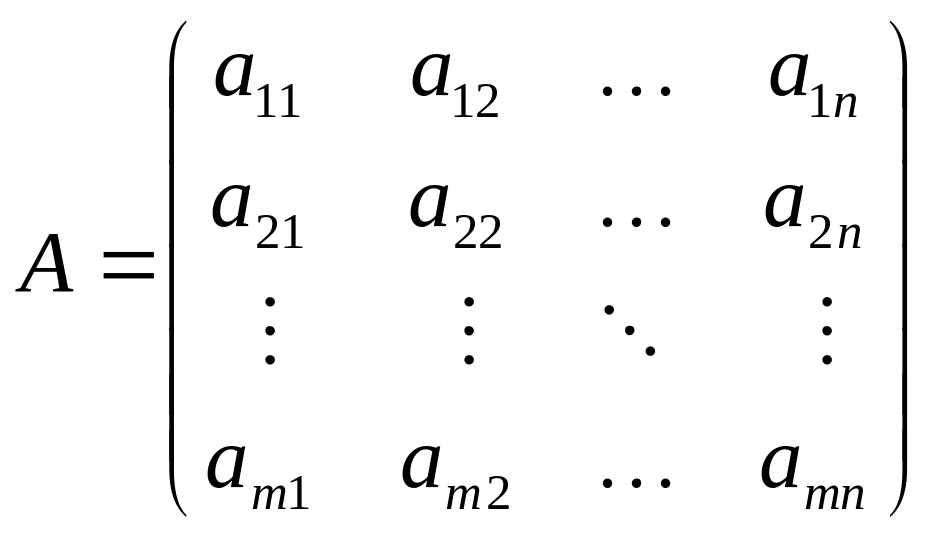 (2.16)
(2.16)
Для удобства решения исходные данные задачи лучше представить в виде матриц значений:
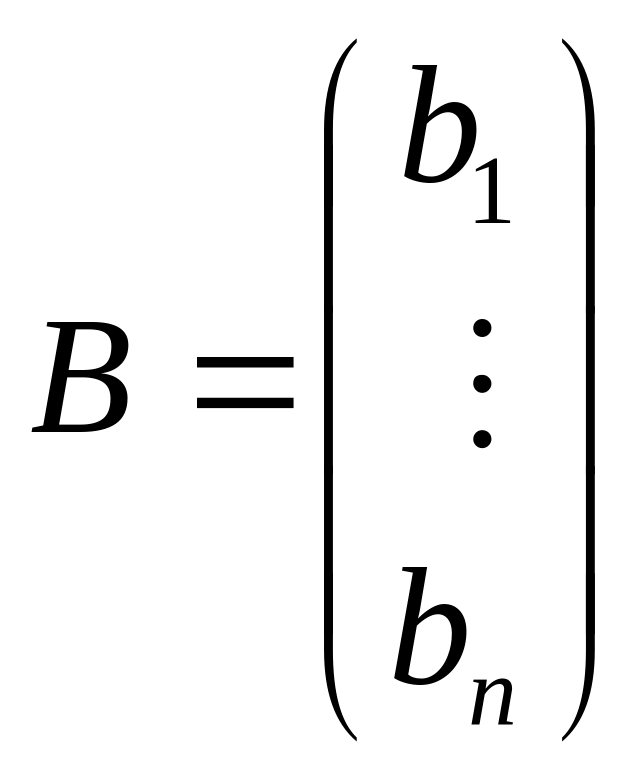
![]()
Шаг 2.
Одним из допустимых решений ЗЛП (2.13) – (2.15) будет базисное неотрицательное решение системы (2.14):
![]() (2.17)
(2.17)
т.к. предполагается, что
![]() ,
i=1,2,…,m.
,
i=1,2,…,m.
Ему соответствует значение целевой функции, равное
![]() .
(2.18)
.
(2.18)
Шаг 3.
Симплексная таблица представляет собой таблицу следующего вида:
Таблица 2.3.
|
Базис |
B |
с1 |
с2 |
… |
сm |
сm+1 |
… |
сj |
… |
сn |
|
|
|
x1 |
x2 |
… |
xm |
xm+1 |
… |
xj |
… |
xn |
с1 |
x1 |
b1 |
1 |
0 |
… |
0 |
a1,m+1 |
… |
a1,j |
… |
a1,n |
с2 |
x2 |
b2 |
0 |
1 |
… |
0 |
a2,m+1 |
… |
a2,j |
… |
a2,n |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
сm |
xm |
bm |
0 |
0 |
… |
1 |
am,m+1 |
… |
am,j |
… |
am,n |
|
|
F0-F |
0 |
0 |
… |
0 |
|
… |
|
… |
|
Основу первой симплексной таблицы составляет матрица системы ограничений (2.16).
В верхней строке данной таблицы вписываются все коэффициенты С линейной формы (2.13).
В первые два столбика заносятся коэффициенты при базисных неизвестные из целевой функции и сами базисные неизвестные.
В третий столбец заносятся свободные члены системы ограничений.
В последней строке записываются
коэффициенты при неизвестных
![]() и свободный член уравнения F0.
и свободный член уравнения F0.
Коэффициенты определяются по формуле:
![]() (2.22)
(2.22)
zj – сумма построчных произведений коэффициентов j-го столбца (j-й переменной) на оценки соответствующих базисных переменных (в симплексной таблице записываются в первом столбце)
![]() ,
,
![]() .
.
Шаг 4.
Для проверки симплексной таблицы на оптимальность необходимо знать следующие правила оптимальности при поиске минимума и максимума функции.
Правила оптимальности для минимизации функции
Правило №1.
Если все коэффициентов , стоящие в последней строке симплексной таблицы по столбцам свободных неизвестных меньше нуля, то найдено оптимальное решение ЗЛП. Функция цели достигает минимума на множестве допустимых решений, т. е. условие оптимальности имеет вид
![]() ,
.
(2.25)
,
.
(2.25)
Правило №2.
Если есть хотя бы одна свободная неизвестная, такая, что коэффициент при ней в последней строке симплексной таблицы положителен и в этом же столбце симплексной таблицы нет ни одного положительного коэффициента, то ЗЛП неразрешима.
Правило №3.
Если есть хотя бы одна свободная неизвестная, такая, что коэффициент при ней в последней строке симплексной таблицы положителен и в этом же столбце симплексной таблицы есть хотя бы один положительный коэффициент, то существует оптимальное решение ЗЛП, для нахождения которого необходимо пересчитать симплексную таблицу по соответствующему алгоритму.
Правила оптимальности для максимизации функции
Правило №1.
Если все коэффициентов , стоящие в последней строке симплексной таблицы по столбцам свободных неизвестных больше нуля, то найдено оптимальное решение ЗЛП. Функция цели достигает максимума на множестве допустимых решений, т. е. условие оптимальности имеет вид
![]() ,
.
(2.25')
,
.
(2.25')
Правило №2.
Если есть хотя бы одна свободная неизвестная, такая, что коэффициент при ней в последней строке симплексной таблицы отрицателен и в этом же столбце симплексной таблицы нет ни одного положительного коэффициента, то ЗЛП неразрешима.
Правило №3.
Если есть хотя бы одна свободная неизвестная, такая, что коэффициент при ней в последней строке симплексной таблицы отрицателен и в этом же столбце симплексной таблицы есть хотя бы один положительный коэффициент, то существует оптимальное решение ЗЛП, для нахождения которого необходимо пересчитать симплексную таблицу по соответствующему алгоритму.
Первую симплексную таблицу еще называют базисным планом.
Шаг 5.
Если не найдено оптимальное решение и выполняется правило №3, то необходимо первую симплексную таблицу пересчитать по соответствующему алгоритму.
Алгоритм пересчета симплексной таблицы
Шаг 1. Выбрать главный столбец симплексной таблицы. Для минимизирующей функции он находится как максимальное среди положительных элементов , стоящих в последней строке таблицы:
![]() (2.26)
(2.26)
Для максимизирующей функции он находится как минимальное среди отрицательных элементов , стоящих в последней строке таблицы:
![]() (2.26')
(2.26')
Шаг 2. Выбрать главную строку. Для этого необходимо произвести построчное деление столбца свободных членов на главный столбец (в делении участвуют только положительные элементы). Главная строка находится как минимальное из найденных частных:
![]() (2.27)
(2.27)
Шаг 3. В новой симплексной таблице на место базисной неизвестной по главной строке поставить переменную по главному столбцу.
Шаг 4. Рассчитать элементы для новой симплексной таблицы, стоящие на месте главной строки:
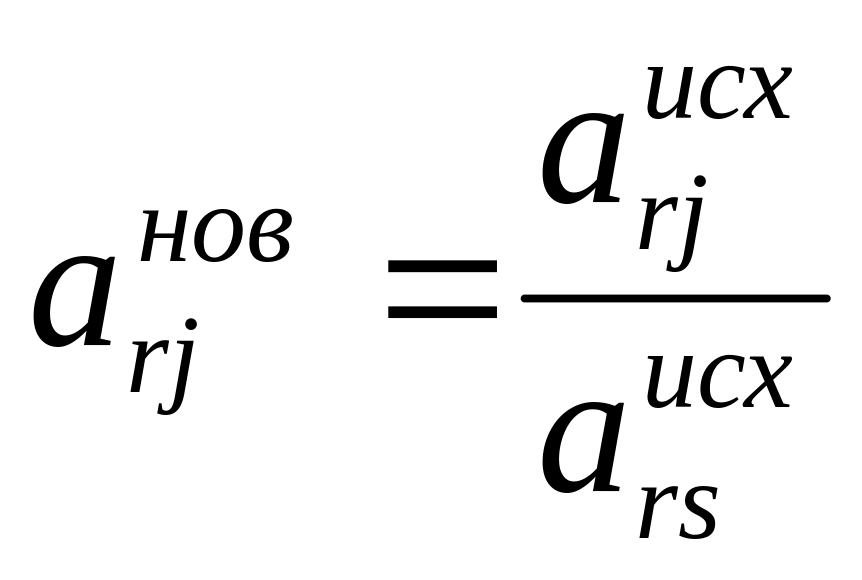 ,
(2.28)
,
(2.28)
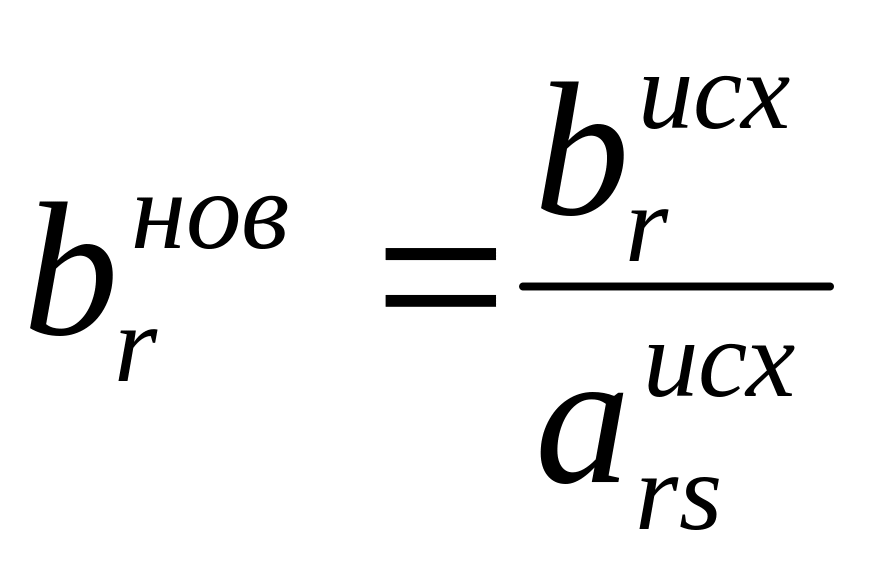 (2.29)
(2.29)
Шаг 5. Рассчитать остальные элементы для новой симплексной таблицы:
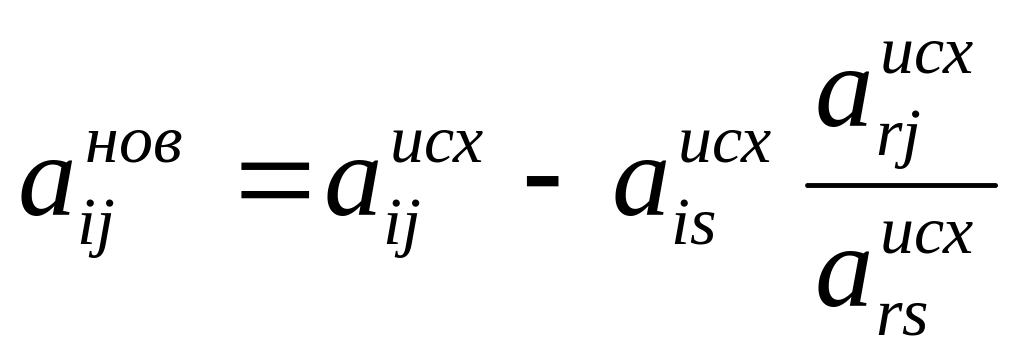 ,
,
![]() ,
(2.30)
,
(2.30)
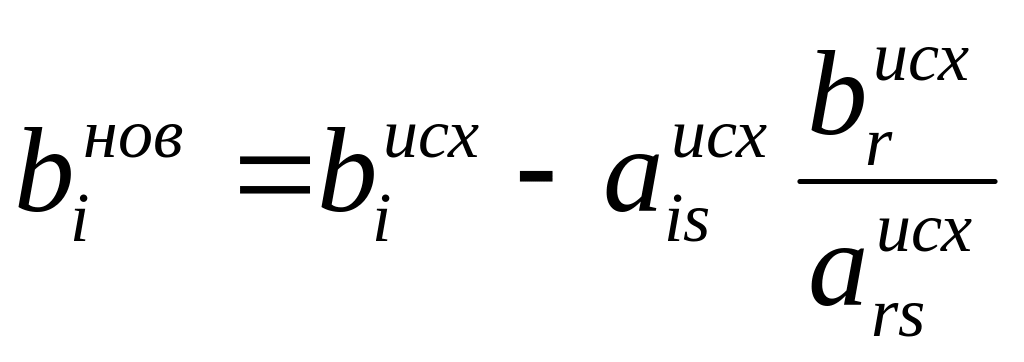 ,
,
![]() ,
(2.31)
,
(2.31)
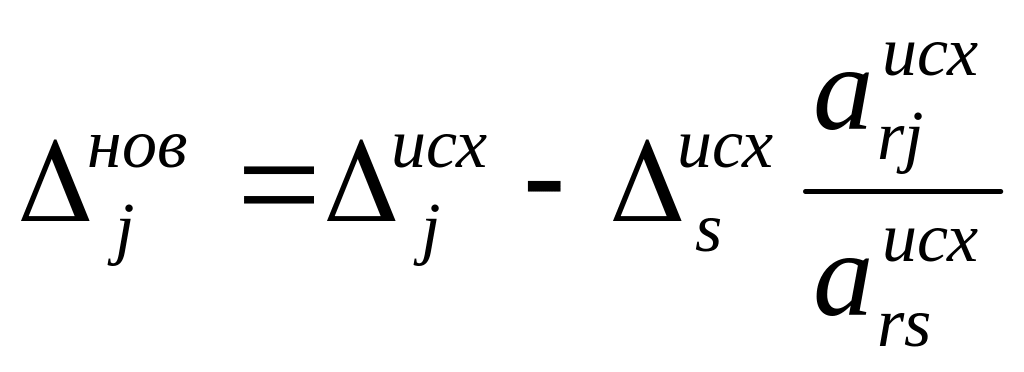 ,
(2.32)
,
(2.32)
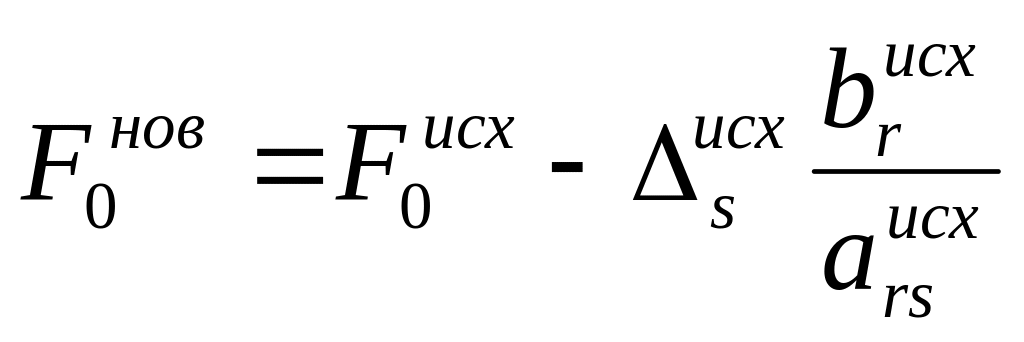 .
(2.33)
.
(2.33)
Шаг 6. В последующих симплексных таблицах первый столбец оценок небазисных переменных исключить.
Процесс перехода к новым решениям продолжается до тех пор, пока не будет получено оптимальное решение.
Пример №2.4.
Минимизировать
![]() ,
(1*)
,
(1*)
при условиях:
![]() (2*)
(2*)
и
![]() (3*)
(3*)
Решение.
Шаг1.
Данную задачу не требуется приводить к каноническому виду, т.к. система ограничений содержит только равенства.
Матрица условий-ограничений для данной задачи будет иметь вид:
![]()
m=2 n=5
Для удобства решения исходные данные задачи следует представить в виде матриц значений:
![]()
![]()
Шаг 2.
В качестве базисных неизвестных выбератся x1 и x2, т.к. каждая из них входит только в одно условие–ограничение с коэффициентом +1 и в остальные условия–ограничения с коэффициентом 0.
Одним из допустимых решений ЗЛП (1*) – (3*) является базисное неотрицательное решение системы (2*)
![]()
Ему соответствует значение целевой функции, равное
![]() .
.
Шаг 3.
определяется по формуле (2.22)
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
![]()
Первая симплексная таблица имеет вид:
