3 Симплексная таблица

Базис	B	x1	x2	x3	x4	x5	x6	x7
x1	27	1	2	2	0	1	0	-1
x6	13	0	3	-12/5	0	-4/5	1	2/5
x4	20	0	-1/5	-4/5	1	-3/5	0	4/5
	1972–F	0	8	7	0	6	0	4

В третьей симплексной таблице среди элементов последней строки нет ни одного отрицательного. Поэтому четвертое базисное решение является оптимальным:

Ответ.

Используя план производства , предприятие получает наибольшую прибыль, равную

.

При этом остаток ресурса первого вида x₅ = 0, второго вида x₆ = 13, третьего вида x₇= 0.

2.4. Теория двойственности в линейном программировании

Задача планирования производства состоит в отыскании такого плана , который позволяет получить максимальную прибыль

(2.34)

при ограничениях по заданным ресурсам

, (2.35)

где по смыслу задачи

, . (2.36)

При этом по оптимальному плану производства некоторые ресурсы используются полностью (назовем их дефицитными), а другие ресурсы избыточны.

В рамках модели ЛП предприятия должна существовать внутренняя система оценки ресурсов, используемых им в процессе производства. Эти оценки связаны с технологическими особенностями (матрицей условий A), со структурой и количеством ресурсов (вектором B), а также со структурой внешних цен (вектор прибылей C). Эти оценки называются расчетными оценками ресурсов.

Пусть имеется другое предприятие – кооператив, который может использовать все имеющиеся у первого предприятия различные виды сырья для выпуска совершенно других изделий по своим технологиям и ставит вопрос о том, чтобы предприятие «уступило» кооперативу имеющееся у них сырье по «договорным» ценам. Как установить эти цены?

Пусть

– оценка единицы i-го вида ресурса;

– вектор оценок ресурсов;

– суммарная оценка всех ресурсов представится.

Естественно, эту сумму кооператоры стремятся минимизировать путем изменения оценок . Со своей стороны предприятие должно учесть, что на производство единицы продукции j-го вида оно должно затратить различные виды ресурсов в количествах и их суммарная оценка будет равна . Очевидно, что имеет смысл «уступить» кооператорам только в том случае, если эта сумма будет не меньше той прибыли, которую получит предприятие от реализации единицы готового изделия.

Таким образом, формулируется новая задача ЛП:

найти вектор оценок ресурсов , минимизирующий суммарную оценку всех ресурсов

(2.37)

при условиях

, , (2.38)

где по смыслу задачи

, . (2.39)

Полученная задача ЛП (2.37) – (2.39) называется двойственной задачей к задаче (2.34) – (2.36). Расчетные оценки ресурсов, соответствующие оптимальному плану производства, служат компонентами оптимального решения двойственной задачи. Поэтому часто компоненту оптимального решения двойственной задачи называют двойственной оценкой i-го ресурса.

Задачи (2.34) – (2.36) и (2.37) – (2.39) образуют пару задач, называемую в линейном программировании двойственной парой.

Сравнивая две сформулированные задачи, видно, что двойственная задача составляется согласно следующим правилам.

1. Целевая функция исходной задачи (2.34) – (2.36) задается на максимум, а целевая функция двойственной (2.37) – (2.39) – на минимум.

2. Матрица

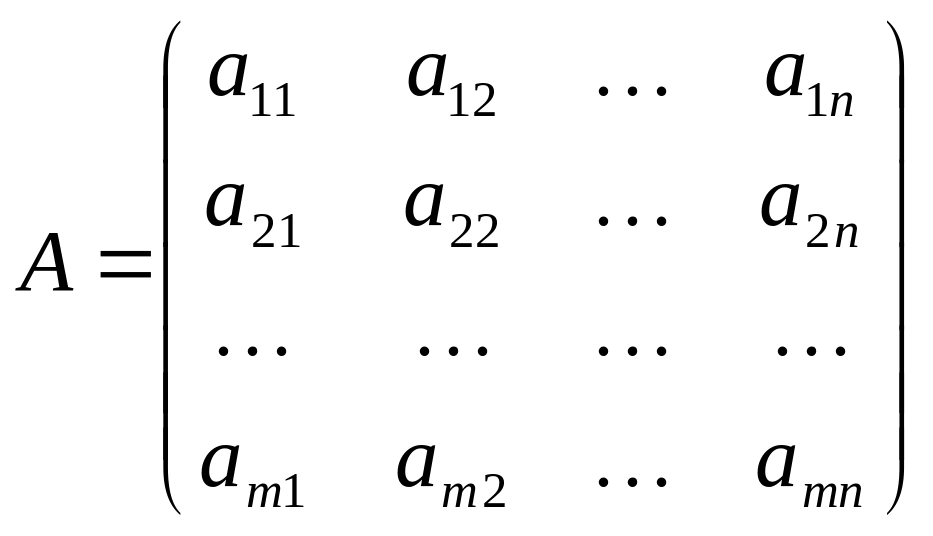(2.40)

составленная из коэффициентов при неизвестных в системе ограничений (2.35) исходной задачи (2.34) – (2.36), и аналогичная матрица

(2.41)

в двойственной задаче (2.37) – (2.39) получаются друг из друга транспонированием (т.е. заменой строк столбцами, а столбцов – строками).

3. Число переменных в двойственной задаче (2.37) – (2.39) равно числу ограничений в системе (2.35) исходной задачи (2.34) – (2.36), а число ограничений в системе (2.38) двойственной задачи – числу переменных в исходной задаче.

4. Коэффициентами при неизвестных в целевой функции (2.37) двойственной задачи (2.37) – (2.39) являются свободные члены в системе (2.35) исходной задачи (2.34) – (2.36), а правыми частями в соотношениях системы (2.38) двойственной задачи – коэффициенты при неизвестных в целевой функции (2.34) исходной задачи.

5. Если переменная x_j исходной задачи (2.34) – (2.36) может принимать только лишь положительные значения, то j–е условие в системе (2.38) двойственной задачи (2.37) – (2.39) является неравенством вида “ 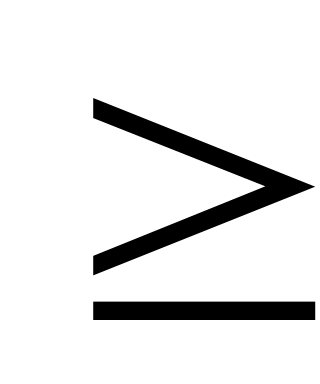”. Если же переменная x_j может принимать как положительные, так и отрицательные значения, то j – соотношение в системе двойственной задачи представляет собой уравнение. Аналогичные связи имеют место между ограничениями (2.35) исходной задачи (2.34) – (2.36) и переменными двойственной задачи (2.37) – (2.39). Если i – соотношение в системе (2.35) исходной задачи является неравенством, то i–я переменная двойственной задачи 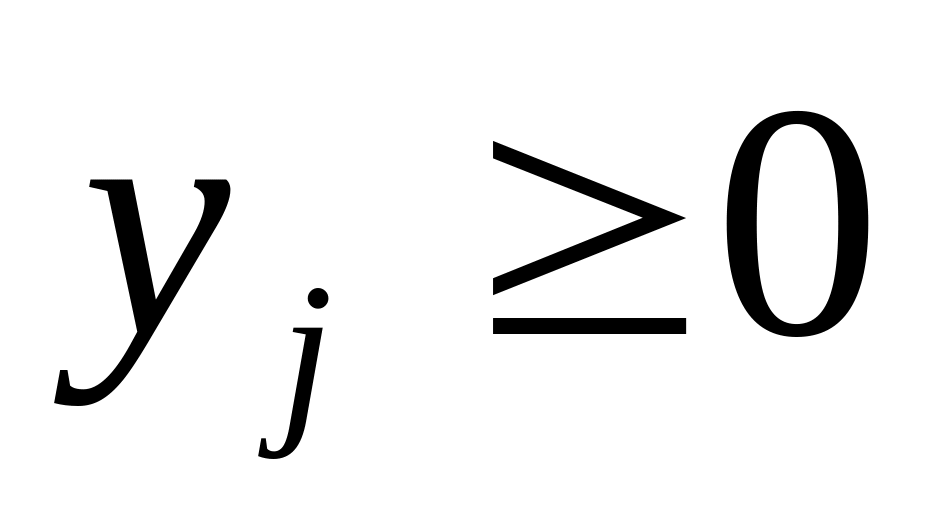. В противном случае переменная у_j может принимать как положительные, так и отрицательные значения.

Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (2.35) прямой задачи и соотношения (2.38) двойственной задачи являются неравенствами вида “ ”. Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.

Для практических целей рассмотренные правила позволяют составить следующую схему соответствия.

Таблица 2.4.

Исходная задача	Двойственная задача
Целевая функция максимизируется	Целевая функция минимизируется
Константы в правых частях ограничений	Коэффициенты целевой функции
Коэффициенты целевой функции	Константы в правых частях ограничений
j-й столбец коэффициентов в ограничениях	j-я строка коэффициентов в ограничениях
j-я строка коэффициентов в ограничениях	j-й столбец коэффициентов в ограничениях
j-я неотрицательная переменная	j-е неравенство вида ≥
j-я переменная, не имеющая ограничений в знаке	j-е соотношение в виде =
i-е неравенство вида ≤	i-я неотрицательная переменная
i-е соотношение в виде =	i-я переменная не имеющая ограничений в знаке

Пример №2.6.

Составить двойственную задачу по отношению к задаче, состоящей в максимизации функции

(1)

при условиях

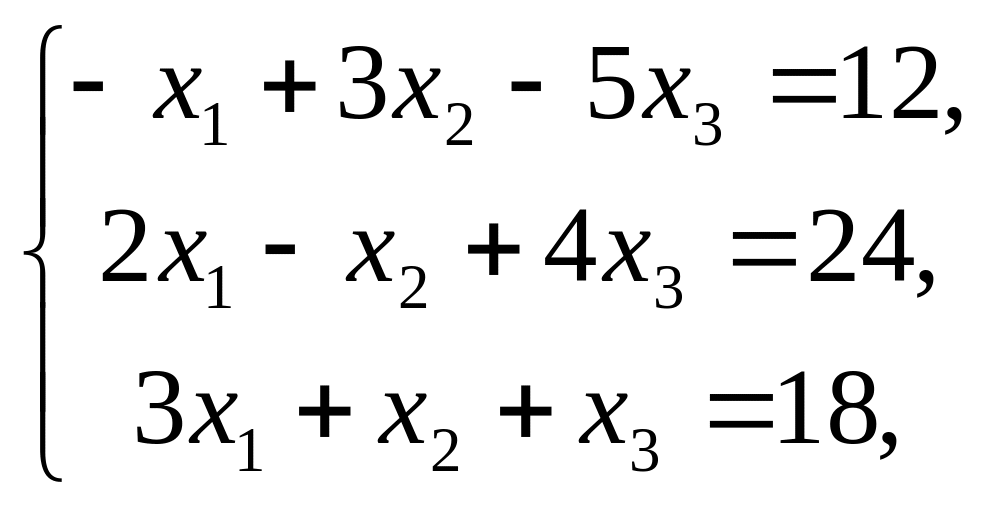(2)

(3)

Решение.

Для данной задач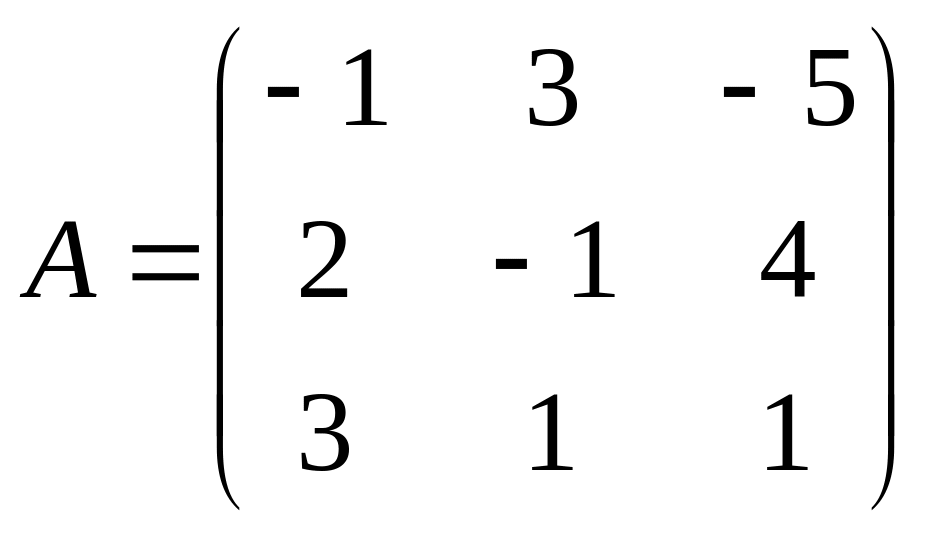и

и .

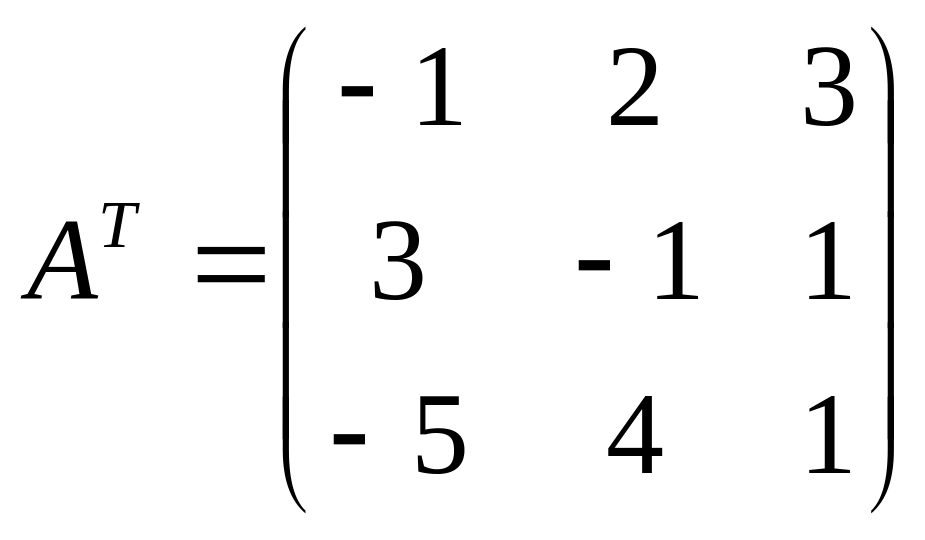Число переменных в двойственной задаче равно числу уравнений в системе (2), т.е. равно трем. Коэффициентами в целевой функции двойственной задачи являются свободные члены системы уравнений (2), т.е. числа 12, 24, 18.

Целевая функция исходной задачи (1) – (3) исследуется на максимум, а система условий (2) содержит только уравнения. Поэтому в двойственной задаче целевая функция исследуется на минимум, а ее переменные могут принимать любые значения (в том числе и отрицательные). Т.к. все три переменные исходной задачи (1) – (3) принимают только лишь неотрицательные значения, то в системе условий двойственной задачи должны быть три неравенства вида “ ”.

Ответ.

Для задачи (1) – (3) двойственная задача имеет вид:

найти минимум функции при условиях

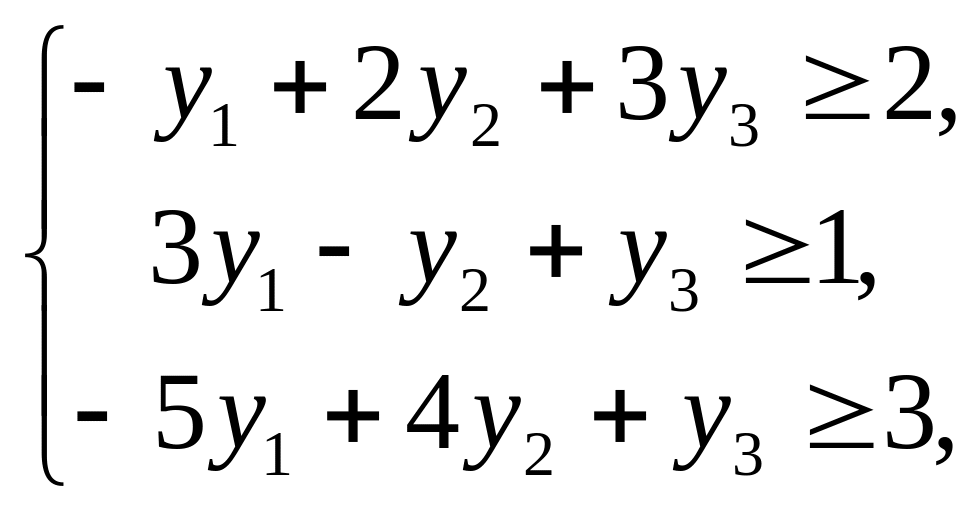
где у₁, у₂, у₃ – любого знака.