Пример №2.7.

Построить двойственную задачу к следующей задаче ЛП:

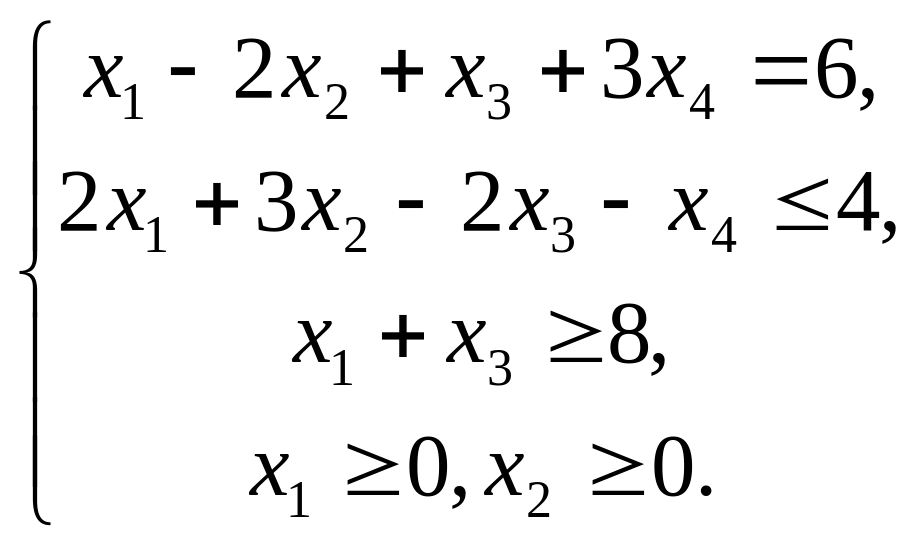
Решение.

Т.к. целевая функция минимизируется, то неравенства должны быть записаны с помощью знака ≥. Поэтому, прежде чем приступать к построению двойственной задачи, необходимо упорядочить запись исходной, умножив второе неравенство на (-1):

.

Теперь, вводя двойственные переменные y₁, y₂, y₃ можно записать в соответствии с указанными правилами пару двойственных задач:

Задача слева – исходная прямая задача, задача справа – двойственная к исходной задаче.

2.5. Классическая транспортная задача (ктз)

В настоящее время задачи транспортного типа или задача прикрепления поставщиков к потребителям стала типовой для промышленных предприятий, имеющих в своем составе несколько фирм, складов, оптовых баз и рынков сбыта. Эти задачи применяются для выбора оптимальных маршрутов доставки продукции от поставщиков к потребителям.

Транспортная задача – это задача о минимизации транспортных расходов, связанных с обеспечением пунктов потребления определенным количеством однородной продукции, производимой (хранимой) в нескольких пунктах производства (хранения).

В общем виде задача может быть сформулирована следующим образом.

Однородный продукт, сосредоточенный в пунктах производства (хранения) в количествах единиц, необходимо распределить между пунктами потребления, которым необходимо соответственно единиц. Стоимость перевозки единицы продукции из i-го пункта отправления в j-й пункт назначения равна c_ij и известна для всех маршрутов. Необходимо составить план перевозок, при котором:

1. запасы всех поставщиков были реализованы;

2. спросы всех потребителей были удовлетворены;

3. суммарные затраты на перевозку были бы минимальными.

Если производство и потребление сбалансированы, т. е. суммарные запасы продукта у поставщиков равны суммарным запросам потребителей:

, (2.42)

то такая транспортная задача называется закрытой или замкнутой. Если же суммарные запасы продукта у поставщиков строго больше или строго меньше, чем суммарные запросы потребителей, то такая задача называется открытой.

Для сведения открытой задачи к закрытой вводятся фиктивные пункты производства или потребления. Если суммарные запасы продукта у поставщиков строго больше, чем суммарные запросы потребителей, вводится фиктивный потребитель, запросы которого равны . Если же суммарные запасы продукта у поставщиков строго больше, чем суммарные запросы потребителей, то вводится фиктивный поставщик, запас продукта у которого равен .

План перевозок, содержащий фиктивные поставки, называется вырожденным.

Пусть

– пункты производства некоторой однородной продукции, ;

– объем производства в пункте ;

– пункты потребления продукции, ;

– потребность в продукции пункта ;

– стоимость перевозки единицы продукции из пункта в любой пункт .

Рисунок 2.5. Транспортная задача.

Математическая модель КТЗ.

Пусть – количество продукции, планируемое к перевозке из пункта А_i в B_j. Тогда, при наличии баланса производства и потребления (2.28) математическая модель транспортной задачи будет выглядеть следующим образом:

найти план перевозок

, где ; ,

минимизирующий общую стоимость всех перевозок

(2.43)

при условии, что из любого пункта производства вывозиться весь продукт

, где (2.44)

и любому потребителю доставляется необходимое количества груза

, где (2.45)

причем, по смыслу задачи

. (2.46)

Здесь целевая функция (2.43) отражает суммарные транспортные расходы. Ограничения (2.44) требуют, чтобы вся продукция была вывезена, а ограничения (2.45) – чтобы потребности всех пунктов потребления были удовлетворены. Условие (2.46) вытекает из физического смысла введенных переменных.

Ограничения (2.44) – (2.46) задают планы перевозок X. Таким образом, математическая модель КТЗ относится к классу задач линейного программирования.

Для решения транспортной задачи чаще всего применяется метод потенциалов. На каждом шаге происходит переход по определенным правилам от одного базисного решения к другому путем заполнения транспортных таблиц. В данной таблице:

1. строки соответствуют поставщикам (в заголовках строк указываются запасы продукта у поставщиков a_i);

2. столбцы соответствуют потребителям (в заголовках столбцов указываются запросы потребителей b_j);

3. в клетки заносятся поставки продукта, перевозимого от соответствующего поставщика к соответствующему потребителю (x_ij);

4. в правом верхнем углу каждой клетки указывается стоимость перевозки единицы продукта от соответствующего поставщика к соответствующему потребителю (c_ij).

Таблица 2.5. Транспортная таблица.

Потребление Производство	b1		b2		…	bn
а1		с11		с12	…		с1n
	x11		x12			x1n
а2		с21		с22	…		с2n
	x21		x22			x2n
. . .	. . .		. . .			. . .
аm		сm1		сm2	…		сmn
	xm1		xm2			xmn

Так как в системе (2.44) – (2.45) ровно (m+n–1) линейно независимых уравнений, то в любой транспортной таблице должно быть m+n–1 занятых клеток.

Алгоритм решения транспортной задачи:

Шаг 1. Привести открытую модель транспортной задачи к закрытой.

Шаг 2. Определить первое допустимое решение по правилу «северо-западного угла».

Правило северо-западного угла.

Заполнение транспортной таблицы начинается с левой верхней клетки («северо-западного угла») и состоит из однотипных шагов, на каждом из которых из рассмотрения исключается один поставщик или один потребитель:

1. если остаток продукта у i-го поставщика после предыдущих шагов меньше, чем неудовлетворенный запрос j-го потребителя, то исключается из рассмотрения i-й поставщик, и в клетку (i, j) заносится поставка x_ij, равная остатку продукта у i-го поставщика после предыдущих шагов;

2. если остаток продукта у i-го поставщика после предыдущих шагов больше, чем неудовлетворенный запрос j-го потребителя, то исключается из рассмотрения j-й потребитель, и в клетку (i, j) заносится поставка x_ij, равная неудовлетворенному запросу j-го потребителя;

3. если остаток продукта у i-го поставщика после предыдущих шагов равен неудовлетворенному запросу j-го потребителя, то исключается из рассмотрения или i-й поставщик, или j-й потребитель, и в клетку (i, j) заносится поставка x_ij, равная остатку продукта у i-го поставщика после предыдущих шагов. В случае исключения i-го поставщика в клетку (i+1, j) заносится поставка x_i+1,j = 0 равная неудовлетворенному запросу j-го потребителя. В случае исключения j-го потребителя в клетку (i, j+1) заносится поставка x_i,j+1 = 0 равная остатку продукта у i-го поставщика после предыдущих шагов.

Шаг 3. Вычислить потенциалы.

1. Каждому поставщику ставится в соответствие потенциал p_i.

2. Каждому потребителю — потенциал q_j.

При этом каждой клетке соответствует некоторая оценка

, (2.47)

где ;

Один из потенциалов можно выбирать произвольно, т.к. в системе (2.44) и (2.45) одно уравнение линейно зависит от остальных. Обычно полагают p₁=0. Остальные потенциалы вычисляются из того условия, что для базисных клеток Δ_ij=0.

Шаг 4. Вычислить оценки всех свободных клеток по формуле (2.47).

Шаг 5. Проверить транспортнцю таблицу на оптимальность:

если среди оценок свободных клеток нет ни одной положительной, то базисное допустимое решение, содержащееся в данной транспортной таблице, является оптимальным.

Шаг 6. Если первая транспортная таблица оптимальная, то вычисления прекраить. Если нет, то транспортную таблицу необходимо пересчитать по соответствующему алгоритму и заполнить новую транспортную таблицу, вычислить новые потенциалы, оценки клеток и т.д.

Шаг 7. Процесс продолжать до тех пор, пока не будет получена транспортная таблица (и соответствующий план перевозок), для которой все

, ; .

Соответствующее последней транспортной таблице базисное решение является оптимальным.

Алгоритм пересчета транспортной таблицы.

Шаг 1. Выбрать свободную клетку (r, s), соответствующую наибольшей положительной оценке

.

Шаг 2. Для выбранной свободной клетки (r, s) построить цикл пересчета – это замкнутая ломаная, одна из вершин которой находится в данной свободной клетке, а все остальные – в занятых клетках, соседние звенья взаимно перпендикулярны, сами звенья параллельны строкам и столбцам таблицы. Цикл пересчета всегда состоит из четного числа вершин.

Шаг 3. Клетку (r, s) пометить знаком «плюс», далее соседние вершины цикла пересчета пометить по очереди знаками «минус», «плюс».

Шаг 4. Из поставок, отмеченных знаком «минус», выбрать минимальную – ρ_max.

Шаг 5. Перейти к новому базисному допустимому решению:

1. к поставкам, отмеченным знаком «плюс», добавляется ρ_max,

2. из поставок отмеченных знаком «минус», вычитается ρ_max.

Пример №2.8.

Однородный продукт, находящийся в трех пунктах производства (m=3), необходимо доставить в четыре пункта потребления (n=4). При этом матрица транспортных затрат на перевозку единицы продукта из любого пункта отправления в любой пункт назначения, вектор объемов запасов продукта в пунктах производства и вектор объемов продукта, необходимых пунктам потребления, имеют вид:

Шаг1. Общий объем продукта в пунктах производства больше, чем требуется всем потребителям , т.е. данная модель транспортной задачи является открытой.

Для того, чтобы превратить открытую модель транспортной задачи в закрытую, необходимо ввести фиктивный пункт потребления с объемом потребления

единиц.

При этом тарифы на перевозку продукта в этот пункт потребления будут равны нулю, т.к. фактического перемещения продукта не происходит.

Шаг 2. По правилу «северо-западного угла» определяется первое допустимое решение:

		30	11	45	36	28
50		30	11	9
70				36	34
30					2	28

Шаг 3. Оценки базисных клеток транспортной таблицы равны нулю.

Приняв , потенциалы вычисляются следующим образом:

Первая транспортная таблица и потенциалы имеют вид:

		30	11	45	36	28
50		30	11	9
70				36	34
30					2	28

Шаг 4. По формуле (2.47) вычисляются оценки всех свободных клеток:

, , ,

, , ,

, .

Шаг 5. Т.к. есть хотя бы одна из оценок свободных клеток строго положительная, то базисное допустимое решение, содержащееся в данной транспортной таблице, не является оптимальным.

Шаг 6. В соответствии с алгоритмом пересчета транспортной таблицы выбирается свободная клетка (r, s), соответствующая наибольшей положительной оценке

Для выбранной свободной клетки (14) строится цикл пересчета: 14-13-23-24.

		30	11	45	36	28
50		30	11	9	*
70				36	34
30					2	28

Клетка (14) помечается знаком «плюс», далее соседние вершины цикла пересчета помечаются по очереди знаками «минус», «плюс». Выбирается минимальная из поставок, отмеченных знаком «минус» , и к поставкам, отмеченным знаком «плюс», добавляется ρ_max, а из поставок отмеченных знаком «минус», вычитается .

Производится перераспределение поставок вдоль цикла пресчета:

9	*					0	9
36	34					45	25

Получается второе базисное допустимое решение. Далее необходимо вычислить новые потенциалы, полагая :

Вторая транспортная таблица и потенциалы имеют вид:

		30	11	45	36	28
50		30	11		9
70			*	45	25
30					2	28

Оценки всех свободных клеток таблицы равны:

, , ,

, , ,

, .

Т.к. есть хотя бы одна из оценок строго положительная, то базисное допустимое решение, содержащееся в данной транспортной таблице, не является оптимальным.

Далее решая задачу по алгоритму получается третье, четвертое, пятое и шестое базисные решения.

Шестая транспортная таблица и потенциалы имеют вид:

		30	11	45	36	28
50		14			36
70		16	11	15		28
30				30

Оценки всех свободных клеток таблицы равны:

, , ,

, ,

, ,

.

Все .

При проверке шестой транспортной таблицы на оптимальность видно, что получена таблица, для которой нет ни одной положительной оценки, следовательно, найдено оптимальное базисное допустимое решение:

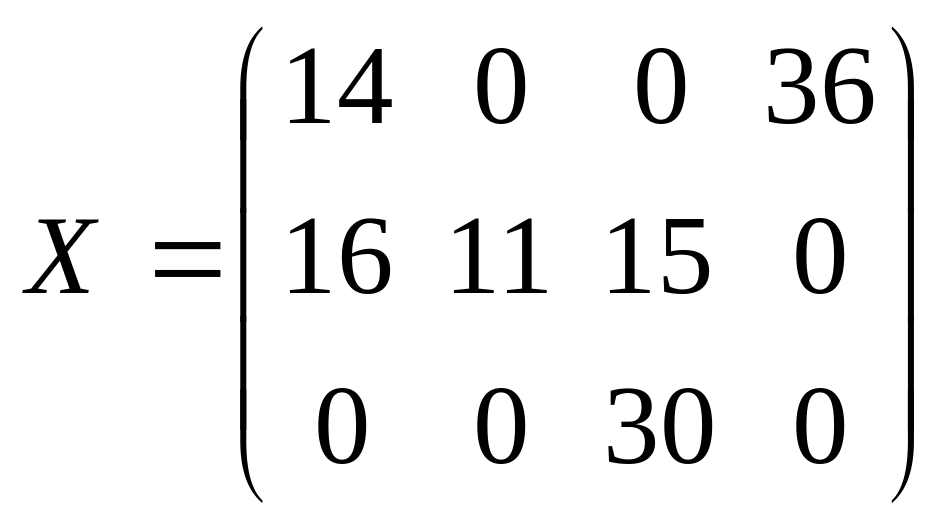
при котором транспортные расходы по обеспечению продуктом всех четырех пуктов потребления будут наименьшими и составят 269 ден.единиц. При этом из второго пункта производства товар будет вывезен не полностью, т.е. там останется остаток продукта 28 единиц.