16. Функциональная полнота систем логических функций. 19. Примеры функционально полных систем

Функционально полная система логических функций представляет собой набор логических функций, с помощью которых можно записать любую, сколь угодно сложную функцию. В этом случае говорят, что этот набор образует базис. Функционально полными являются 3 базиса:

1) "И-ИЛИ-НЕ" (базис конъюнкции, дизъюнкции, инверсии)

2) "И-НЕ" (базис Шеффера)

3) "ИЛИ-НЕ" (базис Пирса или функция Вебба).

Примеры реализации логических операций в базисах “И-НЕ” и “ИЛИ-НЕ”.

Реализация операции “НЕ”:

Реализация операции “И”:

Реализация операции “ИЛИ”:

Пример реализации комбинационного устройства в базисе "И-НЕ". Пусть задана функция, реализуемая комбинационным устройством, в аналитической форме

.

Используя закон де Моргана и с учетом закона двойного инвертирования, запишем эту функцию в виде

.

 

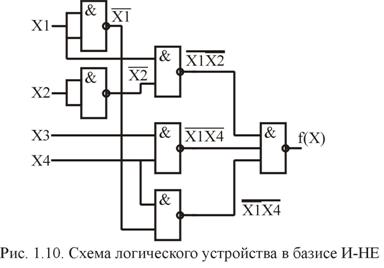
Как следует из полученного аналитического выражения, логическое устройство должно содержать три двухвходовых и один трехвходовой элемент И-НЕ. Функциональная схема комбинационного устройства, построенная в базисе И-НЕ, показана на рис. 1.10.

20. Основные понятия исчисления предикатов.

Решение многих задач обработки информации требует ее логического анализа. Для автоматизации логического рассуждения необходим некоторый формальный язык, на котором можно формулировать посылки и делать логические выводы. Такой язык имеется. Он носит название языка логики предикатов.

В математике, информатике, кибернетике и других науках наряду с высказываниями встречаются выражения, грамматически имеющие форму высказываний, но содержащие предметные переменные некоторых множеств, а не конкретные объекты этих множеств. Здесь под предметными переменными понимаются произвольные, неконкретизированные объекты указанных множеств. Такие выражения можно получить из любых высказываний, заменив в них обозначения предметов предметными переменными множеств, к которым принадлежат эти предметы. Если в последних выражениях все предметные переменные снова заменить какими-либо элементами данных множеств (необязательно исходными), то опять получим высказывания.

Исчисление предикатов - это такая логическая система, с помощью которой можно выразить большую часть знаний, относящихся к математике, математической лингвистике, естественным разговорным языком. Эта система содержит правила логического вывода, позволяющие делать верные логические построения новых утверждений, исходя из некоторого заданного множества утверждений. Благодаря своей общности исчисление предикатов может претендовать на использование для компьютерного построения умозаключений.

Например,

“2 – простое число” - высказывание;      “3>1” - высказывание.

Но, заменив числа в этих высказываниях предметной переменной n из множества натуральных чисел, получим выражения:

“n - простое число”,      “n₁>n₂”, являющиеся не высказываниями, а предикатами. Предикаты отражают свойства и отношения между предметами из предметной области.      Обозначим

P₁(n) - свойство “быть простым числом”, а      P₂(n₁,n₂) отношение “n₁ больше n₂”.

В общем случае мы ничего не можем сказать о значении предиката, но подставив, например, в P₁ и P₂ значения n=2, n₁=3, n₂=1, получим

P₁(2) - “2-простое число”,      P₂(3,1) - “3 больше 1” -

истинные высказывания, а подставив значения n=4, n₁=1, n₂=3. получим

P₁(4) - “4 – простое число”,      P₂(1,3) - “1 больше 3” –

ложные высказывания, т.е. предикат при подстановки конкретных констант из предметной области, может принимать значение И или Л.

 =========================================================