45. Построение графа наименьшей длины

Большое практическое значение имеет следующая задача, которую можно сформулировать в виде задачи о проведении дорог. Имеется несколько городов а, Ь, с ..., которые нужно соединить между собой сетью дорог. Для каждой пары городов (х, у) известна стоимость 1(х, у)' строительства соединяющей их дороги. Задача состоит в том, чтобы построить самую дешевую из возможных сетей дорог. Вместо сети дорог можно рассматривать сеть линий электропередачи, сеть нефтепроводов и т. п. Называя в графе, изображающем сеть дорог, величину 1(х, у) длиной ребра (х, у), приходим к задаче о построении графа наименьшей длины. Поэтому далее в качестве стоимости дорог примем длину ребер графа.

Если имеются всего три вершины (а, Ь, с), то достаточно построить одну из соединяющих цепей аЬс, асЬ, Ъас, причем еслиbe-самое длинное ребро, то именно его и надо исключить, построив цепь Ъас.

Граф наименьшей длины всегда является деревом, так как если бы он содержал цикл, можно было бы удалить одно из ребер этого цикла и вершины все еще остались бы соединенными. Следовательно, для соединения п вершин нужно построить п-1 ребро.

Покажем, что граф наименьшей длины можно построить, пользуясь следующим правилом. Прежде всего соединяем две вершины с наиболее коротким ребром ui. На каждом из следующих шагов добавляем самое короткое из ребер u1;, при присоединении которого к уже имеющимся ребрам не образуется никакого цикла. Если имеется несколько ребер одинаковой длины, то выбираем любое из них. Каждое деревоQ, построенное таким образом, будем называть экономическим деревом. Его длина равна сумме длин отдельных ребер:

l(Q)= . (3.13)

Покажем, что никакое другое дерево, соединяющее те же вершины, не может иметь длину, меньшую длины экономического дереваQ. Пусть Р--дерево наименьшей длины, соединяющее рассматриваемые вершины, аQ - любое экономическое дерево. Предположим, что ребра U1,U2..Un-i занумерованы 'в том порядке, в котором

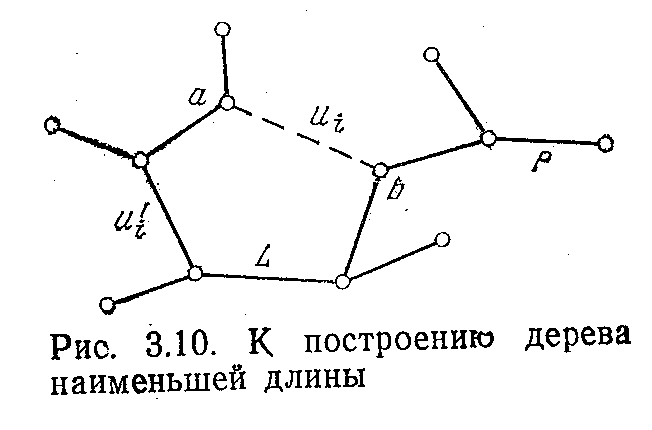
Рисунок 10 - К построению дерева наименьшей длины

они присоединялись при построении Q, т. е. удовлетворяют условию l(uk) .l(uk+1) Если дерево Р не совпадает с Q, то Q имеет по меньшей мере одно ребро не принадлежащее Р. Пусть ui=(a, b)-первое таке ( ребро и пустьL(a, b)-цепь графа Р, соединяющая вершины и и b, как, например, на рис3.10. Если ребро u1 добавить к Р, то получим цикл, а так как Q не имеет циклов, то в этот цикл должно входить по крайней мере одно ребро, не принадлежащее Q. Пусть это будет u'i. Удалив его, получим дерево Р' с тем же числом вершин, что и Р, длина которого

1(Р')=1(Р)+1(ui)-1(и'i). (3.14)

Так как граф Р имеет наименьшую длину, то l(Ui) l(u'i). ;(3.15)

Но Ui было ребром наименьшей длины, при добавлении которого к ребрами1, и2...,ui-1 -не получается циклов. Так как при добавлении и''-i к этим ребрам также не получается никакого цикла, то

l(u1)=l(ui) (3.16)

и, следовательно, Р' имеет, так же как и Р, наименьшую длину. Но Р' имеет с экономическим деревом Q на одно общее ребро больше, чем Р. Повторяя эту операцию несколько раз, получаем дерево наименьшей длины, совпадающее с Q. Следовательно, Q-дерево наименьшей длины..