37. Методика изучения признаков параллельности прямых
Определенные затруднения учащиеся испытывают при изучении теорем, формулировки которых имеют сложное логическое строение. Задача: если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны. Необходимо иметь в виду, что здесь сформулированы две теоремы: 1) ёсли внутренние накрест лежащие углы равны, то прямые параллельны; 2) если сумма внутренних односторонних углов равна 180°, то прямые параллельны. Методическая схема изучения признаков параллельности прямых может быть такой: 1) подвести учащихся к теореме и сформулировать ее; 2) сообщить идею и план доказательства; 3) провести доказательство по плану, закрепить каждый этап (переход к следующему этапу доказательства осуществляется после закрепления предыдущего); 4) закрепить доказательство путем его полного воспроизведения; 5) применить теорему к решению задач. Для изучения данной теоремы и ее док-ва предлагается репродуктивный метод обучения с элементами эвристической беседы.
52
53
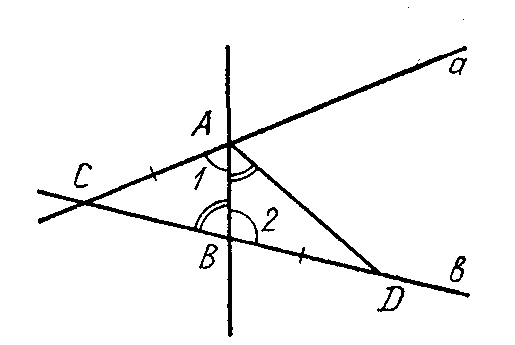54
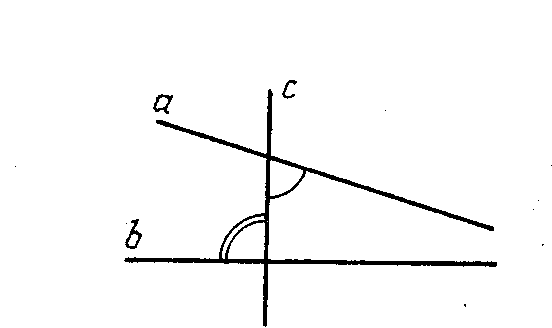
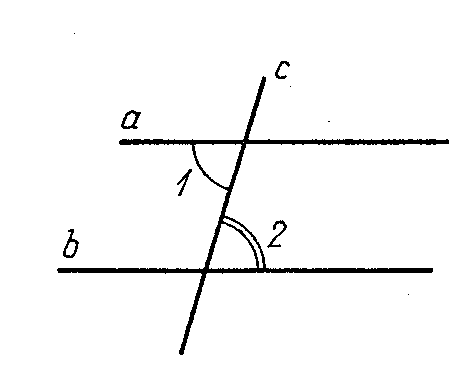
1.Подведение к теореме. Предлагаем учащимся рассмотреть два рисунка (рис. 52, 53). Вопросы: «Назовите внутренние накрест лежащие углы на этих рисунках», «Сравните накрест лежащие углы на первом рисунке. Равны они или не равны?», «Как располагаются прямые а и b? Параллельны они или пересекаются?», «Сравните накрест лежащие углы на втором рисунке. Равны они или не равны?», «Как располагаются прямые а и b в этом случае? Параллельны они или пересекаются?», «При каком условии прямые а и b параллельны? На основе проведенного наблюдения формулируется теорема: «Если накрест лежащие углы равны, то прямые параллельны». Выясняется, что дано в этой теореме (условие), а что нужно доказать (заключение). Делается краткая запись теоремы:
Дано: угол1 и угол 2— накрест лежащие, угол 1 = угол 2 (см. рис. 53).
Доказать: а||b.
2. Идея док-ва. Док-во будем проводить методом от противного. Для этого необходимо допустить, что прямые а и b пересекаются. В результате получится треугольник АВС (рис. 54). Док-во опирается на построение еще одного треугольника ВАD и сравнение его с треугольником АВС.
3. План доказательства:
1) а и b пересекаются (допущение);
2) ∆ВАD;
3) ∆ВАD=∆AВС;
4) уголDАВ=уголАВС;
5) уголDВА = уголВАС;
6) противоречие: уголСВА + уголDВА = 180°, уголDAB+уголCAB<180°;
7) а||b. ч.т.д.
(не надо)
4. Осуществление плана доказательства. Итак, делаем допущение, что прямые а и b не параллельны и, следовательно, они пересекаются. Пусть С — точка пересечения этих прямых. Получаем треугольник АВС.
Воспользуемся далее методом беседы (если детализация беседы не окажется необходимой, она может быть проведена в более свернутом виде).
39. Метод площадей. Теорема Пифагора
В разделах курса планиметрии понятии многоугольника трактуется не одинаково. В одних их многоуг А1А2…Аn - это фигура, состоящая из отр А1А2, … Аn-1Аn любые два из которых, имеющие общий коне, не лежат на одной прямой (Погорелов, атоносян). В этом случае при рассм площади многоуг под кажд из них понимается соотв плоский многоуг (конечная часть плоскости, ограниченной многоуг). В др (Гваздович, Латотин) многоуг – часть пл, ограниченной простой замкунтой ломанной, вместе с этой ломанной (простая ломанная – не имеет самопресечений).
Частные случаи многоуг – 4уг – это традицион для курса планиметрии материал. Из всевозможных 4-ков выделяют для подробного изуч выпуклые. (если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону). Во всех действующих в н.вр. пособиях осущ. Один. Подход в введении частных видов парал-ма – прямоуг, ромб. Что касается квадрата, то, напр, в уч. Александрова, он вводится как 4-ник, кот. Одновременно явл прямоуг и ромб, а в др. он определ. как частный вид прямоугольника (Погорелов, Атоносян)
Все определения указ 4-ков даётся через родовое и видовое отличие(прямоуг – парал-мм, у кот все углы прямые). Род вид отличиетрапеция рассматривается после парал-ма и его частных случ.
При рассм. Разл св-в и признаков парал-ма широко исп св-вва и признаки равных 3-ков, св-ва углов, образов при пересечении двух прал-ных прямых третьей, признаки прал-сти прямых
Материал о прал-мме и его частн видах очень удобен для р-тия логич мышления уч-ся. Именно здесь учит имеет широкие возможности по работе с определен (м-о предложить ученикам дать сам-но опред прямоуг через понятия 4-ка вообще «это 4к, у кот все углы прямые»), можно организ изучение темы так, что при min-ной помощи учит-я уч-ся сам-но смогут выявить и док-ть св-ва и признаки прал-мма, трапеции. Напр, 1) посмотрим на парал-мм АВСД, О – т. пресеч диагоналей. Какие особенности пал-мма вы замеч, кроме прал-сти противоположных сторон? 2) учен – противопол стороны равны, противопол углы равны 3) давайте д-жем, что противопол стороны равны, при этом будем использовать предыд. Теоремы. Как вы думаете, какие из них м использ? 4) подвести учен к выводу или напомнить им, что до сих пор мы исп признаки рав-ва треуг, прал-сти пр, возможно, здесь также их надо исп? 5) как д-ть рав-во сторон АВ и СД? Какие 3-ники здесь можно исп? 6) учен – 3-ники АВО и СОД 7) что можно сказать о этих 3-ках? Можно ли сказать, что они равны? 8) уч – из рис – они равны 9) если мы докажем, что эти 3-ники равны, то их соотв стороны будут равны. В т.ч. сторны АВ и СД. Какой признак рав-ва 3-ков надо использ-ть, чтобы д-ть рав-во этих 3-ков? 10) далее самост доказ-во 11) в том же плане можно организ. рассмотр-е других св-в 4-ков (прямоуг, ромба, квадрата, трапеции) св-ва и призн. 4-ков разных видов нах широкое примен-е при изуч многогр-ков и тел вращения.
Методика введен. понятия пл-ди. Значит место в школьной мат-ке занимают вопросы измерения геом. Величин (длин, площадей, объёмов). Измерение геом величин тесно св с идеей аксиоматич метода, теорией действит чисел, методами матем анализа. При изуч дан вопроса уч-ся знакомятся целым рядом формул, с пом кот расширяются возможности применения в шк курсе геом аналит метода.
Понятие площади в курсе планиметрии традиц ввод в 8-9 кл. При чём, в начале рассм понятия площади многуг-ка (простой фигуры), а в последствии – понятие площади круга.
В уч Атоносяна площадь мног-ка опред как величина части плоскости, кот занимает мног-к, и далее формулир св-ва этой величины. В уч Погорелова – площадь выступает как частный случай понятия площади простой фигуры (под простой ф понимается геом ф, кот м разбить на конечное число плоских 3-ков, где под плоским 3-ком понимается ч пл, ограничен 3-ком), для кот фор-ся св-ва, аналогичные тем, кот сформулир для площади мног-ка в уч атоносяна. Это: площадь простой фигуры – это положит величина, численное знчение кот обладает след св-ми: 1. равные ф имеют равные площ 2. если ф разбиваются на части, явл-ся простыми фигурами, то площадь ф = сумме площадей её частей 3. площадь квадрата со стороной 1 = 1(В уч Атоносяна – площадь квадрата = квадрату его стороны)
Указан св-ва пл-ди исп в обоих уч для док-ва Т. о площади прямоуг, прал-мма, 3-ка, трапеции
Н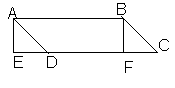
апр,
площаль парал-мма 1.
рассм АВСД – прал-мм и путем дополнит
построения сравниваем его с прямоуг
АЕFВ
2.
прямоуг 3-ки АЕД и ВFС
=, зн. их площади =. 3.
дан прал-мм и прямоуг, имеющие =ые площади,
т.к. они разбиваются на равные части 4.
значит площадь парл-мма = площади прямоуг
= ВЕ·FC=BF·ДС
Кроме понятия площади простой фигуры (мног-ка) в курсе планиметрии учебника Погорелова даётся представление о площади произваольной фигуры, формулир след определ: «данная фигура имеет площадь S, если сущ содержащие её простые фигуры, т.е. мног-ки, и содержащиеся в ней простые ф, с площадями как угодно мало отлич от S» Это определ примен в уч Погорелова к нах площади круга. В уч Атоносяна т опред не формулир, а ф-ла площали круга выводится почти аналогично как у Погорелова.