35. Функциональная линия

Ф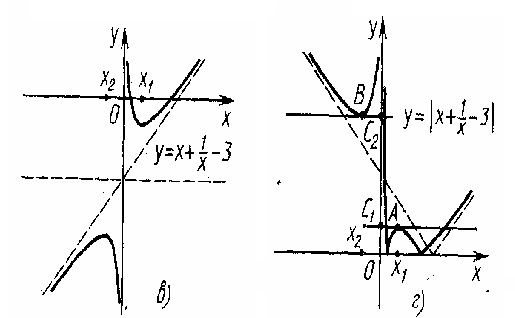 ункциональная линия шк-го курса матем-ки явл. в настоящее время одной из ведущих, определ-х стиль изучен. многих тем и разделов курсов алг-ры и начал анал. Наибол. заметной особенн-тью материала этой линии явл. то, что с его помощью возможно устанавливать разнообразные связи в обучении. В кач-ве прим., на кот. рассм-м некот. важные особенн. этой линии, разберем след. задание:

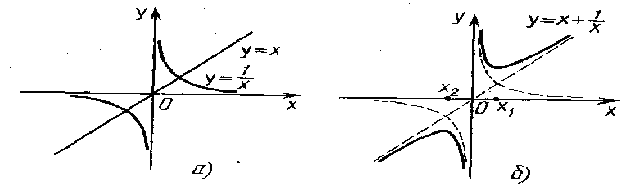
Пример 1. При каких значениях параметра а уравнение |х+1/х-3| =а имеет ровно четыре корня?

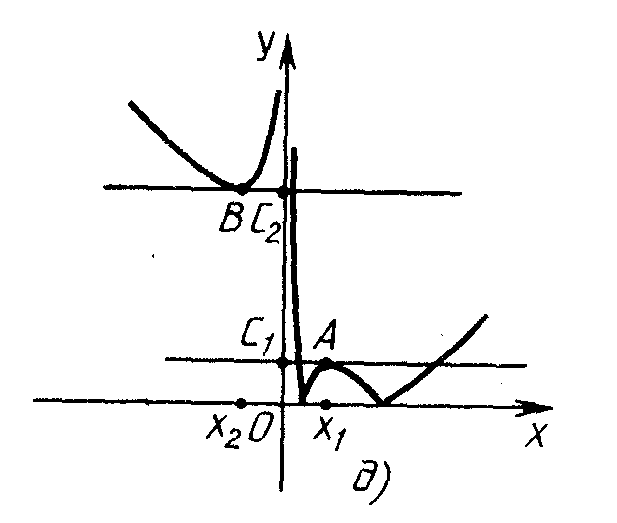
Реш-е. Постр. гр-к фун-ии с(х)= |х+1/х-3|. Различн. этапы построения гр-ка показаны на рис. а–г. На рис. д показ. некот. точки, использ-е для иссле-ий, они появл-я в процессе построен.

Найдем число точек пересечения графика фун-ии с(х) (обозначим его Г) и прямой l с уравнением у=а. На рис. д видно, что 1 пересекает Г в 4 точках в том случае, когда 1 распол. в верхней полуплоскости и не пересекает отрезок [с1, с2]. Первое из этих условий приводит к ограничению a>0. Для нахождения второго заметим, что точка на оси абсцисс с координатой х1 - точка max фун-ии с(х) на отрезке [а1, а2], аналог. х2 точка min ф-ции с(х) на интервале ]-∞, 0[. Числ-е значен. для х1 и х2 можно получить, учитывая, что нер-во | x+1/x|>= 2 справедливо х обращается в равенство только при х =1 и х= -1. => с1=1, с2=5. => 4 корня данное ур-ние имеет при а[0; 1]U[5; ∞].

Как легко заметить, основа приведенного решения состоит в использовании функциональных и графических представлений. Принципиально решение состоит в переходе от исследования данного уравнения к исследованию графика функции с(х). Однако наиболее трудная часть решения в данном случае состоит в построении графика функции с(х). Рассмотрим основные этапы построения.

На рис. а изображены графики исходных для с(х) ф-ций y=1 и у=1/x. Это простейшие элементарные функции. Они входят в состав определенных классов элементарных функций и подробно изучаются в своем классе. Рисунок б показ. график сумы этих ф-ций. Как это ни удивительно на первый взгляд, график ф-ции у=х+1/x школьными средствами построить с достаточной точностью почти невозможно. Причина состоит в том, что в этом курсе отсутств. операции с фун-ми, такие, как сложен. Не дается поэтому и представл-е о построен. граф-в суммы двух ф-ций, так что в каждом случае такой график приходится строить, пользуясь особенн-тями данного выражения. Здесь можно рассуждать так:

при больших по абсолютному значению аргументах х+1/х приблиз рав x, а

при малых х+1/х приблиз рав 1/x так что график функции у= х+1/х близок соответственно к биссектрисе 1—III координатных углов и гиперболе у=1/х. Здесь же на основе тождества | x+1/x|>= 2 могут быть указаны точки х1 и х2. На рисунке в, г показано, как график последовательно подвергается действию параллельного переноса вдоль оси ординат и симметрии относительно оси абсцисс. Эти преобразования графиков рассматриваются в курсе алгебры: первое — при построении графика функции f(х)+с по графику функции f(х), второе — при построении графика функции |f(х)| по графику функции f(х); соответствующие задания устанавливают связи курсов алгебры и геометрии на основе координатного метода. Наконец, интерпретация данных использует принцип:

ур-ние с(х)=а имеет столько же корней, сколько имеет точек пересеч-я гр-к ф-ции у=с(х) и прямая с ур-м у=а. На этом этапе изучение графика сочетается с числовыми расчетами: график позволяет найти точки, значен. координат которых позволят найти ответ, а использ-е нер-в приводит к их определению.

Поскольку метод, с помощью которого была решена задача, состоял в преобразовании исходного задания, построении для него более удобной модели, причем основным инструментом здесь явились понятия функции и графика функции, естественно назвать этот метод методом функционально-графического моделирования. Освоению этого метода и с формальной, и с прикладной стороны в значительной мере подчинено изучение всей функциональной линии курсов алгебры и начал анализа.

Связующая роль функциональной линии достаточно полно отражена в методическом анализе решения примера; отметим только, что при рассмотрении заданий, связанных с построением графиков функций, можно организовать работу по пропедевтике ряда понятий математического анализа уже в курсе школьной алгебры; в данном примере, в частности, особую роль играли экстремальные точки функции c(х), и при разборе решения примера можно указать на их значение.

Разобранный пример значительно превышает по сложности те задания, которые посильны учащимся даже на заключительных этапах изучения курса алгебры. Вместе с тем он дает представление о тех трудностях, которые учащиеся будут испытывать при освоении метода функционально-графического моделирования, поскольку идеи, собранные в решении примера, присутствуют и в более простых заданиях, имеющихся в содержании обучения.