25. Различные трактовки понятия функции.

Понятие ф. введено в м-ку в конце 17 ст. (впервые Р.Декарт исследовал, как изменяется ордината точки с изменением ее абсциссы, термин функция в 1694 г.- ввел Г. Лейбниц).

1)Величина У наз.функцией переменной величины х в области определения D, если каждому значению х из этой области соответствует одно определенное значение величины У (классическое определение)

2) Отношение между мно-вом X и мн-вом У, при котором каждому элементу мн-ва X соот-ет не более одного эл-та мн-ва Y наз. функцией (пo Н.Бурбаки).

27. Равносильные и неравносильные пр-я уравнений и н-в. Причины появления "посторонних корней" ур-ний. Потеря корней уравнений.

Посторонний корень (математический), корень (решение) одного из промежуточных уравнений (т. е. получающихся в процессе решения данного уравнения), не являющийся корнем этого данного уравнения. Появление П. к. связано с тем, что при решении не всегда удаётся, упрощая данное уравнение, совершать переходы только к равносильным уравнениям. П. к. могут появляться, например, при возведении обеих частей уравнения в степень, при освобождении от знаменателя, при потенцировании и т.п. Пример: уравнение log₂(x — 5) + log₂(x — 3) = 3 имеет только один корень х = 7; однако после потенцирования получается уравнение (х — 5)(х —3) = 8, имеющее, помимо корня х = 7, также корень х = 1, являющийся П. к. для исходного уравнения.

Причина появления посторонних корней.

Решение иррациональных уравнений основано на следующем утверждении:

Из теоремы следует, что если в ходе решения иррационального уравнения приходилось возводить обе части в степень с четным показателем. Но могут появиться посторонние корни уравнения, т.е. корни уравнения А(х)=В(х).

Итак, что же происходит, каковы причины посторонних корней:

а) за счет возможного расширения ОДЗ исходного уравнения (т.е. ОДЗ полученного уравнения шире ОДЗ исходного уравнения).

б) за счет возведения в четную степень его левой и правой частей, которые равны по абсолютной величине, но одна из них положительна, а другая отрицательна.

Проверка корней.

Чтобы отделить посторонние корни, не всегда необходимо подставлять найденные корни в данное уравнение. Рассмотрим два вида уравнений:

 

       

   Ответ: 3

     Ответ: 2

31.СПОСОБЫ РЕШЕНИЯ УРАВНЕНИЙ И НЕРАВЕНСТВ В ШКОЛЕ.

Обзор методов уравнений и неравенств начнём с курса математики начальных классов.

1. В нач.классах рассматриваются след. линейные ур-я: 7+x=10, x-3=10+5, x(17-10)=70, x/2+10=30 и т. д. Неизвестное число сначала находят подбором, затем - используя связи между результатом и компонентами арифметич. действий. Знакомство с ур-нием проводится неформально. Нер-тва решаются подбором, причём в большинстве случаев ограничиваются нахождением лишь части решений нер-ств.

2. В 5 кл. ур-ия решают также на основе зависимости действия, при этом часто предварительно проводится упрощение выраж-ий. Учащиеся знаком. с применен. распред-го закона сложен. (вычитан.) к упрощению буквенных выражений. В 5 классе встречаются лишь отдельные примеры неравенств.

3. В 6 классе при изучении положит. и отрицат. чисел рассматриваются новые примеры линейных ур-ний, встречаются нелинейные ур-ния. На основан. определения противопол. чисел решаются ур-ния –x=607; - a= - 30,04. На основании модуля числа реш. ур-ния 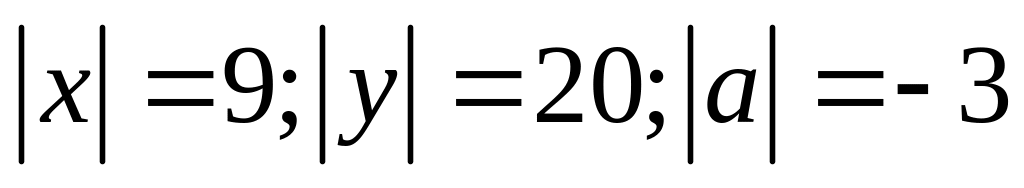. В 6 классе уч-ся знакомятся с тождест-м преобраз-ем «раскрытием скобок», также изучают условия рав-ва произведения нулю. Это помогает им решать ур-ния вида: 7,2 – (6,2 – x)=2,2; 4(x – 5)=0. Новым шагом в ознакомлении учащ-ся с методами решен. ур-ний явл. изучение правила переноса слагаемого из одной части ур-ния в другую. С помощью этого правила решаются такие ур-ния: 15y – 8= - 6y+4,6; 6x – 12=5x+4/

4. В 7 классе систематизируются сведения о решении лин-ых ур-ний. В некот. уч-х пособиях уточняется различ. между ур-нием первой степени (kx + b=0, k≠0) и лин-м ур-нием (kx + b=0, k), показыв-cя, что ур-ние первой степени явл. частным случаем лин. ур-ния. Существенным шагом в 7 кл. явл. введение понятия равносильных ур-ний. Индуктивным путём подтверждается справедливость след. теорем: «Если к обеим частям ур-ния прибав. одно и тоже число, то получ. ур-ние, равнос-е данному»; «если обе части ур-ния умнож. или раздел. на одно и тоже ≠ 0 число, то получ. ур-ние, равнос. данн-у».

Прогр-а для 11летн. ср.шк. сохран. тенденц. к раннему введен. лин. ур-й с 2я неизв. и их систем.

Одним из психологич. аспектов обучен. матем-е явл. мотивировка изучения нового уч.материала. Рассм. этот вопрос применительно к введению новых видов ур-ний. В методике мат-ке  понятие обратных задач. Поясним это понятие. Пусть, в одной задаче речь идёт о велич-х x, y и z, причём вел-ны x и y явл. данными, а z – искомой. Составим новую задачу, в кот., напр., велич-ы x и z явл. данными, а y – искомой. При этом фабулу задачи оставим без изменения. 2 такие задачи счит-ся взаимно обратными. Часто при решении таких задач используются различные типы ур-ний. Поэтому составление и решение обратных задач служит полезным методическим приёмом мотивации изучения новых видов уравнений.

Пример таких задач.

К ½ прибавили некоторое число. Получили число, обратное ½. Какое число прибавили?

К некоторому положит. числу прибавили 1,5. Получили число, обратное первому. Найти это число.

По мере расширения набора методов реш. ур-ний у уч-ся возн-ют затруднения в их выборе. В этой связи полезны спец. задан. на определ-е способа реш. ур-й. Выполнение таких заданий целесообр. про-водить в 2 этапа: 1)вначале для группы ур-ий указать только способ реш-я; 2)после этого решить ур-я.

Графич. метод реш-я урав-й и нер-тв тесно связывает ур-ия и нер-ва с функц-и. Иногда в таких случ. говорят о функциональном подходе к решению уравнений и неравенств. Существует некоторые приёмы сочетания графического и аналитического методов решения уравнений и неравенств.

Рассм. некот. приёмы применения функционального подхода при решении уравнений и неравенств.

• Иногда при решении ур-ния f(x)= 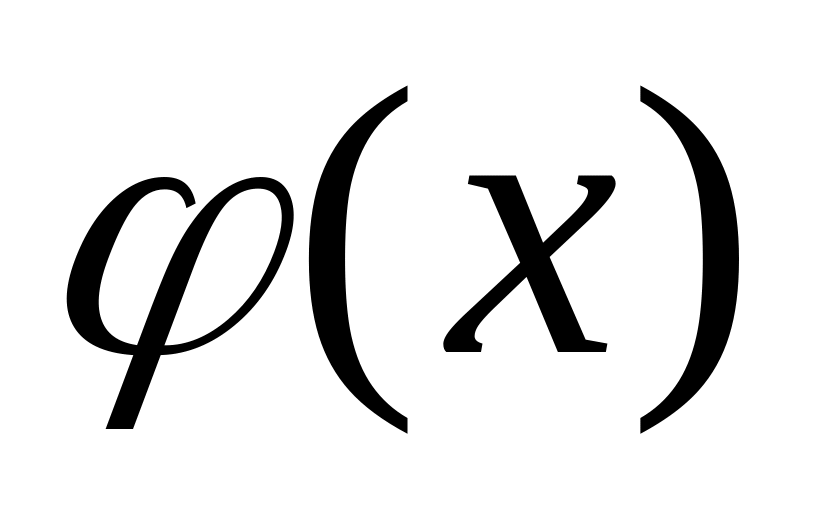полезно найти области определения фун-й f(x) и . Напр, пусть требуется решить уравнение 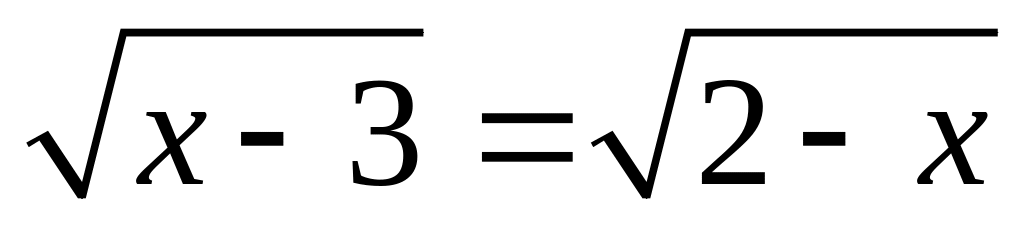. Имеем: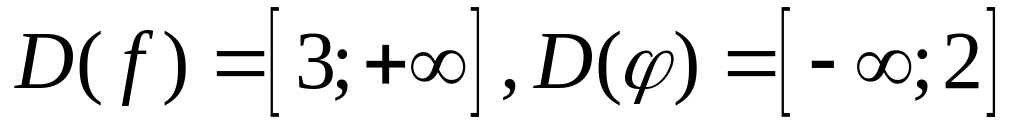 .Так как 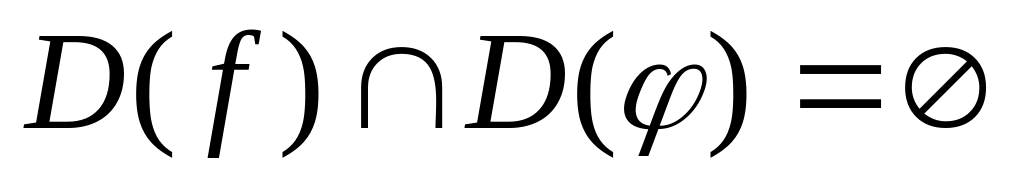, то данное уравнение корней не имеет.

• Функц-ый подход к реш. нер-тв лежит в основе метода интер-в. Решите методом интер-в след. нер-во:

(x+1)(x – 4)(x+8)>=0. Какие свойства функции f(x)= (x+1)(x – 4)(x+8) при этом используется?

• В некот-х случаях полезным оказывается использование понятия производной ф-ции. Пусть требуется доказать тождество arcsinx+arccosx=π/2. Рассм. ф-цию f(x)=arcsinx+arccosx. Найдём её производную:

f'(x)=(arcsinx)'+(arccosx)'=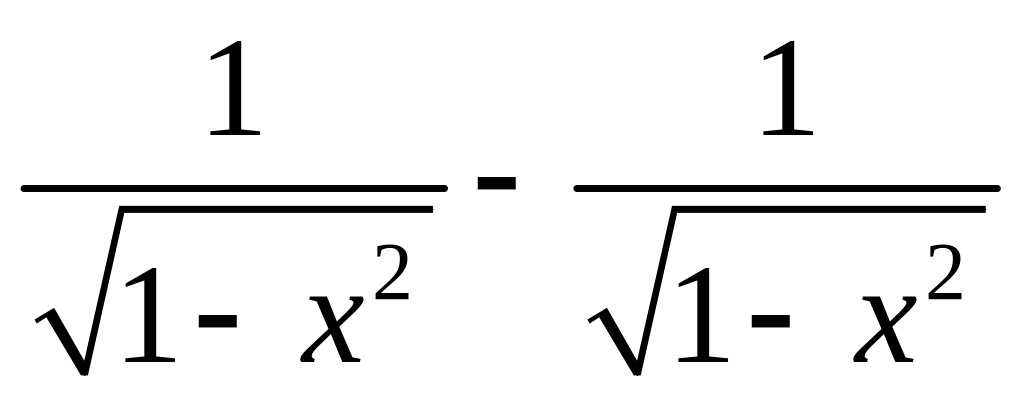 =0, так как f'(x)=0, то f(x)=с, где с – постоянная. Найдём с, вычислив для этого . Имеем с= = arcsin0+arccos0=0+π/2=π/2, отсюда arcsinx+arccosx=π/2.