32. Методика изучения общих свойств функций.

Просто необходимо знать основные свойства функций, т.к. они позволяют значительно упростить решение сложных уравнений, неравенств и др. Наиболее известные свойства функций формулируются без доказательств:

1. Сумма 2 возраст.(убывающих) функций есть возрастающая(убывающая) функция.

2. произведение 2 положительных возрастающих(убывающих) функций есть возрастающая(убывающая) функция.

3. Если функция определена и непрерывна на [a,b] и на концах этого промежутка она принимает значения разных знаков, то внутри этого промежутка существует такая точка x1, где f(x1)=0

4. Если функция определена, непрерывна и строго монотонна на [a,b] и на концах этого промежутка она принимает значения разных знаков, то внутри этого промежутка существует единственная точка x1, где f(x1)=0

5. Пусть функция определена и непрерывна на некотором промежутке. Если в двух точках из этого промежутка x=a, x=b(a<b) она принимает разные значения f(a)=A, f(b)=B, то внутри этого промежутка существует такая точка c(c из(a,b)), где f(c)=C (C из (A,B))

6. Если функция определена, монотонно возрастает(убывает) и непрерывна на [a,b], то на [f(a),f(b)] существует такая функция y= 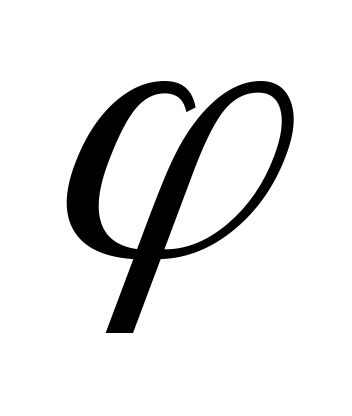(x), также монотонно возрастающая(убывающая) и непрерывная.

7. Пусть функция определена на некотором промежутке и во внутренней точке 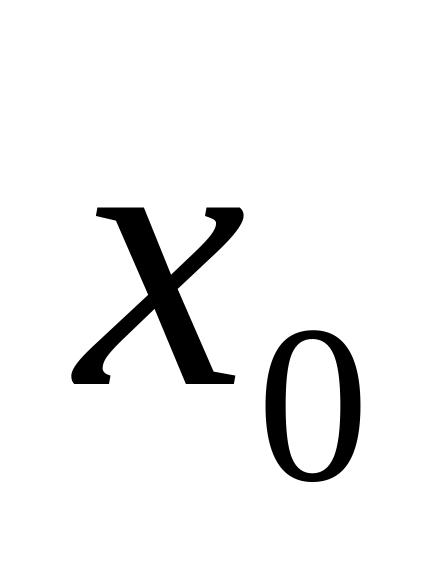этого промежутка принимает наибольшее(наименьшее) значение. Если существует двусторонняя конечная производная 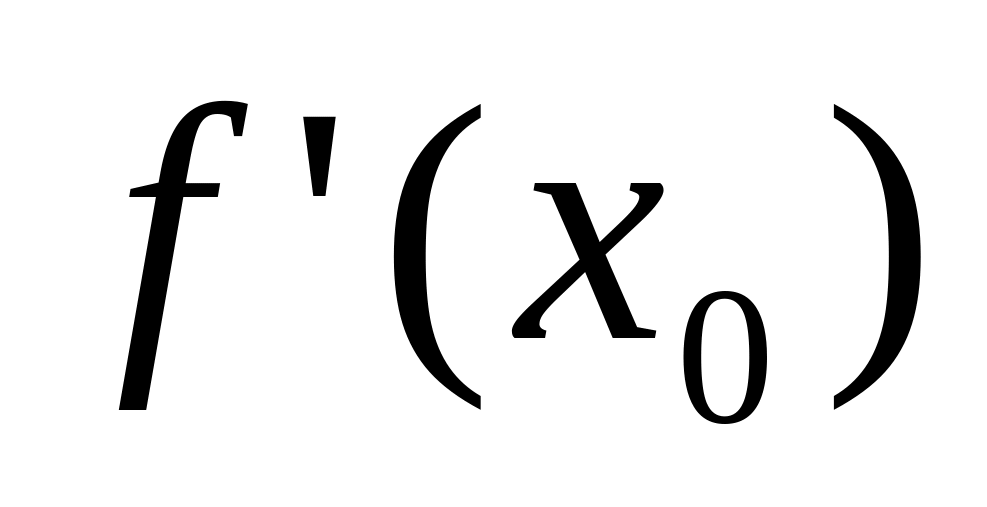, то необходимо =0

8. Произведение выпуклой(вогнутой) функции на положительную постоянную есть выпуклая(вогнутая) функция.

9. Произведение выпуклой(вогнутой) функции на отрицательную постоянную есть вогнутая (выпуклая) функция.

10. Сумма 2 выпуклых функций есть выпуклая функция.

Общая схема исследования свойств функции на четность и нечетность, на монотонность и экстремумы (с применением производной или без применения производной), нахождение нулей функции.

Функция называется периодической, если существует такое число L не равное 0( период f), что при любом значении x из ее области определения числа x-L и x+L принадлежат области определения функции f и f(x-L)=f=f(x+L)

34. Определение целых корней уравнений и их систем

Метод решения уравнения относительно одного из неизвестных

Данное уравнение с несколькими переменными Е (х, у, х, …u,v) = 0 решается относительно одного из этих переменных, например v. После этого исследуется функция v=f(х, у, z, ... , u).

Пример 1. Решить в целых числах уравнение xy = х + у.

Из данного уравнения получаем Теперь понятно, что х будет целым только в том случае, если 1/y-1. Но дробь 1/y-1 — целое число. если у-1=1 или у-1=-1.

Следовательно, y1=2, у2 = 0, и мы получим два ответа:

1. х1=2, у1=2; 2) х2 = 0, y2=0

Разложение на множители выражений, входящих в уравнение

Пример 2. Доказать, что уравнение не имеет решений в натуральных числах.

Преобразуем данное уравнение к виду

Это уравнение эквивалентно системе уравнений:

Но эта система противоречива. Утверждение задачи доказано.

Определение рациональных корней уравнения

Теорема: Если несократимая дробь является корнем многочлена

(1)

с целыми коэффициентами, то делится на р, а — на q.

Доказательство. Пусть = p/q — корень данного многочлена . Подставив в равенство (1) вместо х число р/q и приведя его к общему знаменателю, получим (2)

Отсюда

Так как числа и p взаимно простые, то делится на р.

Теперь преобразуем уравнение (2) к виду

Числа р и q взаимно простые, поэтому делится на q.

Теорема доказана.

Покажем, как применяется эта теорема к отысканию рациональных корней целых функций с целыми коэффициентами.

Пример 3. Определить рациональные корни уравнения

Здесь =1, =3. Поэтому рациональные корни данного уравнения следует искать среди чисел 1, -1, 3, -3. Подстановкой этих чисел в данное уравнение убеждаемся, что только числа 1 и З являются его корнями. Нужно только выяснить, не являются ли эти корни кратными. Для этого разделим левую часть уравнения на (х-1)(х-З). По теореме Безу это можно сделать. Получим

Отсюда

Уравнение не имеет целых корней, и корни являются однократными.