Глава 3. Процессы с идеальным газом

3 - 1. Основные свойства идеального газа

Как уже указывалось, идеальный газ является воображаемой системой, которой приписываются определенные свойства. Прежде всего зависимость между параметрами идеального газа устанавливается уравнением состояния (напомним, что оно относится к 1 моль газа или смеси различных газов)

PV=RT (3 - 1)

Еще одно свойство газов при низких давлениях, т.е. приближающихся по свойствам к идеальному газу, было установлено Гей-Люссаком и подтверждено Джоулем и другими исследователями. Оно заключается в следующем.

Если газ быстро (без теплообмена) выпускать в пустоту, то его температура не изменится. При вытекании газа увеличивается его объем и падает давление. В то же время при истечении газа в пустоту он не испытывает сопротивления среды и, следовательно, не совершает работу. Отсутствие работы и теплообмена означает, что внутренняя энергия газа не изменяется.

Таким образом, не вызывающее изменения внутренней энергии истечение газа в пустоту влияет на объем и давление, но не влияет на температуру.

Внутренняя энергия идеального газа зависит только от темпера­туры.

Это утверждение, известное как закон Гей-Люссака - Джоуля, является вторым важнейшим свойством идеального газа.

Особенности идеального газа связаны также с его теплоемкостями.

Установлено, что теплоемкость газа при постоянном объеме C_v не зависит от температуры, но зависит от числа атомов, составляющих молекулу газа. В частности, для одноатомных молекул, к числу которых можно отнести атомы инертных газов, для теплоемкости С_v выполняется условие

, (3 - 2)

для двухатомных молекул -

, (3 - 3)

для молекул, состоящих из трех и более атомов -

. (3 - 4)

Используя уравнение состояния для идеального газа, его энтальпию можно выразить следующим образом:

H = U + RT. (3 - 5)

Изменение энтальпии можно записать так:

dH = dU + RdT. (3 - 6)

Из равенств (2 - 11) и (2 - 15) следует

C_pdT = C_vdT + RdT

или

C_p = C_v + R (3 - 7)

Равенство (3 - 7) известно под названием формулы Майера, выведшего ее в начале 40-х годов XIX в.

3 - 2. Политропические процессы с идеальным газом

В этой главе рассматриваются только квазистатические процессы в простых системах.

Политропическими процессами называются процессы, в ходе которых зависимость между параметрами имеет вид

. (3 - 8)

Уравнение (3 - 8) называется уравнением политропы, а показатель степени n - показателем политропы.

Другие формы уравнения политропы можно получить, если воспользоваться уравнением состояния идеального газа. Подставляя в уравнение (3 - 8) вместо давления RT/V, получим

, (3 - 9)

а подставляя V вместо RT/P, получим

. (3 - 10)

Для вывода уравнения политропы используем уравнение баланса энергии и свойства идеального газа:

Q = dU + PdV ;

Q = CdT; dU = C_vdT; dT = R^-1(PdV + VdP); C_p - C_v = R.

Далее можно записать:

CdT = CvdT + PdV;

(C - C_v)dT = PdV;

(C - C_v)R^-1(PdV + VdP) = PdV;

(C - C_v)( PdV + VdP) = RPdV = (Cp - Cv)PdV;

(C - C_v)VdP + (C - C_p)PdV = 0.

Разделив обе части последнего равенства на PV и на (C - C_p), получим:

.

Интегрирование приводит к следующему выражению:

.

Окончательная форма уравнения имеет следующий вид:

. (3 - 11)

Сравнивая две формы записи уравнения политропы (3 - 8) и (3 - 11), находим, что показатель политропы определяется теплоемкостью процесса

. (3 - 12)

Рассмотрим, какие значения принимает показатель политропы для важнейших термодинамических процессов.

Изотермический процесс. Ранее было показано, что при приближении процесса к изотермическому его теплоемкость стремится к двум значениям: +  или - . Следовательно, показатель политропы стремится к 1.

Таким образом, уравнение изотермы

PV=const

является частным случаем политропы.

Изобарический процесс. Приближение процесса к изобарическому означает, что для его теплоемкости выполняется условие C  C_p. Следовательно, n  0. В этом случае уравнение (3 - 9) примет вид

V^-1T=const

или

,

что соответствует закону Гей-Люссака.

Изохорический процесс. Из условия C  C_v следует, что n   и . Переписав уравнение (3 - 10) в форме

,

получим

.

Последнее уравнение соответствует закону Шарля.

Адиабатический процесс. Для этого процесса выполняется условие C=0. Показатель степени становится равным

. (3 - 13)

Вводимый равенством (3 - 13) показатель  называется показателем адиабаты.

Уравнение адиабаты, связывающее параметры идеального газа в адиабатическом процессе, имеет следующие формы:

, (3 - 14)

, (3 - 15)

. (3 - 16)

Уравнение адиабаты можно вывести, принимая, что теплота процесса Q=CdT=0 и изменение внутренней энергии равно dU=C_vdT. Исходное уравнение таково:

C_vdT + PdV = 0.

Для его решения используются те же приемы, что и для вывода уравнения (3 - 11).

3 - 3. Циклические процессы с идеальным газом. Термодинамический КПД

Рис. 3 - 1. Прямой цикл, состоящий из двух изобар и двух изохор.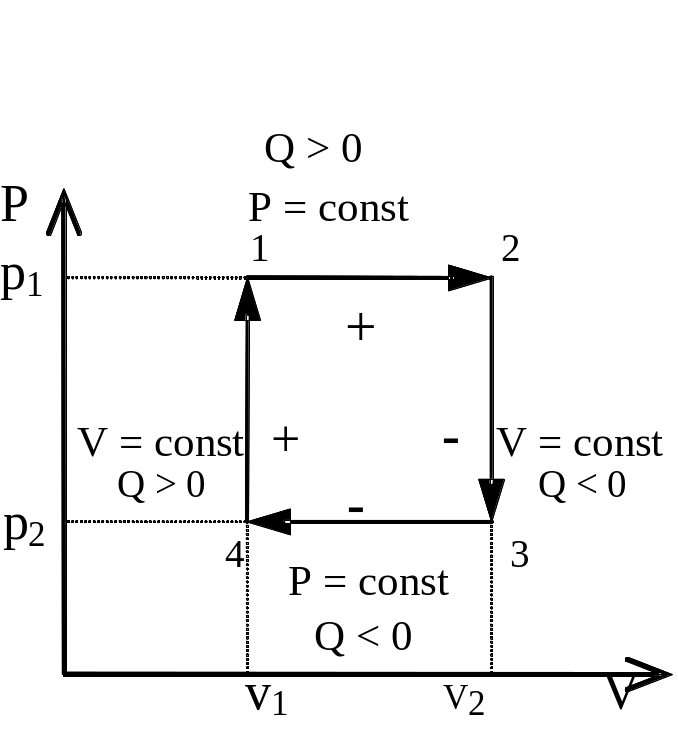

В качестве примера циклического процесса с идеальным газом рассмотрим процесс, состоящий из двух изобар и двух изохор (рис. 3 ‑ 1).

Пусть процесс начинается из точки 1, которой соответствуют давление Р₁ и объем V₁. Газ изобарически расширяется до объема V₂ в точке 2. Этому процессу соответствует площадь между изобарой и осью объемов. Далее давление газа изохорически падает от P₁ в точке 2 до P₂ в точке 3. Затем газ при давлении P₂ изобарически сжимается от объема V₂ в точке 3 до объема V₁ в точке 4. Совершаемая при этом работа над газом равна площади между нижней изобарой и осью объемов со знаком минус. Последней стадией цикла является изохорическое повышение давления от P₂ в точке 4 до Р₁ в точке 1.

Полная работа цикла равна площади фигуры, ограниченной его контуром. Так как работа, совершаемая по верхней изобаре, по абсолютной величине превосходит работу по нижней изобаре, то площадь фигуры имеет положительную величину.

Вообразим, что цикл совершается в противоположном направлении:

изохорическое уменьшение давления от точки 1 до точки 4, изобарическое расширение от точки 4 до точки 3, изохорическое повышение давления от точки 3 до точки 2, изобарическое сжатие от точки 2 до точки 1. В новом цикле расширение по нижней изобаре сопровождается положительной работой, а сжатие по верхней изобаре - отрицательной. Полная работа нового цикла оказывается отрицательной величиной.

Из изложенного следует вывод, что работа цикла зависит от направления обхода по контуру. В первом случае обход совершался по часовой стрелке, во втором - против часовой стрелки.

Таким образом, для цикла, совершаемого с обходом по контуру по часовой стрелке, работа положительна, а для цикла с обходом по контуру против часовой стрелки работа отрицательна.

Цикл с суммарной положительной работой называется циклом двигателя, рабочим циклом или прямым циклом.

Цикл с суммарной отрицательной работой осуществляется при условии, что отбираемая из системы при более низкой температуре теплота поступает во внешнюю среду при более высокой температуре. Такой цикл называется холодильным или обратным циклом.

Термодинамическим коэффициентом полезного действия (КПД) цикла называется отношение работы к подводимой теплоте для прямого цикла или отношение работы цикла к отводимой теплоте для обратного цикла.

Для рассматриваемого цикла, состоящего из двух изобар и двух изохор, работа цикла равна площади внутри его контура: W=(P₂-P₁)(V₂-V₁). Эта же работа в соответствии с первым началом термодинамики равна сумме всех теплот цикла, т.е.

W=Q_1-2+Q_2-3+Q_3-4+Q_4-1.

В прямом цикле теплота подводится при изобарическом расширении из точки 1 в точку 3 (Q_1-20) и при изохорическом повышении давления при переходе из точки 4 в точку 1 (Q_4-10). Поэтому термодинамический коэффициент  данного цикла равен

.

Теплоты процессов 1 - 2 и 4 - 1 можно найти, используя данные по теплоемкости C_V и уравнение состояния идеального газа. Температуры в точках 1, 2 и 4 соответственно равны

.

Затем записываем выражения для расчета теплот

Q_1-2=(C_v+R)(T₂-T₁); Q_4-1=C_v(T₁-T₄) и т.д.

Термодинамический КПД всегда меньше 1.

3 - 4. Цикл Карно с идеальным газом

Цикл Карно состоит из двух изотерм и двух адиабат.

Рис. 3 - 2. Прямой цикл Карно.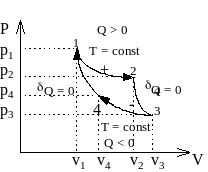

Проведение прямого цикла Карно представим следующим образом (рис. 3 - 2).

Идеальный газ при постоянной температуре расширяется от точки 1 до точки 2. Затем адиабатически расширяется от точки 2 до точки 3. Из точки 3 изотермически газ сжимается до точки 4. Последней частью цикла является адиабатическое сжатие от точки 4 до точки 1.

Термодинамический КПД цикла находим как отношение суммы всех теплот к подводимой теплоте.

Теплообмен осуществляется при изменении объема по обеим изотермам.

Теплота изотермического процесса в соответствии с законом Гей-Люссака - Джоуля равна его работе. В частности,

,(3 - 17)

.

Термодинамический КПД цикла Карно можно выразить следующим отношением:

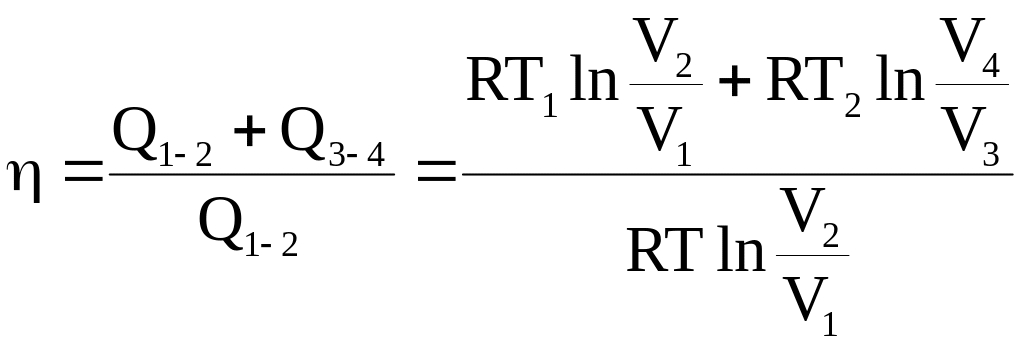. (3 - 18)

Выражение (3 - 18) можно существенно упростить, используя следующие условия:

точки 1 и 2 лежат на одной изотерме, т.е.

P₁V₁=P₂V₂ ; (a)

точки 3 и 4 также принадлежат одной изотерме

P₃V₃=P₄V₄ ; (b)

точки 2 и 3 лежат на одной адиабате

; (c)

точки 4 и 1 также лежат на одной адиабате

. (d)

Комбинируя равенства (a) и (b) и равенства ( c) и (d), получим

(e)

и

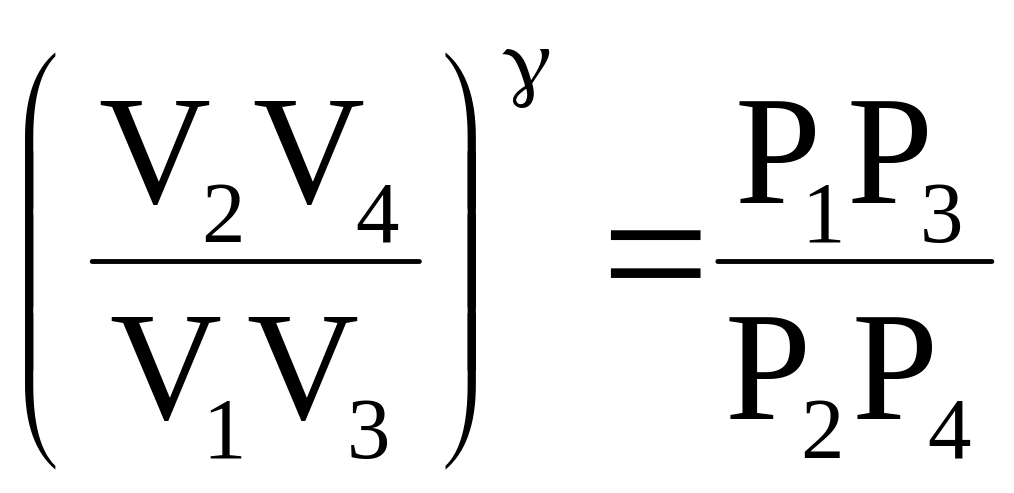. (f)

Из равенств (e) и (f) следует

и .

Окончательно имеем для КПД цикла Карно с идеальным газом

(3 - 19)

Из уравнения (3 - 19) следует, что КПД цикла Карно с идеальным газом определяется только его температурными пределами.

Независимость КПД цикла Карно с идеальным газом от расстояния между адиабатами позволяет доказать замечательную предварительную теорему, которая впоследствии будет обобщена на реальные системы (газы, пары и другие).

С именем Карно связано создание всего раздела науки и ее название - «термодинамика». Никола Леонар Сади Карно, родившийся в 1796 г., был сыном знаменитого французского ученого, инженера, общественного деятеля и военачальника, генерала французской армии Лазара Карно. Увлекаясь искусством, Лазар Карно назвал своего старшего сына именем великого персидского поэта и мудреца, автора всемирно известных поэм «Бустан» и «Гулистан» Саади. В 16 лет С.Карно поступил в одно из лучших высших учебных заведений начала XIX в. Политехническую школу в Париже. Преподавателями в ней работали Ампер, Бертоле, Лагранж, Лаплас, Фурье и др., а среди студентов были Гей-Люссак, Клапейрон, Коши, Пуазейль, Пуассон, Френель. В 18 лет Сади Карно поступает на военную службу. Его единственная работа «О движущей силе огня и машинах, способных развивать эту силу» была опубликована в 1824 г. К этому времени он уже был известным специалистом в области торговли и организации промышленности. Однако его книга оказалась практически незамеченной. Чтобы целиком посвятить себя научной работе, Сади в 1828 г. оставляет службу. В возрасте 36 лет, заболев холерой, он умирает. В результате последовавшей дезинфекции помещения, где он жил, практически все оставшиеся после него рукописи были уничтожены. Имя Сади Карно, в отличие от его отца и младшего брата Ипполита, занимавшегося политической деятельностью, было почти полностью забыто. Однако Бенуа Поль Эмиль Клапейрон уже в 1834 г., основываясь на работе С.Карно, находит зависимость между давлением, температурой, теплотой и изменением объема при изменениях агрегатного состояния веществ. Благодаря работам Клапейрона, получившим широкую известность, идеи С.Карно стали распространяться. С ними познакомился У.Томсон, увидевший, что они являются основой новой науки, и предложивший для нее название, дублирующее название работы С.Карно, - термодинамика (греч. dynamis - сила, греч. thйrmé - тепло, жар).

3 - 5. Предварительная теорема Карно

Формулировка предварительной теоремы Карно:

Из всех циклических процессов, совершаемых квазистатически в данном температурном интервале, максимальным термодинамическим КПД обладает цикл Карно.

Рис. 3 - 3. Произвольный цикл и описанный вокруг него цикл Карно в тех же температурных пределах.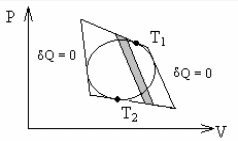

Для доказательства возьмем произвольный цикл, как это показано на рис. 3 - 3.

Рис. 3 - 4. Сравнение фрагментов произвольного цикла и внутреннего цикла Карно.

Чтобы найти температурные пределы этого цикла, проведем изотермы. Верхняя изотерма, касающаяся цикла, соответствует его максимальной температуре (обозначим ее Т₁), а нижняя изотерма, также касающаяся цикла, - нижней минимальной температуре (примем ее равной Т₂). Далее проведем две адиабаты, касающиеся произвольного цикла. Заключенный между касательными изотермами и касательными адиабатами цикл является циклом Карно, проводимым в тех же температурных пределах, что и произвольный цикл.

Проведя произвольно на очень малом расстоянии друг от друга две адиабаты, выделим фрагменты произвольного цикла и цикла Карно (рис. 3 - 4). КПД фрагмента цикла Карно, описанного вокруг произвольного цикла, совпадает с КПД всего внешнего цикла Карно.

Площадь, ограниченная верхним и нижним фрагментами произвольного цикла и двумя боковыми адиабатами, равна сумме теплот Q_ и Q_. Теплота Q_ соответствует верхнему участку, а Q_ - нижнему. Сохраняя площадь выделенной части неизменной, проведем вместо верхнего фрагмента произвольного цикла изотерму. Обозначим ее температуру T₁`. Теплота процесса остается прежней: Q+Q. Так как теплота нижней части фрагмента Q осталась неизменной, то теплота процесса по изотерме, заменяющей верхнюю часть фрагмента произвольного цикла, окажется равной Q. Далее, заменяя нижнюю часть фрагмента соответствующей изотермой с температурой Т<sub>2</sub>`, получим внутренний цикл Карно.

Термодинамический КПД цикла Карно, описанного вокруг произвольного цикла, обозначим _e, а КПД цикла Карно, заменяющего фрагмент произвольного цикла, - _i.

Поскольку изотерма с температурой Т₁ лежит выше изотермы с температурой Т₁`, а изотерма с температурой Т<sub>2</sub> находится ниже изотермы с температурой Т<sub>2</sub>`, то выполняются следующие неравенства:

T₁>T₁` , T<sub>2</sub> <T<sub>2</sub>` ;

; ; ;

.

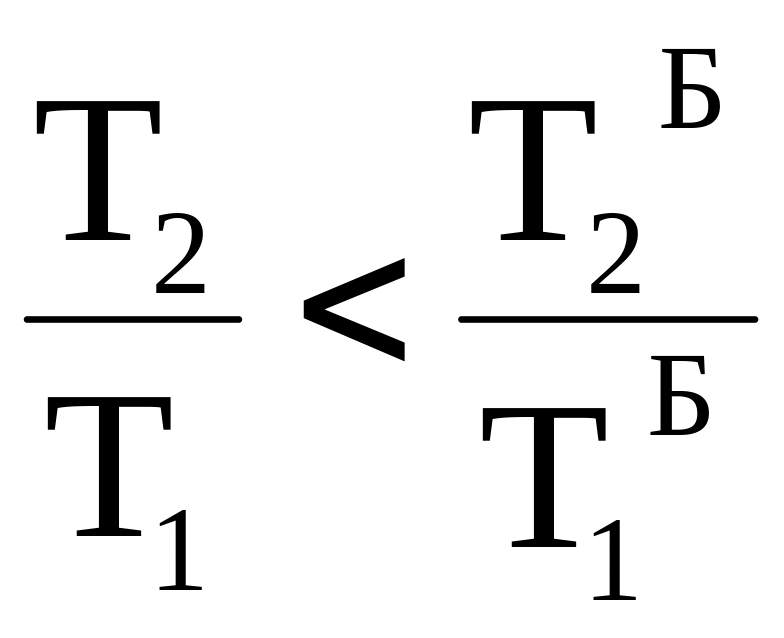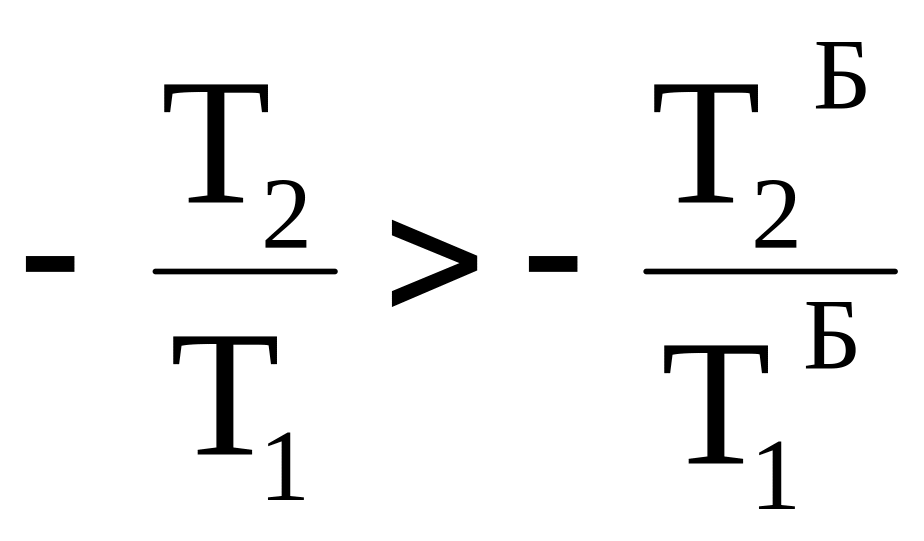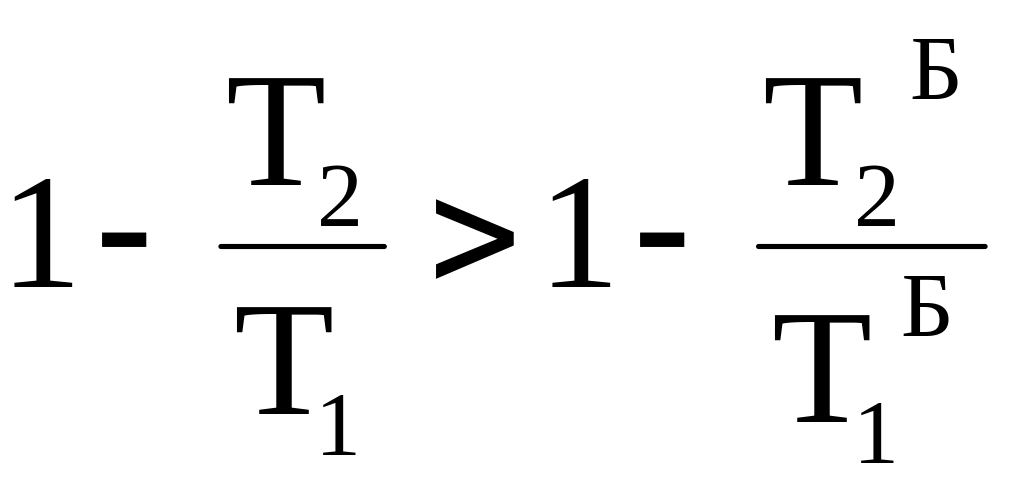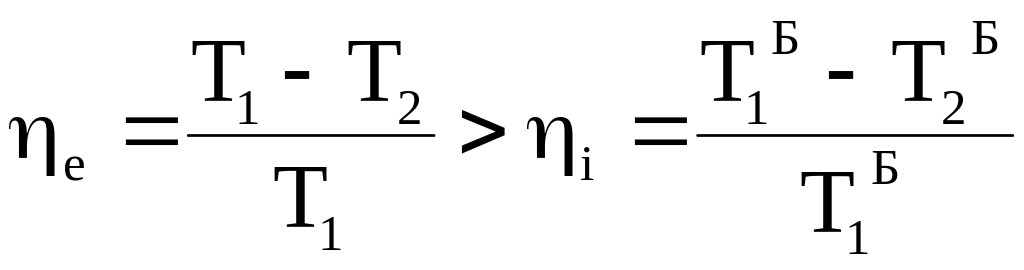Таким образом, термодинамический КПД любого фрагмента произвольного цикла всегда меньше КПД цикла Карно, проводимого при максимальной и минимальной температуре произвольного цикла. КПД всего произвольного цикла также должен быть меньше КПД цикла Карно, проводимого в том же температурном интервале.

3 - 6. Приведенные теплоты цикла Карно с идеальным газом. Температура как интегрирующий делитель в квазистатических процессах с идеальным газом

Приведенной теплотой называется отношение теплоты политропического процесса к температуре, при которой он проводится.

Строго этому определению удовлетворяет изотермический процесс. Однако если теплота других процессов является величиной очень малой, то можно рассматривать элементарную приведенную теплоту в виде Q/T.

Как уже было показано, для квазистатического цикла Карно выполняется равенство

,

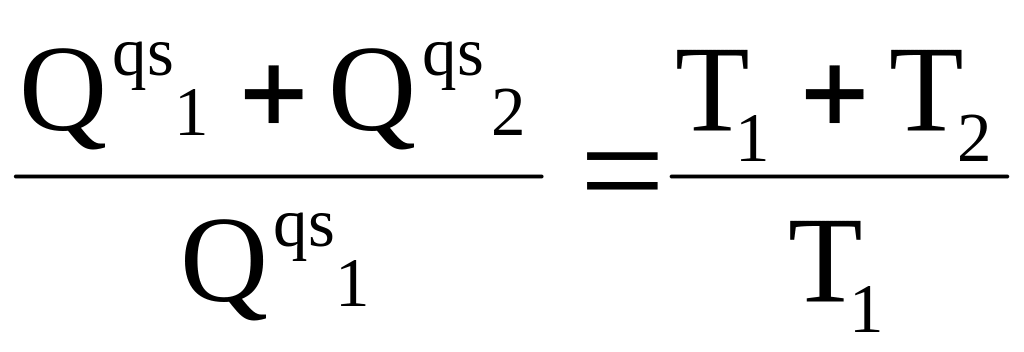в котором символ qs обозначает, что речь идет о теплоте квазистатического процесса.

Проведя несложные преобразования, получим

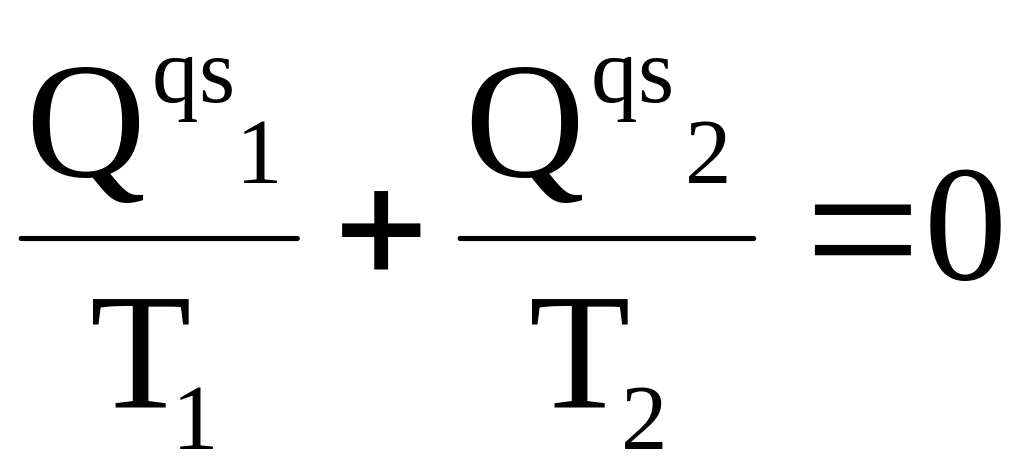. (3 - 20)

Равенство (3 - 20) означает, что

в проводимом квазистатическом цикле Карно сумма приведенных теплот всегда равна нулю.

Этот результат распространяется и на бесконечно малые циклы Карно, к которым относятся циклы с бесконечно малым расстоянием между изотермами (в этих циклах теплоты изотерм являются конечными величинами) или бесконечно малыми расстояниями между адиабатами (теплоты бесконечно малых изотерм также являются бесконечно малыми).

Для циклов Карно с бесконечно малым расстоянием между адиабатами выражение (3 - 20) можно записать в форме

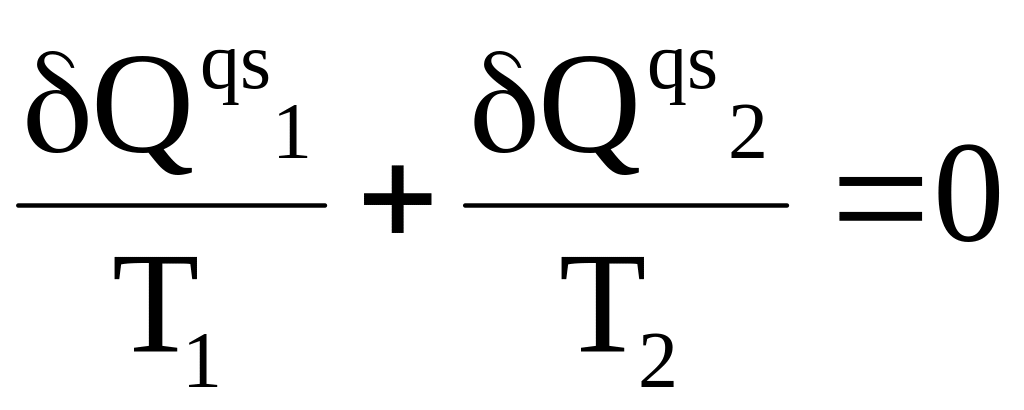(3 - 21)

Выше было показано, что совершаемый квазистатически произвольный цикл можно заменить бесконечно малыми изотермами, расположенными между соответствующими парами адиабат. Обход по всему произвольному циклу (по часовой стрелке) соответствует обходу справа налево по верхним изотермам (им соответствуют теплоты Q^qs ₁ ) и слева направо по нижним изотермам (соответствуют теплоты Q^qs ₂ ) . Поэтому, выбрав две точки 1 и 2 на контуре произвольного цикла (см. рис. 3- 3), можем записать

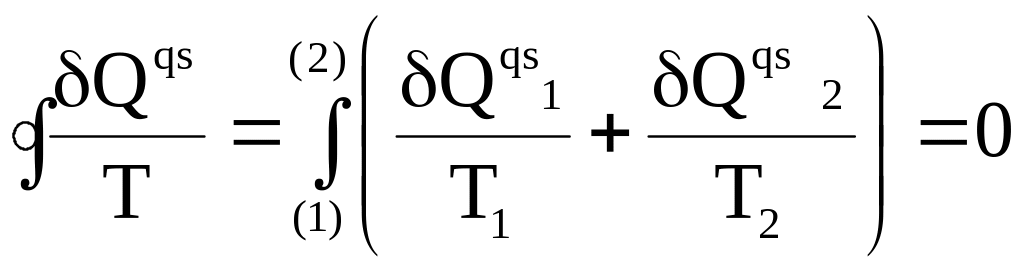(3 - 22)

Из равенства (3 - 22) следует, что величина Q^qs /T представляет собой приращение некоторой функции, так как только в этом случае ее интеграл по замкнутому контуру равен нулю.

Получен замечательный результат:

в квазистатическом процессе с идеальным газом приведенная элементарная теплота совпадает с приращением некоторой функции.

Это означает, что по крайней мере для идеального газа изменение этой функции при переходе из одного и того же исходного состояния в одно и то же конечное состояние не зависит от процесса.

Существует также аналитический способ получения подобного результата для идеального газа.

Записав для идеального газа баланс энергии в форме

и разделив части равенства на Т, получим

.

Вследствие равенства частных производных

приведенная теплота является приращением функции состояния.

Таким образом, делением на температуру теплота, являющаяся характеристикой процесса, становится величиной, приращение которой от процесса не зависит. Температура приобретает свойство интегрирующего делителя для теплоты квазистатического процесса.

Свойство температуры как интегрирующего делителя нами установлено только для идеального газа. Возможность обобщения результата на любые системы выходит за пределы первого постулата термодинамики.