Глава 11. Элементы статистической термодинамики

11 - 1. Термодинамическая вероятность

Вообразим следующий эксперимент, реальное проведение которого невозможно.

В системе (возможно, ею окажется идеальный газ) каким-то образом пометим и сфотографируем все молекулы с таким расчетом, чтобы можно было определить их энергию. Результаты такого эксперимента представим в виде таблицы, в которой приводятся все возможные значения энергии молекул в системе и число молекул с каждым значением энергии.

Таблица 11 - 1.

Условное распределение молекул по энергиям

Значения энергии	1	2	3			i		
Число молекул с данным значением энергии	N1	N2	N3			Ni		

Если молекулы помечены, т.е. различимы, то появляется возможность подсчитать число способов распределения молекул по значениям энергии наподобие того, как рассчитывается размещение жильцов по домам (см. приложение). Для этого воспользуемся формулой

. (11 - 1)

Число способов распределения молекул по энергиям W называется также числом способов реализации данной системы или (что наиболее распространено) термодинамической вероятностью .

Отметим, что термодинамическую вероятность с математической вероятностью объединяет название и единственное свойство, с которым познакомимся при дальнейшем рассмотрении этого понятия. Различия между ними весьма существенны. Минимальное значение математической вероятности равно 0 (невозможное событие), а максимальное равно 1 (абсолютно достоверное событие). Минимальное значение термодинамической вероятности составляет 1 (молекулы могут быть распределены по энергиям единственным способом). Верхнего предела для термодинамической вероятности нет.

Если бы значения чисел были невелики, то для расчетов термодинамической вероятности можно было воспользоваться уравнением (11 - 1) в исходной форме. Для больших чисел, а именно с ними приходится сталкиваться, оперируя с числом молекул в системе, применяется замечательное приближение

, (11 - 2)

называемое формулой Стирлинга .

Можно воспользоваться более грубым, но достаточным для наших целей приближением, учитывающим, что для больших чисел n>>2 и ln n<<n,

. (11 - 3)

Расчетная формула для термодинамической вероятности системы с реальным числом частиц принимает следующий вид:

.

Так как N_i=N, то формула становится еще проще:

. (11 - 4)

Найдем термодинамическую вероятность системы, образованной сложением равновесных подсистем, одна из которых содержит aN частиц, а другая содержит bN частиц. Относительное распределение частиц по энергиям в равновесных системах совпадает. Поэтому расчет термодинамической вероятности по составной формуле (11 - 4) приводит к следующему:

Принимая во внимание, что число подсистем значительно меньше числа частиц в каждой из них, т.е. a+ b<<N_i, получим

или

, (11 - 5)

так как .

Формула (11 - 5) показывает, что термодинамическая вероятность системы, полученной сложением подсистем, равна произведению термодинамических вероятностей подсистем. Это свойство термодинамической вероятности называется мультипликативностью .

Мультипликативность характерна и для математической вероятности. Как известно, математическая вероятность исхода нескольких независимых событий равна произведению вероятностей исхода каждого из них.

11 - 2. Зависимость между термодинамической вероятностью и энтропией. Формула Больцмана

Одним из свойств энтропии является аддитивность. При сложении двух равновесных систем a и b, энтропии которых соответственно равны S_a и S_b, энтропия вновь образованной системы находится из условия

. (11 - 6)

Если энтропия является функцией термодинамической вероятности, то эта функция должна обладать свойством, вытекающим из мульти­пликативности термодинамической вероятности:

.

Свойством аддитивности при мультипликативности аргумента обладает логарифмическая функция

(11 - 7)

Формула (11 - 7), устанавливающая зависимость между энтропией и термодинамической вероятностью, была предложена Л.Больцманом и называется формулой Больцмана .

11 - 3. Распределение Больцмана

Обратимся к системе с дискретным спектром значений энергии молекул: ₁,₂,₃, ...,_i , ...

Если этими значениями энергии обладают молекулы, числа которых соответственно равны N₁, N₂, N₃, ..., Ni,..., то общее число частиц в системе равно

, (11 - 8)

а полная энергия системы равна

. (11 - 9)

Энтропию системы найдем по формуле Больцмана

. (11 - 10)

Для изолированной системы условием равновесия является максимум энтропии. Поэтому для нахождения распределения числа частиц по энергиям необходимо найти условие этого максимума. Простое дифференцирование функции S по числу частиц в данном случае непригодно, так как кроме основного уравнения (11 - 10) имеются дополнительные уравнения с теми же независимыми величинами - уравнения связи - (11 - 8) и (11 - 9). В этих условиях для нахождения экстремума используется метод неопределенных множителей Лагранжа. В соответствии с этим методом составляется функция

или

,.

где ₁ и ₂ - неопределенные множители Лагранжа.

Дифференцирование функции Ф с учетом

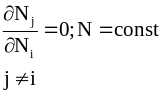
позволяет найти условие максимума энтропии:

. (11 - 11)

Преобразуем уравнение (11 - 11)

и введем новые обозначения для входящих в него констант:

.

Их применение упрощает форму записи уравнения (11 - 11)

. (11 - 12)

Потенцирование уравнения (11 - 12) дает

или, обозначив , получим

. (11 - 13)

От константы  можно избавиться следующим образом.

Суммируя N_i, получим

. (11 - 14)

Деление (11-13) на (11-14) дает

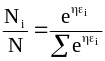. (11 - 15)

Уравнение (11 - 15) связывает число молекул (или других частиц) со значениями их энергии в системе. Таким образом, поставленная задача могла бы считаться решенной, если бы был ясен смысл входящей в уравнение (11-15) величины . Чтобы установить его, прологарифмируем уравнение (11 - 15)

,

умножим обе части уравнения на N_i

и просуммируем

или

. (11 - 16)

Обращаясь к уравнению (11 - 10), можно заметить, что левая часть равенства (11 - 16) равна . Следовательно,

. (11 - 16а)

При заданном энергетическом спектре системы, т.е. наборе значений энергии, и заданном числе частиц в системе последний член правой части равенства (11 - 16) является константой.

Исходя из изложенного, найдем приращения левой и правой частей равенства (11 - 16)

.

Из второго постулата термодинамики для системы, находящейся при постоянном объеме и не совершающей полезную работу, следует

.

Сравнение двух последних уравнений дает

. (11 - 17)

С учетом соотношения (11 - 17) уравнение, описывающее распределение частиц по энергиям, принимает следующий вид:

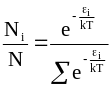(11 - 18)

Уравнение (11 - 18) называется уравнением Больцмана .

Входящая в уравнение (11 - 18) константа k называется константой Больцмана. Экспонента , определяющая относительное число частиц с данной энергией, называется фактором Больцмана . Сумма экспонент, входящая в знаменатель правой части уравнения (11 - 18), называется суммой по состояниям . Очень часто она обозначается f.

11 - 4. Константа Больцмана. Методы ее определения. Среднее значение энергии частиц

Установить зависимость между константой Больцмана и другими фундаментальными постоянными можно, приравняв величину средней энергии молекул, найденную разными способами.

С этой целью рассмотрим одноатомный идеальный газ, заключенный в кубическую емкость с длиной ребра а.

Пусть молярная масса вещества равна М, а средняя скорость движения молекул газа при температуре Т равна .

Энергия молекул определяется только кинетической составляющей, равной

,

где N_A - постоянная Авогадро (отношение молярной массы к постоянной Авогадро представляет собой массу одной молекулы).

Найдем импульс, получаемый стенкой при нормальном ударе одной молекулы:

.

Для того, чтобы определить число ударов молекул в единицу времени, необходимо учитывать, что движение молекул по каждому координатному направлению равновероятно. Поэтому принимается, что 1/3 молекул движется от одной стенки куба к противоположной и обратно.

Количество вещества n, содержащегося в кубической емкости с объемом а³, найдем по уравнению состояния идеального газа

,

а число молекул составляет

.

Как уже указывалось, 1/3 из этого числа движется в заданном направлении, причем каждая молекула совершает в единицу времени число пробегов от стенки и обратно, которое определяется равенством

.

Следовательно, число ударов всех молекул в единицу времени равно

,

а сила ударов по стенке составляет

.

Давление газа равно

.

Отсюда и средняя энергия одноатомной молекулы составляет

. (11 - 19)

Теперь найдем среднюю энергию молекулы, используя распределение Больцмана. Для этого несколько преобразуем формулу Больцмана.

Вновь обратимся к постулату о равноценности движения по всем направлениям и будем исходить из следующего условия.

Пусть для некоторой части молекул одноатомного газа импульсы находятся в пределах от P_x до P_x+dP_x, от P_y до P_y+dP_y и от P_z до P_z+dP_z.

Согласно распределению Больцмана доля этих молекул в общем числе молекул прямо пропорциональна фактору Больцмана . Кроме того, она должна быть прямо пропорциональна выделенному объему поля импульсов dP_xdP_ydP_z. Принимая, что число молекул dN с энергией  и заданным объемом поля импульсов dP_xdP_ydP_z является очень малой величиной, распределению Больцмана можно придать следующий вид:

. (11 - 20)

В уравнении (11 - 20)  - коэффициент пропорциональности. Для его определения воспользуемся тем, что общее число молекул в системе является постоянной величиной: N=const. Интегрирование уравнения (11 - 20) дает

.

Следовательно,

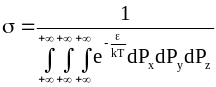
и распределение молекул одноатомного газа принимает вид:

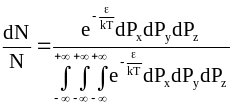. (11 - 21)

Уравнение (11 - 21) можно дальше преобразовывать, переходя к полярным координатам.

Элемент объема шарового слоя в полярных координатах равен

.

Зависимость между энергией и импульсами можно представить следующим образом:

или

,

из чего следует для частиц постоянной массы m

.

Заменим элемент объема поля импульсов на величину, определяемую только энергией молекул:

Переход от поля импульсов к распределению по энергии приводит к изменению пределов интегрирования. Скорость молекул может быть положительной и отрицательной, и пределы интегрирования по импульсам могут быть от + до -. Энергия может иметь минимальное значение, равное 0 и максимальное - условно равное .

С учетом изложенного получаем

.

Интеграл в приведенном выше уравнении является табличным интегралом следующего типа:

,

где Кроме того, .

Таким образом, уравнение Больцмана для распределения молекул по энергиям в непрерывном спектре можно записать в следующем виде:

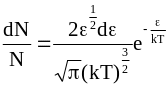. (11 - 22)

Среднее значение какой-либо величины при непрерывном распределении частиц представляет собой деленный на общее число частиц интеграл произведения этой величины на число молекул, обладающих ее значением Х:

.

Среднее значение энергии молекул одноатомного газа определяется по уравнению

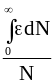(11 - 23)

или с учетом уравнения (11 - 22)

.

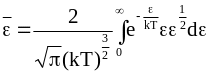Обращаясь вновь к табличному интегралу, найдем

. (11 - 24)

Сравнивая (11 - 19) и (11 - 24), имеем

. (11 - 25)

Молекулы одноатомного идеального газа участвуют только в поступательном движении по трем координатным направлениям. Число направлений движения называется также числом степеней свободы .

В предположении равноценности движения по каждому направлению уравнения (11 - 19) и (11 - 24) позволяют сделать важный вывод:

В идеальном газе на каждую степень свободы приходится энергия, равная 1/2kT.

Многоатомные молекулы кроме поступательного участвуют во вращательном движении. В частности, для двухатомных молекул существуют еще две степени вращательного движения.

Следовательно, энергия молекул двухатомного идеального газа равна 5/2kT.

Внутренняя энергия идеального газа определяется только кинетической составляющей молекул. Для одного моля частиц

.

В связи с этим производные внутренней энергии по температуре при постоянном объеме таковы:

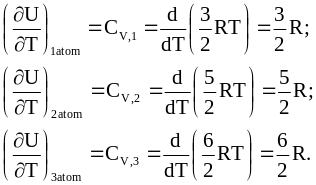(11 - 26)

Уравнения (11 - 26) объясняют природу теплоемкости идеального газа.

11 - 5. Примеры использования распределения Больцмана

Распределение частиц по высоте

Энергия частицы, находящейся на высоте h от отсчетного уровня в поле силы тяжести и имеющей массу m, плотность _p, равна

, (11 - 27)

а на отсчетном уровне она равна _о. В уравнение (11 - 27) входит также плотность среды _m.

Пусть N_h обозначает число частиц на высоте h, а N_o - на отсчетном (нулевом) уровне.

Число частиц на каждом уровне можно определить по уравнению Больцмана (11 - 18). Разделив N_h на N_o, можно избавиться от суммы по состояниям

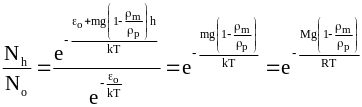^. (11 - 28)

Последняя часть уравнения (11 - 28) представлена в форме, содержащей молярную массу M=mN_A и универсальную газовую постоянную R=kN_A.

Совпадение уравнения (11 - 28) с уравнением (10 - 9), следующим из уравнений классической термодинамики, очевидно.

Уравнение (11 - 28) было использовано Перреном для экспериментального определения константы Больцмана и постоянной Авогадро.

Распределение заряженных частиц в электрическом поле

Энергия иона в электрическом поле равна

,

где _о - составляющая энергии, не зависящая от электрического поля,

i - знак заряда иона («+» для катиона и «-» для аниона),

z - заряд иона в атомных единицах заряда,

- электрический потенциал в данной точке раствора.

Приняв , что электрический потенциал в точке, значительно отдаленной от заряженной поверхности, равен нулю, можно найти отношение числа частиц в этих точках. Так как это отношение прямо пропорционально отношению концентраций, то получаемое уравнение совпадет с уравнением (10 - 11).

11 - 6. Связь между суммой по состояниям и термодинамическими функциями

Напомним, что сумма по состояниям представляет собой сумму всех возможных значений фактора Больцмана для данной системы

. (11 - 29)

Дифференцирование уравнения (11 - 29) по температуре при постоянном объеме дает

Разделив обе части равенства на f и умножив на kT², получим

..

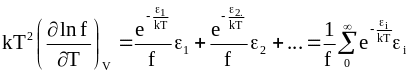Умножение на N приводит к следующему равенству:

,

правая часть которого представляет внутреннюю энергию системы.

Следовательно,

. (11 - 30)

Из уравнений (11 - 16а) и (11 - 17) найдем

. (11 - 31)

Откуда

. (11 - 32)

Таким образом, методы статистической термодинамики дают возможность рассчитывать термодинамические функции по суммам по состояниям. Вычисление энтальпии, энергии Гельмгольца и энергии Гиббса не составит труда, если известны внутренняя энергия и энтропия системы.

Так как молекулы находятся одновременно в поступательном, вращательном, колебательном и др. движениях, то сумма по состояниям определяется этими составляющими. В простейших молекулах эти виды движения можно принять независимыми и возможен расчет для отдельных форм движения с использованием квантово-механических представлений.

Экспериментальной базой для вычисления сумм по состояниям служат спектры молекул.