
- •В.Н. Захарченко Курс физической химии
- •Часть 1. Химическая термодинамика
- •Предисловие
- •Основные обозначения
- •Введение
- •Системы
- •Энергия и способы ее обмена между средой и системой
- •Параметры системы. Процессы
- •Теплота. Тепловое равновесие. Нулевое начало термодинамики
- •Уравнения состояния
- •Глава 1. Первое начало термодинамики
- •Глава 2. Термохимия
- •Глава 3. Процессы с идеальным газом
- •Глава 4. Второе начало термодинамики
- •Глава 5. Характеристические термодинамические функции
- •Глава 6. Системы переменного состава. Химический потенциал
- •Глава 7. Химическое равновесие
- •Глава 8. Фазовые превращения и фазовые равновесия
- •Глава 9. Коллигативные свойства растворов и осмотические явления
- •Глава 10. Непрерывные системы
- •Глава 11. Элементы статистической термодинамики
- •Глава 12. Основные понятия термодинамики неравновесных процессов
- •Приложения
- •Предметный указатель
- •Глава 1. Первое начало термодинамики 21
- •Глава 2. Термохимия 26
- •Глава 3. Процессы с идеальным газом 39
- •Глава 4. Второе начало термодинамики 53
- •Глава 5. Характеристические термодинамические функции 72
- •Глава 6. Системы переменного состава. Химический потенциал 89
- •Глава 7. Химическое равновесие 111
- •Глава 8. Фазовые превращения и фазовые равновесия 130
- •Глава 9. Коллигативные свойства растворов и осмотические явления 165
- •Глава 10. Непрерывные системы 174
- •Глава 11. Элементы статистической термодинамики 180
- •Глава 12. Основные понятия термодинамики неравновесных процессов 194
Глава 4. Второе начало термодинамики
4 - 1. Формулировки второго начала термодинамики
Второе начало термодинамики является обобщением обширного экспериментального материала.
Из опыта известно, что для любого циклического процесса, в результате которого система совершает работу, необходимо, чтобы составные части этого процесса проводились при разных температурах.
Поясним изложенное некоторыми примерами.
При работе паровой машины может реализоваться циклический процесс, содержащий следующие стадии: нагревание воды от исходной температуры Тс до температуры кипения Тb, испарение воды при температуре кипения, адиабатическое расширение водяного пара с уменьшением его температуры до Тс, конденсация водяного пара при температуре Тс. Если бы температуры всех стадий цикла оказались одинаковыми, то работа цикла была бы равной нулю.
В двигателе внутреннего сгорания осуществляется цикл, стадии которого упрощенно можно считать следующими: адиабатическое сжатие газа от температуры Та до температуры Тb, нагревание газовой смеси в результате сгорания топлива от температуры Тb до температуры Тc, адиабатическое расширение газовой смеси до температуры Тd, выхлоп газа в атмосферу, что соответствует изобарическому уменьшению температуры до исходной Та.
При выполнении приведенных выше циклов система не только получает от внешней среды теплоту, но и отдает ее.
В частности, в цикле паровой машины нагревание воды от исходной температуры до температуры кипения сопровождается поглощением теплоты системой (теплота положительна); испарение воды происходит также при поглощении теплоты системой; конденсация водяного пара происходит при выделении теплоты системой (теплота отрицательна). В цикле двигателя внутреннего сгорания поглощению теплоты соответствует теплота, выделяющаяся при сгорании топлива, а изобарическое сжатие на последней стадии цикла сопровождается выделением теплоты системой.
Условно назовем ту часть внешней среды, от которой система получает теплоту, источником теплоты, а часть системы, которой система отдает теплоту, - стоком теплоты. Таким образом, в цикле паровой машины нагревание воды и испарение водяного пара происходит при взаимодействии системы с источником теплоты, а конденсация водяного пара - при взаимодействии со стоком теплоты. В цикле двигателя внутреннего сгорания источником теплоты служит реакция сгорания топлива, а взаимодействие системы со стоком теплоты происходит при выхлопе газа.
Анализ любого цикла, при выполнении которого совершается работа, показывает, что всегда наряду с источником теплоты имеется ее сток.
У. Томсон увидел в этом явлении, которое получило название второго закона, или второго начала, термодинамики, одно из фундаментальных свойств систем.
Невозможен циклический процесс, сопровождающийся производством работы системой, если имеется только источник теплоты (формулировка Томсона второго начала термодинамики, или постулат Томсона).
Назовем систему, совершающую работу в циклическом процессе, рабочим телом.
Примером рабочих тел могут служить газы и их смеси, пары и жидкости различных веществ.
Примем в качестве новой системы рабочее тело и источник теплоты, температура которого одинакова во всех точках.
В соответствии с постулатом Томсона циклический процесс с производством работы в такой системе невозможен. Следовательно, такая система не может уменьшать свою внутреннюю энергию в результате передачи энергии в форме работы другим системам. Заметим, что уменьшение внутренней энергии приводит к понижению температуры системы. В результате мы приходим к новой формулировке, логически связанной с постулатом Томсона:
Система, имеющая одинаковую температуру во всех точках, не может совершать работу в циклическом процессе за счет понижения своей температуры.
Описываемая система получила название perpetuum mobile II рода, невозможность реализации которого в соответствии со вторым постулатом термодинамики аналогична невозможности реализации обычного perpetuum mobile в соответствии с первым началом термодинамики.
Р.Клаузиус использовал иной подход при формулировке второго начала термодинамики.
Для понимания формулировки Клаузиуса возьмем систему, состоящую из двух частей (подсистем), имеющих разные температуры. При контакте этих частей температуры выравниваются и общая температура, которую можно вычислить по тепловому балансу, окажется меньше температуры наиболее нагретой части и больше температуры наименее нагретой части. Используя работу внешней среды, можно понизить температуру наименее нагретой части и одновременно повысить температуру более нагретой части. Именно по этому принципу работают холодильные устройства.
Опыт показывает, что без внешнего воздействия, т.е. без совершения работы извне, нельзя добиться, чтобы наименее нагретая часть системы еще больше охлаждалась, отдавая теплоту более нагретой части.
Р.Клаузиус именно это свойство систем предложил принять в качестве второго начала термодинамики.
Теплота сама по себе, т.е. без работы внешней среды, не может переходить от части системы с более низкой температурой к части системы с более высокой температурой (формулировка Клаузиуса второго начала термодинамики, или постулат Клаузиуса).
Переход теплоты от менее нагретой части системы к более нагретой означал бы, что энергия (следовательно, и температура) первой уменьшалась, а энергия и температура второй увеличивалась.
По этой причине другая формулировка, связанная с постулатом Клаузиуса, может быть выражена следующим образом:
Температура более нагретой части системы не может сама по себе, т.е. без внешней работы, повышаться за счет понижения температуры менее нагретой части.
4 - 2. Равноценность формулировок второго начала термодинамики
Предложено свыше десяти различных формулировок второго начала термодинамики. Часть из них логически связана с постулатом Томсона. Поэтому, приняв за исходный любой из этих постулатов, можно получить в качестве следствия постулат Томсона.
Внешне постулаты Томсона и Клаузиуса кажутся отдаленными друг от друга. Однако любой из них можно принять за исходный, а другой оказывается следствием. В этом заключается их равноценность (эквивалентность).
Чтобы подтвердить равноценность постулатов Томсона и Клаузиуса, используем метод доказательства от противного (reductio ad absurdum).
Доказательство состоит из двух частей: вначале доказывается, что из постулата Томсона неизбежно следует постулат Клаузиуса, а затем доказывается, что из постулата Клаузиуса неизбежно следует постулат Томсона.
Приведем это доказательство.
Предположим, что постулат Томсона всегда выполним, а постулат Клаузиуса может при каких-то условиях нарушаться. Это означает, что к системе, имеющей более высокую температуру, чем у данной, можно каким-нибудь путем без использования работы внешней среды подвести теплоту, отобранную у данной системы. В результате этих действий энергия данной системы уменьшается на величину отобранной теплоты. Далее, используя циклы с рабочим телом и систему с более высокой температурой в качестве источника теплоты, а данную систему в качестве стока теплоты, отберем поступившую к более нагретой системе теплоту. Согласно балансу энергии работа цикла и теплота, возвращенная данной системе, равны теплоте, отобранной у более нагретой системы. Таким образом, у данной системы внутренняя энергия уменьшится за счет совершенной ею работы. Более нагретая система сколько получила теплоты за счет нарушения постулата Клаузиуса, столько и отдала для осуществления циклов. Поэтому в энергетический баланс она не включается. В итоге оказывается, что данная система совершила работу за счет понижения своей энергии в циклических процессах без стока теплоты, т.е. реализован вечный двигатель второго рода, который невозможен в соответствии с постулатом Томсона. Следовательно, если выполняется постулат Томсона, то должен выполняться и постулат Клаузиуса.
Теперь предположим, что постулат Клаузиуса выполняется всегда, а при каких-либо обстоятельствах постулат Томсона может нарушаться. В этом случае можно сделать вечный двигатель второго рода и за счет понижения энергии данной системы и, следовательно, понижения ее температуры совершить работу, которая может быть получена аккумулирующей системой. Далее, найдя систему с более высокой температурой, чем у данной, можно передать ей работу из аккумулирующей системы в диссипативной форме. Например, аккумулирующая система может полученную механическую работу преобразовать в работу электризации и затем отдать ее в виде электрического тока, проходящего через проводник, погруженный в более нагретую систему, что должно повышать температуру более нагретой системы. Аккумулированную работу можно отдать более нагретой системе, используя ее для преодоления силы трения, что также приводит к повышению температуры более нагретой системы. Итогом этих действий является повышение температуры более нагретой системы за счет снижения температуры менее нагретой. Это противоречие может быть устранено, если принять, что при выполнении постулата Клаузиуса неизбежно должен выполняться постулат Томсона.
Таким образом, оба постулата эквивалентны.
4 - 3. Теорема Клаузиуса о сопряженных циклах
Теорема Клаузиуса о сопряженных циклах утверждает:
Термодинамический КПД циклов Карно, совершаемых квазистатически в данном температурном интервале, одинаков для всех систем.
Используем метод доказательства от противного.
Пусть имеются две различных системы, с каждой из которых выполняется цикл Карно в одном и том же температурном интервале. Например, такими системами могут быть вода с водяным паром и азот.
Выберем размеры (или массы) систем такими, чтобы они совершали одинаковую работу W.
Примем, что системы характеризуются следующими данными.
Условный номер системы 1 2
Теплота, получаемая от
теплового источника Q`1 Q``1
Теплота, поступающая
к тепловому стоку Q`2 Q``2
Работа цикла W=Q`1+Q`2 W=Q``1+Q``2
Термодинамический КПД
цикла ![]()
![]()
Предположим, что термодинамические КПД циклов различны, т.е.
1 2 .
Так как работа обоих циклов одинакова, то должны различаться теплоты, подводимые к системам от тепловых источников:
Q`1Q``2.
Если термодинамический КПД цикла с системой 1 больше, чем с системой 2, то теплота Q`1 окажется меньше теплоты Q``1.В этом случае пусть цикл с системой 1 выполняется в прямом направлении (как цикл двигателя), а цикл с системой 2 выполняется в обратном направлении (как холодильный цикл). Работа прямого цикла с системой 1 используется для реализации обратного цикла с системой 2, в чем и заключается сопряжение циклов. Таким образом, суммарная работа обоих циклов оказывается равной нулю. Однако в связи с тем, что теплота Q`1, поступающая от теплового источника к системе 1, меньше по абсолютной величине теплоты Q``1, возвращаемой тепловому источнику системой 2, в целом к тепловому источнику, температура которого выше температуры теплового стока, поступает теплота, равная разности этих теплот Q``1-Q`1. Из равенства работ обоих циклов следует:
Q`1+Q`2=Q``1+Q``2 ;
Q``1-Q`1=Q`2-Q``2 .
Последнее равенство означает, что тепловой сток теряет теплоту, равную теплоте, поступающей к имеющему более высокую температуру тепловому источнику.
Итак, возможность совместной реализации циклов Карно с разными термодинамическими КПД противоречит постулату Клаузиуса.
Следовательно, термодинамический КПД цикла Карно не зависит от природы рабочего тела (системы).
Ранее было показано, что для квазистатического цикла Карно, проводимого с идеальным газом, термодинамический КПД равен
,
где Т1 - температура теплового источника, а Т2 - температура теплового стока.
В соответствии с теоремой Клаузиуса эта формула применима для квазистатического цикла Карно, проводимого с любой системой.
4 - 4. Теорема Карно - Клаузиуса
Теорема Клаузиуса о сопряженных циклах позволила обобщить уравнение для КПД цикла Карно, выведенное для идеального газа, на любые системы. Дальнейшим обобщением является теорема Карно - Клаузиуса:
Из всех циклов, совершаемых квазистатически в данном температурном интервале с любыми системами, максимальным термодинамическим КПД обладает цикл Карно.
Способ доказательства теоремы Карно - Клаузиуса повторяет доказательство предварительной теоремы Карно. Он заключается в определении максимальной и минимальной температур любого цикла. Эти температуры соответствуют точкам касания изотерм с контуром произвольного цикла. Обе изотермы и две адиабаты, касающиеся произвольного цикла, определяют цикл Карно, реализуемый в том же температурном интервале, что и произвольный цикл. Далее, выделив из произвольного цикла фрагмент между двумя отстоящими на бесконечно малом расстоянии друг от друга адиабатами и заменив фрагменты произвольного цикла бесконечно малыми изотермами, сравниваются внутренние изотермы с изотермами цикла Карно, описанного вокруг произвольного цикла. Так как максимальная температура внутреннего бесконечно малого цикла Карно меньше температуры описанного цикла, а минимальная температура внутреннего цикла Карно больше минимальной температуры описанного цикла, то термодинамический КПД фрагмента произвольного цикла всегда оказывается меньше КПД цикла Карно, описанного вокруг произвольного цикла. Из этого следует, что термодинамический КПД любого произвольного цикла меньше КПД цикла Карно, проводимого в тех же температурных пределах.
4 - 5. Формулы Клаузиуса. Энтропия
Из теоремы Клаузиуса о сопряженных циклах следует, что для цикла Карно с любой системой применимо равенство
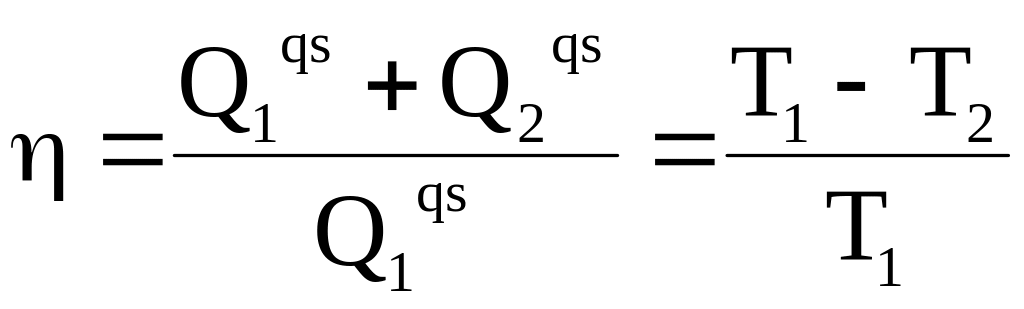 ,
,
в котором Q1qs - теплота, получаемая системой от теплового источника с температурой Т1, а Q2qs - теплота, поступающая к тепловому стоку с температурой Т2.
Таким образом, для цикла Карно с любым рабочим телом выполняется условие равенства нулю суммы приведенных теплот:
 .
.
Для бесконечно малого расстояния между адиабатами равенство принимает следующую форму:
 .
.
Обратимся к проводимому квазистатически произвольному циклу.
Обозначим точки касания адиабат с контуром произвольного цикла (1) и (2), причем (1) - левая точка касания, а (2) - правая точка касания.
Заменив произвольный цикл бесконечной суммой пар бесконечно малых изотерм, для перехода от точки (1) к точке (2) можно записать:
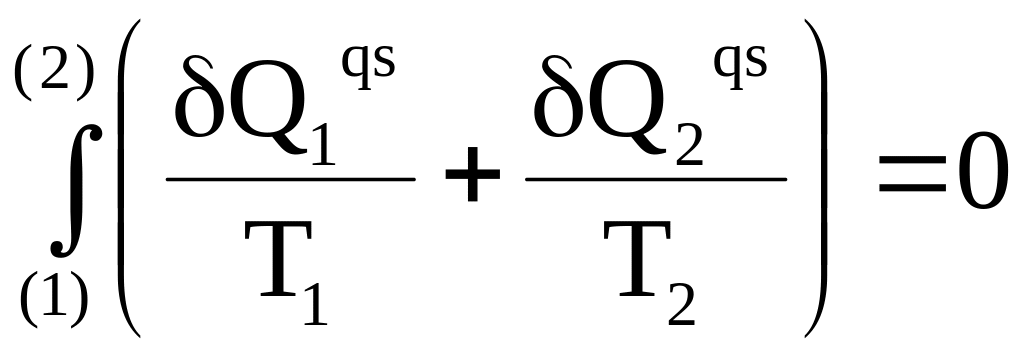 .
.
Переход от точки (1) к точке (2) по парам изотерм означает смещение слева направо по верхним изотермам и одновременное смещение справа налево по нижним изотермам. В целом это составляет перемещение по замкнутому контуру. По этой причине предыдущее равенство можно заменить следующим:
![]() . (4 - 1)
. (4 - 1)
Уравнение (4 - 1) означает, что подынтегральное выражение представляет собой приращение функции состояния. Отметим, что приращение функции состояния не зависит от процесса. Введем для новой функции обозначение S. Следовательно,
![]() . (4 - 2)
. (4 - 2)
Введенная на основе второго начала термодинамики Р.Клаузиусом функция S называется энтропией.
Энтропия обладает основными свойствами функции состояния:
приращение функции не зависит от процесса, а определяется только начальным и конечным состоянием системы,
функция аддитивна, т.е. ее величина (или приращение) представляет собой сумму энтропий (или приращений энтропии) для отдельных частей системы .
Размерность энтропии -
![]() .
.
Конечное приращение энтропии находится интегрированием
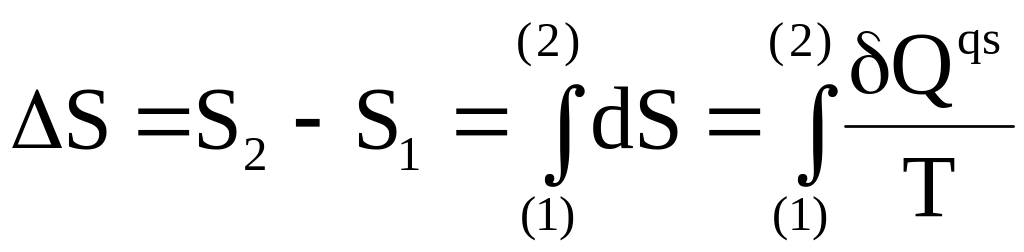 .
(4 - 3)
.
(4 - 3)
В формулах (4 - 1) - (4 - 3) используется теплота квазистатического процесса. Для нестатических (реальных ) процессов, как ранее было показано, выполняется условие
Wqs> Wr ,
из которого следует
dU+Wqs>dU+Wr,
так как приращение внутренней энергии, являющейся функцией состояния, не зависит от процесса. Поэтому
Qqs >Qr.
Следовательно,
![]() ;
(4 - 4)
;
(4 - 4)
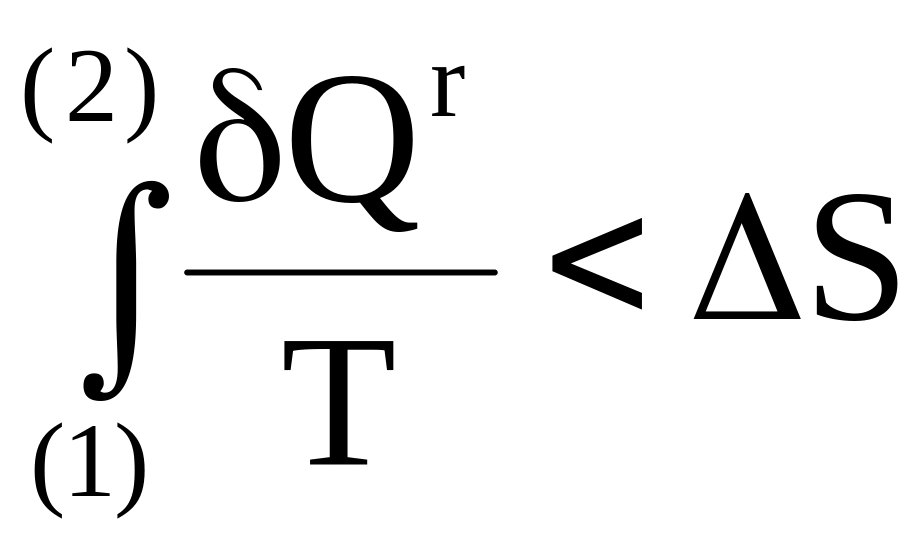 ;
(4 - 5)
;
(4 - 5)
![]() .
(4 - 6)
.
(4 - 6)
Формулы (4 - 1) - (4 - 6) называются формулами Клаузиуса.
4 - 6. Способы расчета изменения энтропии
Из формул Клаузиуса следует, что рассчитать изменение энтропии можно, если известна теплота квазистатического процесса Qqs.
Приведем примеры таких расчетов.
Изохорическое нагревание системы
Теплота, подводимая к системе, рассчитывается по формуле
Qqs=CvdT.
Бесконечно малое изменение энтропии определяется равенством
![]() .
(4 - 7)
.
(4 - 7)
Конечное приращение энтропии при нагревании системы от температуры Т1 до температуры Т2 рассчитывается по формуле
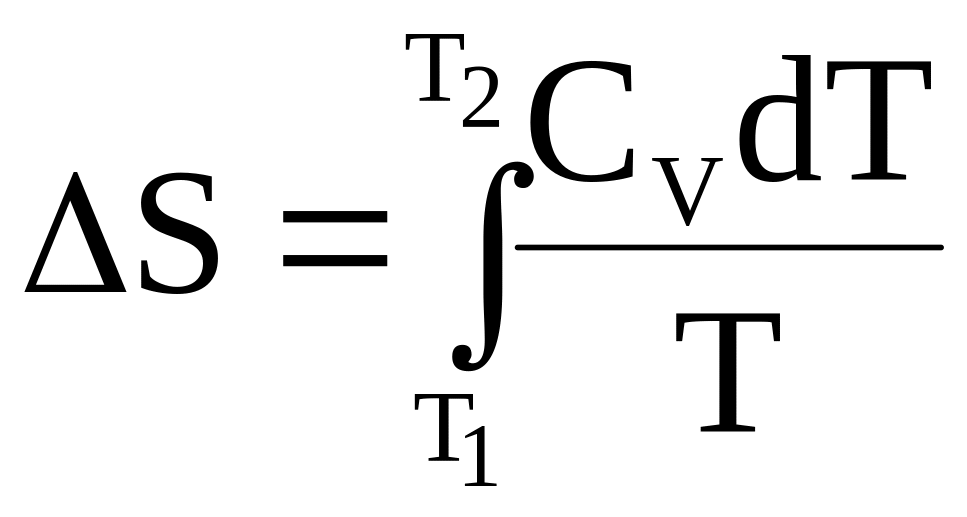 .
(4 - 8)
.
(4 - 8)
В случае постоянной теплоемкости СV интегрирование по формуле (4 - 8) дает
![]() .
(4 - 9)
.
(4 - 9)
Изобарическое нагревание системы
Теплота, подводимая к системе, рассчитывается по формуле
Qqs= CPdT. (4 - 10)
Бесконечно малое приращение энтропии определяется равенством
![]() ,
(4 - 11)
,
(4 - 11)
а конечное приращение при нагревании от температуры Т1 до температуры Т2 вычисляется по формуле
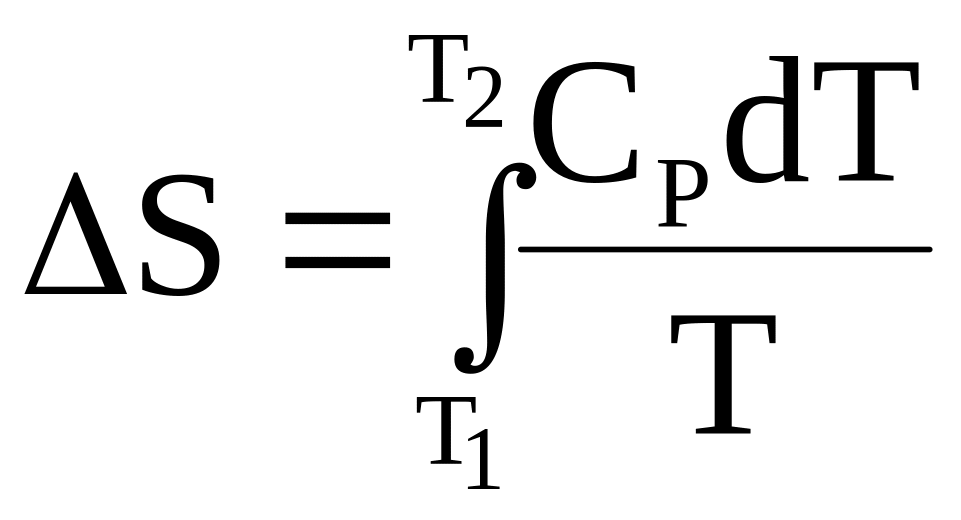 .
.
![]() (4 - 12)
(4 - 12)
Изотермическое расширение идеального газа
Теплота квазистатического расширения идеального газа равна максимальной работе расширения
![]() .
.
Бесконечно малое изменение энтропии рассчитаем по формуле
![]() .
.
Конечное приращение энтропии при изотермическом расширении 1 моль газа от объема V1 до объема V2 рассчитывается по формуле
![]() .
(4 - 13)
.
(4 - 13)
Адиабатические квазистатические процессы
При адиабатических квазистатических процессах энтропия не изменяется (S=0). По этой причине их называют изоэнтропийными процессами.
Фазовые переходы первого рода
Фазовыми переходами первого рода называют процессы изменения агрегатного состояния вещества (плавление, испарение, возгонка).
При постоянном давлении процесс фазового перехода протекает при постоянной температуре.
Изменение энтропии при фазовом переходе 1 моля вещества можно рассчитывать по формуле
![]() ,
(4 - 14)
,
(4 - 14)
в которой Hp.t. - теплота фазового перехода 1 моль, а Tp.t. - температура фазового перехода.
4 - 7. Изменение энтропии при протекании реальных процессов
По теплоте реальных процессов нельзя рассчитать изменение энтропии.
В связи с этим реальный процесс заменяется квазистатическим процессом, условно проводимым от общего для обоих процессов исходного состояния системы до общего для них конечного состояния.
Поясним изложенное примерами.
Истечение идеального газа в пустоту
Пусть в изолированной системе газ занимает первоначальный объем V1. Затем он истекает в вакуум, и его объем увеличивается до V2.
Поскольку газ изолирован от внешней среды, он не может получить теплоту извне. Истечение газа в пустоту не сопровождается работой. Следовательно, внутренняя энергия газа не изменится. В соответствии с законом Гей-Люссака - Джоуля при постоянной внутренней энергии температура также остается постоянной.
Итак, в исходном состоянии с объемом V1 и конечном состоянии с объемом V2 газ имеет одну и ту же температуру. Переход из одного из указанных состояний в другое может быть осуществлен изотермическим расширением газа в квазистатических условиях. В предыдущем параграфе было показано, что в этом случае можно воспользоваться формулой (4 - 13).
Так как конечный объем V2 больше исходного объема V1 и отношение V2/V1 больше 1, то
![]() .
.
Полученный результат означает, что изотермическое самопроизвольное расширение газа приводит к возрастанию его энтропии.
Самопроизвольное выравнивание температур
Пример 1.
Рассмотрим систему, состоящую из двух кусков металла, имеющих разные температуры Т1 и Т2. Для простоты расчетов положим, что теплоемкость обоих кусков CV одинакова и не зависит от температуры, а количество вещества в каждом куске равно 1.
При контакте обоих кусков происходит выравнивание температур и устанавливается общая для них температура Те, равная средней арифметической исходных температур:
![]() .
.
Изменение энтропии каждого куска металла выразится следующим образом:
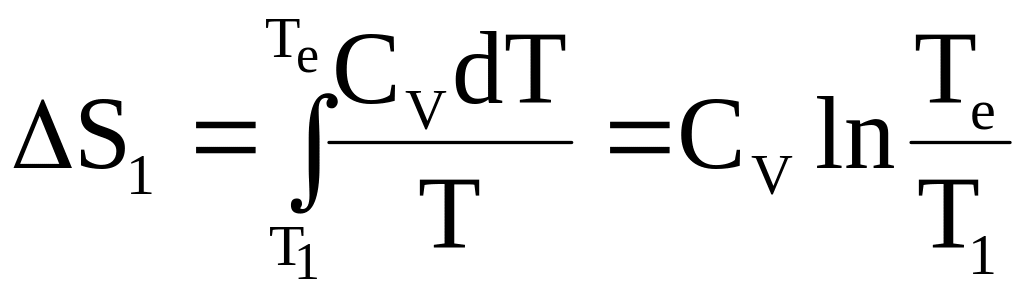 ;
;
![]() .
.
Общее изменение энтропии находим как сумму изменений для каждого куска металла (используется свойство аддитивности энтропии)
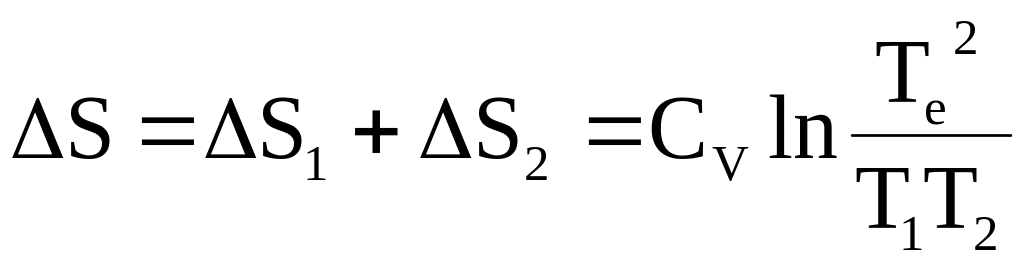 .
(4 - 15)
.
(4 - 15)
Числитель подлогарифмического выражения, как уже было показано, представляет собой квадрат средней арифметической величины от Т1 и Т2, а знаменатель - квадрат их средней геометрической. Так как средняя арифметическая величина больше средней геометрической, то
S>0.
Пример 2.
Рассчитаем изменение энтропии при добавлении к 3,6 г воды, взятой при 298 К, 27 г льда, находящегося при 273 К.
Справочные данные: теплоемкость воды Cp равна 75,3 Дж/мольК (принимается постоянной), изменение энтальпии при плавлении льда равно 6,0 кДж/моль.
Изменение энтальпии (теплота при постоянном давлении) воды при охлаждении от исходной температуры Т1=298 К до температуры плавления льда Т2=273 К рассчитывается по формуле
![]() Дж.
Дж.
Рассчитаем количество льда, которое расплавится при поглощении теплоты, выделяемой водой:
![]() моль.
моль.
Это количество меньше количества льда, имеющегося в системе, т.е. лед расплавится частично.
Изменение энтропии при плавлении льда в соответствии с формулой (4 - 14) составит
![]() Дж/ К.
Дж/ К.
Изменение энтропии воды рассчитаем по формуле (4 ‑ 12)
![]() Дж/ К.
Дж/ К.
Общее изменение энтропии находим, используя свойство аддитивности,
S=Sh +Sl=1,38+(-1,065)=0,315 Дж/ К; S>0.
Из рассмотренных примеров можно сделать вывод: при самопроизвольном выравнивании температур в системе ее энтропия возрастает.
4 - 8. Закон возрастания энтропии
Анализ любых процессов, протекающих в изолированной системе, показывает, что они возможны, если сопровождаются повышением энтропии.
Можно провести соответствующие расчеты для смешивания газов, растворения веществ и др. И во всех случаях окажется, что
процессы, протекающие в изолированной системе, всегда сопровождаются возрастанием энтропии.
Р. Клаузиус, установивший этот принцип, назвал его законом возрастания энтропии.
4 - 9. Энтропия как критерий равновесия в изолированных системах
С законом возрастания энтропии в изолированных системах связано еще одно важнейшее свойство этой функции - возможность использования ее как критерия равновесия.
Равновесие в изолированной системе означает принципиальную невозможность каких-либо изменений в ней. Поэтому в равновесной системе не могут протекать макроскопические процессы.
Любые процессы, протекающие в изолированной системе, приближают ее к состоянию равновесия. Например, в рассматривавшейся ранее системе, состоящей из двух одинаковых кусков металла при разных температурах, будет происходить выравнивание их температур, в результате чего наступит тепловое равновесие. В системе, содержащей разные газы, разделенные друг от друга, возможным процессом является смешение этих газов, что приведет к выравниванию химического состава газовой смеси.
Параллельное приближение к равновесию и возрастание энтропии происходят до того момента, когда система достигнет равновесия. Следовательно,
состоянию равновесия в изолированной системе отвечает максимум ее энтропии.
Таким образом, энтропия приобретает свойства признака, по которому можно делать оценку состояния равновесия.
Так как изолированная система характеризуется постоянством внутренней энергии и объема, то условие равновесия можно представить в следующей форме:
S=Smax при U,V=const.
Энтропия может служить критерием равновесия также при постоянной энтальпии системы и постоянном ее давлении: S=Smax при H,P=const).
4 - 10. Метод циклов в термодинамике. Уравнение Клапейрона - Клаузиуса
Метод циклов, или метод круговых процессов, оказался первым методом, с помощью которого на основании первого и второго начал термодинамики были установлены важнейшие количественные соотношения для различных явлений.
Сущность этого метода заключается в подборе подходящего квазистатического цикла, по характеристикам которого удается получить зависимость между термодинамическими величинами.
Наиболее часто в методе круговых процессов используется квазистатический цикл Карно, для которого известен термодинамический КПД.
Общих правил применения метода циклов не существует. Поэтому подбор подходящего цикла для решения какой-либо конкретной задачи является своего рода искусством.
Покажем, как применяется метод циклов на примере вывода уравнения Клапейрона - Клаузиуса, устанавливающего зависимость между параметрами системы и теплотой (изменением энтальпии) фазового перехода.
Мысленно осуществим с 1 моль вещества цикл, состоящий из следующих стадий:
фазовый переход (испарение, возгонка, плавление) при давлении Р от молярного объема исходной фазы V1 до молярного объема конечной фазы V2 (пусть, например V1 - объем жидкости, а V2 - объем пара; или V1 - объем твердого вещества, а V2 - объем жидкости и т.д.);
адиабатическое снижение давления на dP (в связи со столь незначительным изменением давления объем конечной фазы практически не изменится);
обратный переход конечной фазы в исходную (конденсация, кристаллизация) с изменением объема системы от V2 до V1;
адиабатическое сжатие системы на dP (конденсированные системы можно считать несжимаемыми, и объем системы на этой стадии не изменяется).
Контуры этого цикла в координатах (давление, объем) представляют собой узкую полоску с шириной dP и длиной (V2-V1) . Площадь этой полоски равна работе цикла
Wqs=(V2-V1)dP.
В этом цикле теплота к системе подводится только на первой стадии. Она представляет собой изменение энтальпии при фазовом переходе Hp.t..
Термодинамический КПД рассматриваемого цикла равен
![]() .
.
Данный цикл является циклом Карно (первая и третья стадии осуществляются при постоянной температуре). Если температура фазового перехода равна Т, а изменение температуры при переходе от одной изотермы к другой равно dT, то этот же КПД должен быть равен
![]() .
.
Так как левая часть обоих равенств является одной и той же величиной, то, приравнивая их правые части, получим
![]()
или
![]() . (4 - 16)
. (4 - 16)
Уравнение (4 - 16) называется уравнением Клапейрона ‑ Клаузиуса.
В процессе испарения жидкости объемом жидкости по сравнению с объемом пара можно пренебречь (для сравнения: при нормальной температуре кипения 373 К молярный объем водяного пара в 930 раз превышает объем жидкой воды). Если же предположить, что пар приближается по свойствам к идеальному газу, то можно воспользоваться следующим приближением:
![]() .
.
С учетом этого приближения уравнение Клапейрона - Клаузиуса для процессов испарения и возгонки приобретает следующую форму:
![]() .
(4 - 17)
.
(4 - 17)
Приняв теплоту испарения постоянной, интегрированием уравнения (4 - 17) можно найти зависимость давления насыщенного пара от температуры. Она обычно выражается следующим образом:
![]() ,
(4 - 18)
,
(4 - 18)
где А и В - константы, зависящие от природы вещества.
В настоящее время метод циклов употребляется редко. Его вытеснил более универсальный метод характеристических термодинамических функций, ранее называвшийся методом термодинамических потенциалов.
