36.Корреляционная функция (кф). Корреляционная функция стационарных случайных процессов. Корреляционная функция эргодических случайных процессов.

Корреляционная функция r{t, т) — детерминированная функция двух перемен­ных (времени I и сдвига во времени т). значение которой для каждой пары перемен­ных гит равно корреляционному моменту двух сечений случайного процесса — при г и t + т. Корреляционная функция определяет вероятностную взаимосвязь указанных двух сечений случайного процесса.

Указанные характеристики практически могут быть получены только экспери­ментально по выборке из достаточно большого числа (ансамбля) независимых реа­лизаций случайного процесса: получаемые таким образом приближенные данные о вероятностных характеристиках называют оценками этих характеристик. По­грешность оценок обусловлена прежде всего ограниченным объемом выборки: при увеличении объема выборки (числа обрабатываемых реализации) правильно выбранная оценка стремится к оцениваемой характеристике по вероятности (т.е. большое значение случайной погрешности становится все менее вероятным).

Оценка корреляционной функции по формуле

где = x(t) - m(t) — реализация центрированного случайного процесса = X(t) - m(t), т.е. процесса, значения которого отсчитываются от его математиче­ского ожидания.

Очевидно, что при τ = 0 значение корреляционной функции совпадает с дис­персией процесса r(t,0)=2(t)

Среди случайных процессов важный для практики класс составляют так назы­ваемые случайные стационарные процессы, т.е. процессы, вероятностные свойст­ва которых не меняются во времени. Если случайный процесс стационарен, его математическое ожидание и дисперсия не меняются во времени: mx(t)=тх =const;x2(t) = x2 = const, а корреляционная функция r(τ) не зависит от t и, следовательно, является функцией лишь одного переменного τ.

Характерный график корреляционной функ­ции стационарного процесса показан на рис. 6.2. Поскольку корреляционная функция ха­рактеризует взаимосвязь сечений процесса, она обычно представляет собой убывающую (моно­тонно или с колебаниями) функцию т, причем чем с большей частотой происходят случайные флюктуации случайного процесса, тем быстрее убывает корреляционная функция.

Убывание корреляционной функции при увеличении |τ| свидетельствует о том, что с увеличением расстояния между сечениями взаимосвязь между ними умень­шается при превышении этим интервалом некоторого предельного значения τкор, такого, что при |τ| > τкор корреляционная функция практически мало отличается от нуля (рис. 6.2), сечения случайного процесса становятся практически независи­мыми. Чем меньше интервал коррелированности τкор, тем с большей средней частотой происходят его флюктуации, тем меньшим оказывается интервал, в кото­ром сечения случайного процесса остаются зависимыми друг от друга.

Стационарные случайные процессы, как правило, обладают свойством эргодич­ности, это значит, что оценка среднего значения и корреляционной функции тако­го процесса по экспериментальным данным может проводиться усреднением не по ансамблю реализации (6.1)—(6.3), а по времени какой-нибудь одной реализа­ции: оценка математического ожидания эргодичного случайного процесса может осуществляться по формуле

x = (6.4) (где Т— длина реализации), а оценка корреляционной функции xx()=1/T∙ dt.

При = О последняя формула дает оценку дисперсии. Проведя в (6.5) замену переменных𝝃 = t + τ, получим

xx()=1/T∙

т.е. корреляционная функция стационарного процесса является четной функцией τ:

rxx(t)=rxx(–t).

Для того чтобы можно было охарактеризовать вероятностную взаимосвязь сечений двух случайных процессов, необходимо ввести взаимную корреляционную функцию этих процессов: если эта корреляционная функция зависит лишь от сдвига т, процессы называют стационарно связанными. Оценка взаимной корреляцион­ной функции эргодичных процессов ,X(t) и Ytl) может проводиться усреднением по времени:

xy()=1/T∙ dt

Если в этой формуле заменить переменную интегрирования 𝝃= t + т, можно по­лучить

()=1/T∙ (𝝃-τ)∙y0(𝝃)d𝝃=1/T∙ (𝝃)∙y0(𝝃-τ)d𝝃

т.е. видим, что взаимная корреляционная функция обладает следующим свойством:rxy(-t)=rxy(t).

Анализ систем, находящихся под воздействием случайных сигналов, обычно сводится к определению указанных вероятностных характеристик выходного сиг­нала по вероятностным характеристикам входного сигнала. Начнем с определения математического ожидания выхода стационарной динамической линейной систе­мы, когда на ее вход подается стационарный случайный сигнал X(t).

Поскольку связь между входом и выходом такой системы во временной области определяется интегралом наложения (2.55) подстановка его в формулу для оценки математического ожидания выхода у = 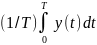дает следующий результат:

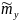()=1/T∙ 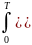(ξ)x(t–ξ)dξ]dt,или после смены порядка интегрирования

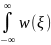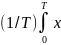()= [ (t–ξ)dt]d𝝃=hуст x где hуст =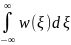 — установившееся значение переходной характеристики системы; mx — оценка математического ожидания входного воздействия. При T-> оценки математических ожиданий сходятся по вероятностям к истинным значениям, что позволяет записать: my= hустmx(6.9)

Например, математическое ожидание сигнала на выходе инерционного звена, переходная характеристика которого определяется (3.10), равно кшя (где к — коэф­фициент передачи звена), а на выходе реального дифференцирующего звена, пере­ходная характеристика которого определяется (3.8), равно нулю.

Подобным же образом может быть получено выражение для корреляционной функции выхода линейной динамической системы. Так как

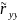()=1/T∙ 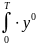(t)∙y0(t+)dt=1/T∙ (ξ)x0(t–ξ)dξ]∙[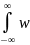 (η)x0(t+–η)dη]dt

После смены порядка интегрирования:

()= (ξ){ (η)∙[1/T∙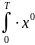 (t–ξ)∙x0(t+–η)dt]dη} dξ

Заметим:

1/T∙ (t–ξ)∙x0(t+–η)dt=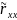 (+ξ–η).

Итак, корреляционная функция вых. Сигнала

()= (ξ)∙ (η)∙ (+ξ–η)dη dξ.

Взаимная корреляционная функция входной и выходной величин системы рис. 6.3, а) может быть получена подстановкой в (6.7) интеграла наложения:

()=1/T∙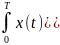 (ξ)x(t+τ–ξ)dξ]dt

который после смены порядка интегрирования имеет вид

()= (ξ) (τ–ξ)dξ

Переходя от оценок к самим корреляционным функциям, получаем:

rxy ()= (ξ)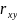 (τ–ξ)dξ

Таким образом, взаимная корреляционная функция входной и выходной вели-ин линейной динамический системы связана с корреляционной функцией входа бычным интегралом свертки.

Рассмотрим случай, когда на вых. сигнал наложена помеха,независимая от вх. возд. my=hуст·mx+mn;

ry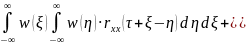y( )= rnn( ). rxy( )= .

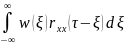Использование преобразования Фурье позволяет упростить определение взаимн. кор. ф-ции СП на вх. в лин. динамич. сис-му и выходе из нее. Применив к (1) это преобразование, получим:

Gxy(iω)=W(iω)·Gxx(iω); где Gxy(iω)= .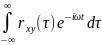

Фурье-изображение взаимной корреляционной ф-ции 2 случ. процессов – взаимная спектральная плотность мощности 2 случ. процессов.

G-xy(s) и G+xy(s) для Gxy(s) не равны друг другу.

Взаимн. спектр. пл-ть явл. комплексной ф-цией частоты. Если поменять знак:

Gxy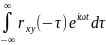(iω)= , то Gxy(iω)= Gyх(-iω).