36. Резонанс в цепи с двумя параллельными ветвями

Н а рис. 7.12 а (показана схема параллельного соединения двух ветвей R₁, L и R₂, С. В такой схеме возможен резонанс токов. На рис. 7.12 б показана векторная диаграмма данной схемы в режиме резонанса токов. На диаграмме отмечено, что вектор общего тока совпадает по направлению с вектором приложенного напряжения , т. е. эти векторы совпадают по фазе, что и свойственно режиму резонанса. Входная комплексная проводимость

.

При резонансе токов b = 0, т. е. .

Как видно из последней формулы, резонанс может быть достигнут изменением одной из величин , L, С, R₁, R₂. Однако этот режим не всегда может быть получен, а именно, когда значение изменяемой величины (при заданных остальные четырех величинах) получается при решении последнего уравнения мнимым или комплексным. Для L и С могут быть получены и по два вещественных значения. В таком случае могут быть получены два резонансных режима.

Решая последнее уравнение относительно а, найдем следующее значение для резонансной частоты

Д ля получения вещественного значения необходимо, чтобы сопротивления R₁ и R₂ были оба или меньше или оба больше, чем .

Если R₁ = R₂ = 0, то (идеальный контур).

Если , то резонанс будет иметь место при любой частоте, так как в этом случае получается неопределённость .

37. Резонансные кривые параллельного контура

Д ля идеального параллельного контура (когда R₁ = R₂ = 0) резонансная кривая показана на рис. 7.13. При этом и резонансная частота .

В ходное сопротивление идеального параллельного контура при резонансе равно бесконечности, , поэтому при резонансной частоте общий ток равен нулю. Однако токи в ветвях и существуют, они одинаковые по модулю и противоположны по фазе (см. рис. 7.12 б).

На рис. 7.14 приведена резонансная кривая реального контура. Эта кривая может быть рассчитала по формуле

А.

35. Добротность. Влияние добротности на резонансные кривые последовательного контура r ,l, с

Любой резонансный контур, в том числе и последовательный принято характеризовать добротностью Q и характеристическим сопротивлением .

Напомним, что в данном случае будем рассматривать определение добротности контура при изменении частоты источника питания.

При резонансе .

Добротность контура определяет кратность превышения напряжения на зажимах индуктивного или емкостного элемента сопротивления при резонансе над напряжением всей цепи U = U_R.

В электротехнических и радиотехнических установках добротности могут быть любого порядка, вплоть до десятков тысяч. При больших добротностях (50–500) U_L0 >> U_R, U_R = U_ВХ = U, т. е. напряжение на индуктивности (или на емкости) во много раз больше приложенного напряжения.

Выясним влияние добротности на резонансные кривые при последовательном соединении R, L, С. Ток в цепи равен

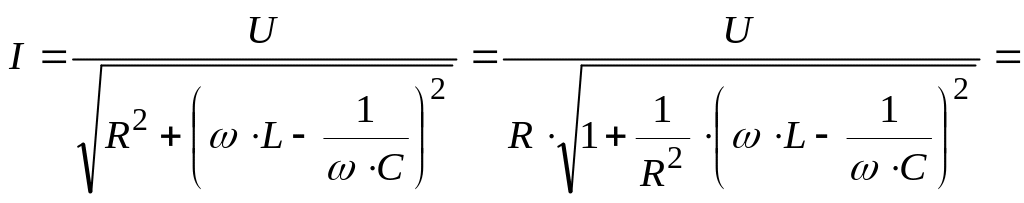
Относительное значение тока: , т.е. .

Пои выводе этой формулы учитывалось, что .

Иногда вводят понятие относительной частоты .

Тогда предыдущая формула запишется так

Построим резонансные кривые в относительных (по току) единицах (рис. 7.8) для трех добротностей. Рассматривая три резонансные кривые, видим, что чем больше добротность, тем острее получается резонансная кривая. Полоса пропускания контура определяется разностью частот, которые получатся при пересечении резонансной кривой горизонтальной линией на уровне .

Из рис. 7.8 видно, что чем меньше добротность, тем шире полоса пропускания. В радиоприемниках колебательные контуры имеют большие добротности (500–1000), поэтому эти контуры обладают достаточно узкими полосами пропускания, что способствует избирательному радиоприему только одной станции.