
- •2. Закон Ома для участка цепи с эдс
- •3. Баланс мощности в электрической цепи
- •4 . Применение законов Кирхгофа к расчету электрических цепей
- •5 . Метод узловых потенциалов
- •6 . Метод контурных токов
- •7. Матричная форма записи законов Ома и Кирхгофа
- •8. Матричная форма записи метода контурных токов
- •9. Матричная форма записи метода узловых потенциалов
- •10.Преобразование пассивного треугольника сопротивлений в звезду и обратно
- •1 2. Эквивалентные схемы источников энергии
- •14. 1)Линейные соотношения в линейных электрических цепях
- •15. Теорема о компенсации
- •1 6. Метод эквивалентного генератора
- •17. Синусоидальный ток
- •2) Изображение синусоидальных функций времени векторами и комплексными числами на комплексной плоскости
- •18. Электрическая цепь синусоидального тока и ее схема
- •20. Ток и напряжение при последовательном соединении r, l, с
- •21. Изображение синусоидальных функций времени векторами и комплексными числами на комплексной плоскости
- •22. Комплексное сопротивление
- •24. Ток и напряжения при параллельном соединении r, l, с
- •25. Комплексная проводимость
- •26. Пассивный двухполюсник
- •27. Мощность в цепи синусоидального тока
- •31. Резонанс напряжений в цепи r, l, с
- •36. Резонанс в цепи с двумя параллельными ветвями
- •35. Добротность. Влияние добротности на резонансные кривые последовательного контура r ,l, с
- •34.Идеальный трансформатор
- •41.Эквивалентная замена (развязка) индуктивных связей
- •40.Разветвленная цепь с индуктивными связями
- •39.Взаимная индуктивность
- •46. Мощность трехфазной цепи. Измерение активной мощности в трехфазных цепях
- •47. Метод имметричных составляющих10.1. Общие и методические замечания
- •Разложение трехфазной несимметричной системы векторов на три трехфазные симметричные системы векторов
- •48. Применение метода симметричных сосгавляющих для расчета трехфазной цепи с несимметричной системой эдс генератора
- •51.Цепи несинусоидального токаОбщие и методические замечания
- •59.Мощность в цепи периодического несипусоидального тока
- •.57. Расчет цепей с несинусондальиыми напряжениями и токами
- •60.Высшие гармоники в трехфазных цепях
25. Комплексная проводимость
Комплексной проводимостью называется отношение комплексного тока к комплексному напряжению

где
![]() – величина, обратная полному сопротивлению
и называемая полной проводимостью.
– величина, обратная полному сопротивлению
и называемая полной проводимостью.
Комплексная
проводимость и комплексное сопротивление
взаимно обратны. Комплексную проводимость
можно представить в виде
![]() где
где
![]() –
вещественная
часть комплексной проводимости,
называется активной проводимостью.
–
вещественная
часть комплексной проводимости,
называется активной проводимостью.
![]() – значение мнимой части комплексной
проводимости, называется реактивной
проводимостью. При этом
– значение мнимой части комплексной
проводимости, называется реактивной
проводимостью. При этом
![]()
Для
схемы, представленной на рис. 5.7,
комплексная проводимость
![]()
Где
![]() и
называются соответственно активной,
индуктивной и емкостной проводимостями.
и
называются соответственно активной,
индуктивной и емкостной проводимостями.
Реактивная проводимость b = bL – bC.
Индуктивная (bL) и емкостная (bC) проводимости – арифметические величины, а реактивная проводимость (b) - алгебраическая величина и может быть как больше, так и меньше нуля, или равна нулю. Реактивная проводимость в ветви, содержащей только индуктивность, равна индуктивной проводимости bL, а реактивная проводимость в ветви, содержащей только емкость, равна емкостной проводимости с обратным знаком, т. е. – bC. Единица проводимости – Сименс (См).
26. Пассивный двухполюсник
Пассивный двухполюсник (см. рис. 5.11 справа) может быть представлен двумя эквивалентными схемами.
Первая схема представляет собой последовательное соединение активного и индуктивного элементов (рис. 5.12); вторая – параллельное соединение элементов только с активной и реактивной проводимостями (рис. 5.13).
Если известны параметры первой схемы, то по ним можно определить параметры второй и наоборот.
Пусть
известно
![]()
Тогда
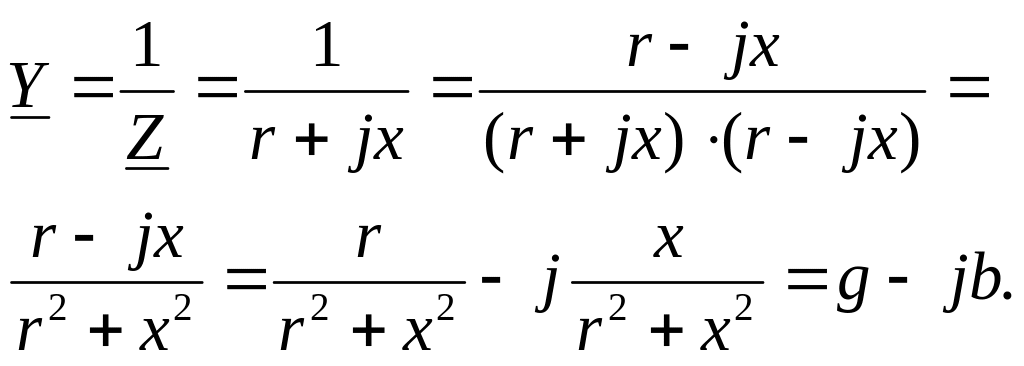
итак
![]()
Пусть
известна
![]()
Тогда

Откуда
![]()
Следует обратить внимание на то, что мнимая часть комплексной проводимости, имеющая индуктивный характер всегда отрицательна, а емкостная – положительна. И еще одно существенное замечание.
При переходе от последовательной схемы замещения к параллельной оказывается, что активная проводимость g зависит не только от активного сопротивления r, но и от реактивной составляющей полного сопротивления x = L, т. е. зависят от частоты; реактивная проводимость b зависит и от величины r. То же самое можно сказать и о переходе от параллельной схемы замещения к последовательной.
Переход от одной схемы замещения к другой не изменяет величину напряжения и тока на входе пассивного двухполюсника. Реактивное сопротивление пассивного двухполюсника (рис. 5.11) может быть или индуктивное, или емкостное. Поэтому на эквивалентной схеме (рис. 5.12) сопротивление х показано условно прямоугольником.
Напряжение
можно разложить на составляющие
![]()
где
![]() – составляющая, совпадающая по фазе с
током, называется активной составляющей
напряжения;
– составляющая, совпадающая по фазе с
током, называется активной составляющей
напряжения;
![]() – составляющая,
сдвинутая по фазе относительно тока на
угол /2,
называется реактивной составляющей
напряжения.
– составляющая,
сдвинутая по фазе относительно тока на
угол /2,
называется реактивной составляющей
напряжения.
Составляющие
![]() и
и
![]() можно рассматривать как напряжения на
элементах r
и
х
эквивалентной схемы. На рис. 5.14 а
представлена векторная диаграмма
двухполюсника (pиc.
5.11) для случая, когда
> 0, т. е. х
– индуктивное
сопротивление.
можно рассматривать как напряжения на
элементах r
и
х
эквивалентной схемы. На рис. 5.14 а
представлена векторная диаграмма
двухполюсника (pиc.
5.11) для случая, когда
> 0, т. е. х
– индуктивное
сопротивление.
Т реугольник,
образованный векторами
,
,
,
со сторонами, пропорциональными z,
r
и |x|,
называется треугольником напряжений.
Подобный ему треугольник, стороны
которого в произвольно выбранном
масштабе равны сопротивлениям z,
r
и |x|
(рис. 5.14б),
называется треугольником сопротивлений.
реугольник,
образованный векторами
,
,
,
со сторонами, пропорциональными z,
r
и |x|,
называется треугольником напряжений.
Подобный ему треугольник, стороны
которого в произвольно выбранном
масштабе равны сопротивлениям z,
r
и |x|
(рис. 5.14б),
называется треугольником сопротивлений.
Из треугольника напряжений следует, что
![]()
Другая эквивалентная схема того же двухполюсника, состоящая из параллельного соединения проводимостей g и b, показана на рис. 5.13. Поскольку в общем проводимость b может быть или индуктивной, или емкостной, на эквивалентной схеме она изображается условно прямоугольником (рис. 5.13). Ток на входе двухполюсника (рис. 5.13) можно разложить на составляющие
![]()
где
![]() – составляющая, совпадающая то фазе с
напряжением, называется активной
составляющей тока;
– составляющая, совпадающая то фазе с
напряжением, называется активной
составляющей тока;
![]()

 – составляющая,
сдвинутая по фазе относительно напряжения
на угол /2,
называется реактивной составляющей
тока; напомним: в нашем случае для
пассивного двухполюсника (рис. 5.11)
принято, что х
– индуктивное
сопротивление. Составляющие
– составляющая,
сдвинутая по фазе относительно напряжения
на угол /2,
называется реактивной составляющей
тока; напомним: в нашем случае для
пассивного двухполюсника (рис. 5.11)
принято, что х
– индуктивное
сопротивление. Составляющие
![]() и
и
![]() можно рассматривать как токи в элементах
g
и b
эквивалентной схемы.
можно рассматривать как токи в элементах
g
и b
эквивалентной схемы.
Треугольник, образованный векторами , и (рис. 5.15 а) со сторонами, пропорциональными у, g, |b|, называется треугольником токов. Подобный ему треугольник, стороны которого в произвольно выбранном масштабе равны проводимостям у, g b, называется треугольником проводимостей (рис. 5.15 б).
Из
треугольника токов имеем
![]()

