20. Ток и напряжение при последовательном соединении r, l, с

Пусть в схеме рис.5.3, состоящей из последовательно соединенных сопротивления R, индуктивности L, емкости С, известен ток При последовательном соединении сопротивлений ток, протекающий через каждый элемент, имеет одно и то же значение.

Уравнение для этой цепи имеет вид

Подставим значение тока в это уравнение

Из полученных выражений для u_r, u_L, u_C видно, что напряжение на сопротивлении r совпадает по фазе с током, напряжение на индуктивности опережает ток по фазе на угол /2, а напряжение на емкости отстает по фазе от тока на угол /2.

На рис. 5.4 показаны кривые мгновенных значений тока и напряжений для частного случая, когда амплитуда напряжения та катушке больше амплитуды напряжения на конденсаторе и _i > 0. Синусоида и_r совпадает по фазе с синусоидой тока, а синусоиды и_L и и_С сдвинуты относительно тока на угол /2 соответственно влево (опережение) и вправо (отставание). Ордината кривой напряжения состоит из суммы ординат кривых и_r + и_L + и_C = и. Запишем комплекс действующего значения тока и комплексы действующих значений напряжений на основании выражений для мгновенного тока и мгновенных напряжений: где действующее Значение тока

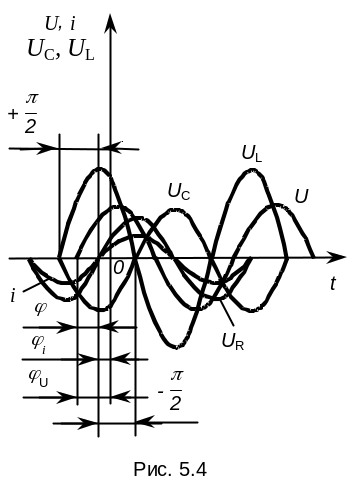
В выражениях для и учтено, что

Сумме синусоидальных напряжений соответствует сумма изображающих их векторов или комплексов их действующих значений напряжений

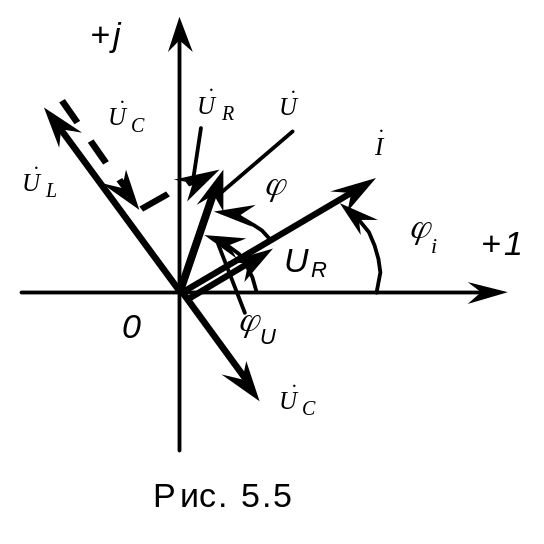
Это соотношение представляет собой уравнение по второму закону Кирхгофа, записанное в комплексной или векторной форме. Представим его на векторной диаграмме рис. 5.5. Напряжение u_r соответствует по фазе с током i, поэтому вектор изобразим одинаково направленным с вектором . Напряжение u_L опережает по фазе i на /2, поэтому вектор сдвинем относительно вектора на угол /2 «вперед» (против направления движения часовой стрелки). Напряжение u_C отстает по фазе от i на /2, поэтому вектор сдвинем относительно вектора на угол /2 «назад» (по направлению движения часовой стрелки). Эти соображения о взаимном расположении векторов напряжения и тока непосредственно следуют из записи выражений комплексных напряжений , , и тока .

Действительно, вектор получается умножением на вещественную величину r. Аргумент комплексной величины такой же, как комплексного тока , поэтому направление вектора совпадает с направлением вектора . Вектор получается умножением на . Умножение тока на вещественную величину не изменяет аргумента, а умножение на увеличивает аргумент на /2. Следовательно, вектор повернут относительно вектора на угол /2 «вперед». Вектор получается делением на . Деление комплексной величины на не изменяет аргумента, а деление на j, что равносильно умножению на , уменьшает аргумент на /2. Следовательно, вектор повернут относительно вектора на угол /2 «назад».

Так как умножение и деление вектора на j приводят к повороту вектора на /2 соответственно «вперед» и «назад», то множитель j часто называют оператором поворота на /2. Сложив векторы , и , получим вектор . Его длина определяет действующее напряжение , а положение относительно координатных осей – начальную фазу _u.

Решим, ту же задачу аналитически. Напомним, что был задан ток . На основании последних выкладок можно записать:

Или

где – комплексное сопротивление.

Это соотношение между комплексными напряжениями и током называют законом Ома в комплексной форме. Записав комплексные величины в показательной форме, имеем

Где

Получаем

Заметим

Так как и то

Таким образом, амплитуда U_m и начальная фаза _u напряжения на зажимах цепи определены, и можно записать выражение для мгновенного напряжения