Задание автомата в виде графа переходов и выходов.
Г
раф
автомата – ориентированный связный
граф. Вершины соответствуют состояниям
автомата, а дуги - переходу из состояния
a(t) в состояние
a(t+1): aS=f(am,
xj)
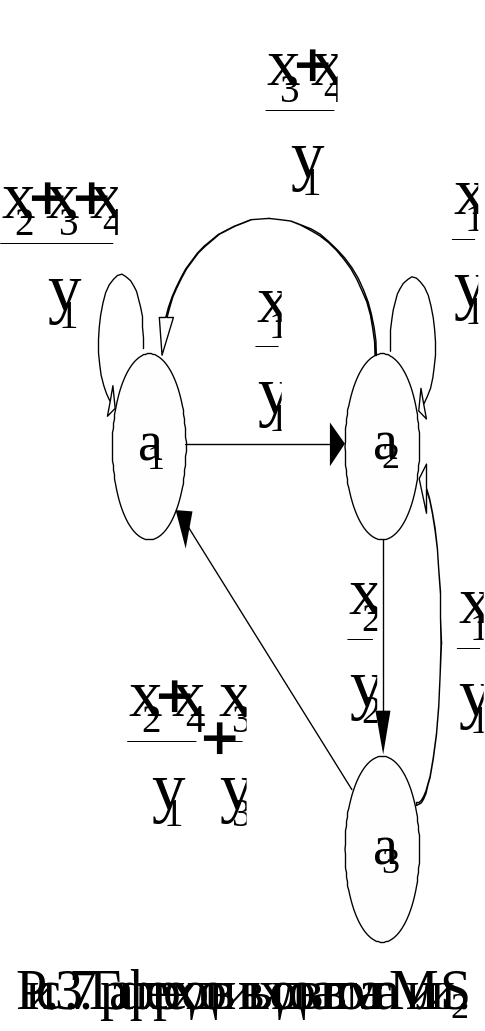
Изображения графов для автоматов Мура и Мили имеют отличительные особенности (рис. 3.4. и 3.5). У автомата Мура выходной сигнал записывается внутри вершины или рядом с ней, а у автоматов Мили над дугой: или у её конца, при этом входной сигнал изображается в начале дуги, или под входным сигналом. Тогда входной и выходной сигналы отделяются чертой.
Пример 3.1.
На рис. 3.6. и 3.7. приведены графы эквивалентных автоматов Мура S1 и Мили S2, определённых на алфавитах x={x1,x2,x3,x4} и y={y1,y2,y3}. Эти автоматы на любую входную последовательность, оканчивающуюся на x1x2(… x1x2), формируют выходной сигнал y2 (… y2), а на x1x2x3 (… x1x2x3) сигнал y3 (… y3). Говорят, что автоматы распознают последовательности x1x2 или x1x2x3. Назовём их правильными. Если входные символы не образуют правильной последовательности или пришли не все символы правильной последовательности формируется выходной сигнал y1.
Задание автомата в виде таблиц переходов и выходов.
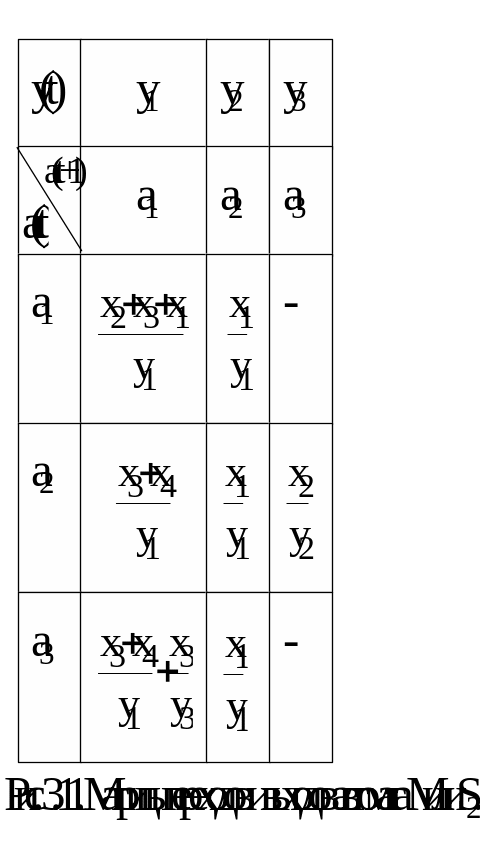
Описание автоматов в виде таблиц демонстрируется рис. 3.8. и 3.9, где изображены таблицы переходов и выходов эквивалентных автоматов Мура S2 и Мили S2, графы которых приведены на рис. 3.6 и 3.7.
Строки этих таблиц соответствуют входным сигналам, а столбцы – состояниями, причём крайний левый столбец состояний обозначен начальным состоянием a1. В таблице переходов внутренняя клетка, находящаяся на пересечении строки и столбца, соответствует состоянию перехода a(t+1).
Для автомата Мили таблица выходов совмещены с таблицей переходов: над чертой в клетке записывается состояние а(t+1), a под ней – выходной сигнал y(t).
Задание автомата в виде матриц переходов и выходов.
Задание автоматов в виде матриц демонстрируется на рис. 3.10 и 3.11, где изображены матрицы рассмотренных выше автоматов S1 и S2.
Матрица переходов является квадратной матрицей.
Матрицы переходов и выходов имеют теоретическое значение, и используется при изучении поведения абстрактных автоматов.
Табличная форма представления матриц переходов и выходов.
На практике часто используется табличная форма представления матриц (рис. 3.12 и 3.13)
3.2.3. Минимизация числа внутренних состояний абстрактных автоматов.
Сущность метода минимизации числа внутренних состояний некоторого исходного автомата заключается в разбиении всего его алфавита внутренних состояний на попарно не пересекающиеся классы эквивалентных состояний с заменой далее каждого класса эквивалентности одним состоянием. Получающийся в результате минимальный автомат имеет столько же состояний, на сколько классов эквивалентности разбивается все множество внутренних состояний заданного автомата.
Эквивалентными называются такие два состояния автомата, замена которых одно на другое не изменяет результатов словарного преобразования на всем множестве допустимых входных слов. Можно говорить как о полной эквивалентности внутренних состояний (для входных слов неограниченной длины), так и о k-эквивалентности состояний (для слов длиной в k символов). В дальнейшем классы эквивалентных и k-эквивалентных внутренних состояний будут соответственно обозначаться как П и Пk .
Процедура минимизации числа внутренних состояний абстрактного автомата состоит из следующих шагов:
1. Находятся последовательные разбиения П1 , П2 ,…, Пk алфавита внутренних состояний на классы одно-, двух-, …, k-эквивалентных состояний, до тех пор, пока на каком-то k+1-м шагом не окажется, что Пk+1= Пk . Очевидно, что при достижении этого тождества можно утверждать, что Пk= П , т.е. что k-эквивалентные состояния являются полностью эквивалентными. Нетрудно увидеть, что число шагов этой процедуры не может превысить значения l -1, где l -размеры алфавита внутренних состояний автомата.
2. В каждом классе эквивалентности П выбирается по одному символу, которые и составляют новый алфавит внутренних состояний минимизированного автомата.
3. Таблицы выходов и переходов минимизированного автомата получаются из таблиц исходного автомата путем вычеркивания столбцов с состояниями, не вошедшими в минимизированный алфавит, и замены в оставшихся столбцах внутренних состояний исходного автомата эквивалентными им состояниями минимизированного автомата.
4. В качестве начального состояния автомата выбирается или начальное состояние исходного автомата, или любое ему эквивалентное.
Рассмотрим пример минимизации автомата Мили, заданного совмещенной таблицей переходов и выходов (табл. 3.1.).
Таблица 3.1.
Xi |
a k |
|||||||||||
a 1 |
a 2 |
a 3 |
a 4 |
a 5 |
a 6 |
a 7 |
a 8 |
a 9 |
a 10 |
a 11 |
a 12 |
|
X1 |
a 10 Y1 |
a 12 Y1 |
a 3 Y2 |
a 7 Y2 |
a 3 Y1 |
a 7 Y2 |
a 3 Y1 |
a 10 Y1 |
a 7 Y2 |
a 1 Y2 |
a 5 Y2 |
a 2 Y2 |
X2 |
a 5 Y2 |
a 7 Y2 |
a 6 Y1 |
a 11 Y1 |
a 9 Y2 |
a 11 Y1 |
a 6 Y2 |
a 4 Y2 |
a 6 Y1 |
a 8 Y1 |
a 9 Y1 |
a 8 Y1 |
Класс П1 выделяется из табл. 3.1. путем объединения тех внутренних состояний, которые характеризуются одинаковой реакцией на слова длиной в один символ. Заметим, что в понятие реакции входит только выходной сигнал, поскольку основным назначением автомата является осуществление словарного преобразования. Для класса П1 выполняются:
П1 ={ A 1 1, A 2 1}; A 1 1={ a 1, a 2, a 5, a7, a8}; A 2 1={ a3, a4, a6, a9, a10, a11, a12}.
Строим таблицу П1 (табл. 3.2.), получая ее из совмещенной таблицы заменой символов исходного алфавита внутренних состояний на классы 1-эквивалентности.
Очевидно, что любая пара 1-эквивалентных состояний будет и 2-эквивалентна, если они любым входным сигналом будут переводиться в 1-эквивалентные. Практически это означает, что 2-эквивалентными будут те состояния, которые уже входя в тот или иной класс эквивалентности, в данной таблице имеют одинаковые столбцы. Тогда по табл. 3.2. для класса П2 получаем: П2 ={ A 1 2, A 2 2, A 3 2, A 4 2}; A 1 2={ a1, a2};
A 2 2={ a5, a7, a8}; A 3 2={ a3, a4, a6, a9, a11}; A 4 2={ a10, a12}
Таблица 3.2.
Xi |
ak, A sp |
|||||||||||
A 11 |
A 12 |
|||||||||||
a1 |
a2 |
a5 |
a7 |
a8 |
a3 |
a4 |
a6 |
a9 |
a10 |
a11 |
a2 |
|
X1 |
A 12 |
A 12 |
A 12 |
A 12 |
A 12 |
A 11 |
A 11 |
A 11 |
A 11 |
A 11 |
A 11 |
A 11 |
X2 |
A 11 |
A 11 |
A 12 |
A 12 |
A 12 |
A 12 |
A 12 |
A 12 |
A 12 |
A 11 |
A 12 |
A 11 |
Таблица 3.3.
Xi |
ak, A sp |
|||||||||||
A 21 |
A 22 |
A 23 |
A 24 |
|||||||||
a1 |
a2 |
a5 |
a7 |
a8 |
a3 |
a4 |
a6 |
a9 |
a11 |
a10 |
a12 |
|
X1 |
A 24 |
A 24 |
A 23 |
A 23 |
A 24 |
A 22 |
A 22 |
A 22 |
A 22 |
A 22 |
A 21 |
A 21 |
X2 |
A 22 |
A 22 |
A 23 |
A 23 |
A 23 |
A 23 |
A 23 |
A 23 |
A 23 |
A 23 |
A 22 |
A 22 |
Таблица 3.4.
Xi |
ak, A sp |
|||||||||||
A 31 |
A 32 |
A 33 |
A 34 |
A 35 |
||||||||
a1 |
a2 |
a5 |
a7 |
a8 |
a3 |
a4 |
a6 |
a 9 |
a 11 |
a 10 |
a 12 |
|
X1 |
A 35 |
A 35 |
A 32 |
A 32 |
A 34 |
A 33 |
A 33 |
A 33 |
A 33 |
A 33 |
A 31 |
A 31 |
X2 |
A 32 |
A 32 |
A 34 |
A 34 |
A 34 |
A 34 |
A 34 |
A 34 |
A 34 |
A 34 |
A 33 |
A 33 |
Продолжая аналогичную процедуру и далее, соответственно получим класс эквивалентности П3. Таблицы для всех этих классов: для П2 - табл. 3.3., для П3 - табл. 3.4.
Из табл. 3.5. видно, что П3 = П, откуда можно составить совмещенную таблицу уже минимизированного автомата (табл. 3.5.).
Используя рассмотренную процедуру по отношению к автомату, представленному графом на рис. 3.14., легко показать, что тот автомат после минимизации полностью переходит в автомат Мили, граф которого помещен на рис. 3.15.
Аналогичную процедуру минимизации можно провести и для автомата Мура.
Таблица 3.5.
Xi |
a k |
||||
a 1 |
a 5 |
a 8 |
a 3 |
a 10 |
|
X1 |
a 10 Y1 |
a 3 Y1 |
a 10 Y1 |
a 5 Y2 |
a 1 Y2 |
X2 |
a 5 Y2 |
a 3 Y2 |
a 3 Y2 |
a 3 Y1 |
a 8 Y1 |
Рис. 3.14. Рис. 3.15.