Марковський процес, що описує смо змішаного типу з обмеженим часом очікування в черзі
СМО складається з n
каналів обслуговування. Починаючи з
моменту часу
на вхід СМО поступає найпростіший потік
заявок з інтенсивністю λ.
Якщо є вільні канали, то заявка починає
обслуговуватись одним каналом, якщо
всі канали зайняті, то заявка стає в
чергу і очікує обслуговування не більше
ніж
одиниць часу. Якщо за цей час заявка не
почне обслуговуватись, то вона покидає
СМО, тобто отримує відмову. Час очікування
будемо вважати випадковою величиною,
що має показниковий закон розподілу з
параметром
,
тобто
.
Отже, в середньому заявки
будуть очікувати початок обслуговування
одиниць часу.
Завдяки властивості післядії показникового розподілу, для кожної заявки закон розподілу часу очікування, що залишився, не залежить від того, як довго ця заявка вже знаходиться в черзі.
Дисципліна обслуговування найпростіша. Час обслуговування Т має показниковий закон розподілу з параметром μ, причому будемо вважати, що час обслуговування даної заявки не залежить від часу обслуговування інших заявок та від інших заявок, що поступають.
Робота СМО описується випадковим процесом – кількістю заявок в системі в момент часу t. Частина цих заявок може обслуговуватись, інші очікують обслуговування в черзі. Можливими значеннями цього процесу є числа 0, 1, 2, … , n, ... . Так само, як в попередніх розділах, неважко переконатись в тому, що випадковий процес є однорідним ланцюгом Маркова з дискретною множиною значень і неперервним часом.
Якщо , тобто в момент часу t в системі знаходиться k заявок, то будемо вважати, що система знаходиться в стані . Позначимо через ймовірність того, що в момент часу t система знаходиться в стані , тобто
.
Позначимо через перехідну ймовірність, тобто ймовірність того, що за час система перейшла із стану в стан . Асимптотичні формули для при такі самі, як і для СМО з чергами. При формули будуть відрізнятись.
Знайдемо спочатку ймовірність того, що одна заявка за час не дочекається початку обслуговування і покине СМО. Очевидно, що ця ймовірність дорівнює:
.
Оскільки заявки незалежні
одна від одної, то ймовірність того, що
за час
з s
заявок, що знаходяться в черзі, рівно
l (
покинуть систему можна шукати за
біноміальною формулою:
.
Звідси випливає, що
,
,
.
Знаходимо тепер перехідні ймовірності . Із стану в стан за час можна перейти наступним чином:
в систему за час надійшла одна заявка (ймовірність див. глава ІІ), жоден з n каналів не звільнився (ймовірність
див. глава ІІ) і жодна заявка з черги не
покинула систему не обслугованою
(ймовірність
;в систему за час надійшли l (l ≥ 2) заявки (ймовірність
),
s
каналів з n
каналів звільнилися (ймовірність
)
і
заявки покинули чергу без обслуговування
(ймовірність
).
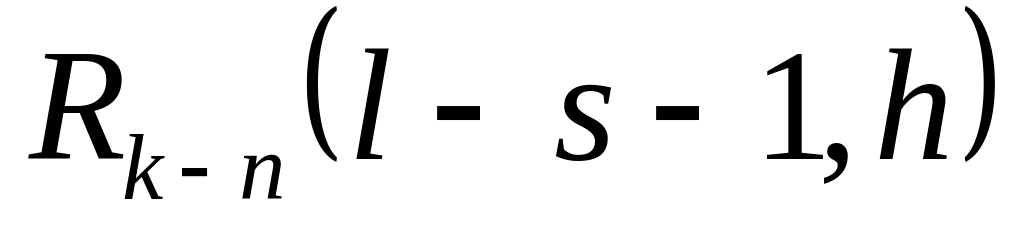Отже ймовірність дорівнює:
Із стану в стан за час можна перейти наступним чином:
в систему за час не надійшла жодна заявка (ймовірність ), один з n каналів звільнився (ймовірність
)
і жодна заявка з черги не покинула
систему не обслугованою (ймовірність
;в систему за час не надійшла жодна заявка (ймовірність ), жоден з n каналів не звільнився (ймовірність
)
і одна заявка покинула чергу не
дочекавшись обслуговування (ймовірність
)
;в систему за час надійшли l (l ≥ 1) заявки (ймовірність ), s каналів з n каналів звільнилися (ймовірність ) і
заявки покинули чергу без обслуговування
(ймовірність
).
Отже ймовірність дорівнює:
).
Аналогічно знаходимо, що .
Отже, однорідний ланцюг Маркова є процесом розмноження і загибелі. Розмічений граф станів для такого процесу має вигляд:
Стан Еn+m означає, що n заявок обслуговуються, а m знаходяться в черзі. Використовуючи даний граф та мнемонічне правило, запишемо систему диференціальних рівнянь для :
.
Припустимо, що
.
Умова нормування буде мати вигляд: .