Час обслуговування
Час обслуговування Т показує, скільки часу витрачено на обслуговування однієї заявки даним каналом. Очевидно, що Т є випадковою величиною. Будемо вважати, що вона має показниковий закон розподілу, при якому функція розподілу має вигляд:
,
(1.3)
де μ – параметр.
Як відомо математичне сподівання випадкової величини, що має показників закон розподілу, дорівнює:
.
Отже, величина
– середній час обслуговування однієї
заявки одним каналом, а величина μ
– середнє число заявок, яке може обслужити
один канал за одиницю часу.
Показниковий закон обраний невипадково. При показниковому розподілу часу обслуговування тривалість обслуговування, що залишалась, не залежить від того, скільки обслуговування вже тривало. Дійсно,
.
Отже,
,
а ця рівність означає, що
ймовірність того, що час обслуговування
буде меншим за
,
при умові, що обслуговування вже триває
більше ніж t,
дорівнює ймовірності того, що час
обслуговування буде меншим за h.
Показниковий закон розподілу гарно описує ті випадки, коли основна маса заявок обслуговується досить швидко, а затримки в обслуговуванні трапляються рідко. Це має місце в реальних СМО. Інколи час обслуговування краще описується іншими законами. Наприклад, законом розподілу Ерланга, щільність розподілу якого має вигляд:
.
Розподіл Ерланга представляє собою суму k незалежних випадкових величин, кожне з яких має показниковий закон розподілу з параметром μ. Математичне сподівання розподілу Ерланга дорівнює:
.
Всі типи СМО ми будемо розглядати при умові того, що час обслуговування має показниковий закон розподілу. Формули, отримані при цьому припущені, залишаються справедливими при довільному закону розподілу часу обслуговування, якщо математичне сподівання його скінченне і стале. Цей факт було доведено Б.А. Севастьяновим.
Ланцюг Маркова
Випадковий процес Х(t)
з дискретною множиною значень
називається ланцюгом
Маркова, якщо для
довільних моментів часу
виконується рівність:
.
(1.4)
Умовна ймовірність
називається перехідною
ймовірністю для
ланцюга Маркова.
Якщо умовно вважати
минулим,
теперішнім, а
майбутнім, то в рівності (1.4) втілюється
марковський принцип для ланцюга Маркова:
перехідна ймовірність
не зміниться від додаткового знання
значень процесу в минулі моменти
.
При розгляданні ланцюга
Маркова зручно користуватись поняттям
абстрактної фізичної системи, яка може
знаходитись в одному зі станів
.
Будемо казати, що система в момент часу
знаходиться в стані
,
якщо
.
Тоді перехідна ймовірність
– це умовна ймовірність того, що система
в момент часу
буде знаходитись в стані
,
якщо в момент часу
вона була в стані
.
Ланцюг Маркова називається
однорідним,
якщо перехідні ймовірності
залежать тільки від різниці моментів
:
.
Припустимо, що існують скінченні границі:
.
(1.5)
Числа
називають щільностями
ймовірності переходу системи із стану
в стан. Співвідношення (1.5) можуть бути
записані у вигляді:
.
При розгляді випадкових
процесів з дискретною множиною значень
і неперервним часом зручно уявляти
собі, що переходи системи із стану в
стан відбуваються під дією деяких
потоків подій; при цьому щільності
ймовірностей переходу системи із стану
в стан
отримують зміст інтенсивностей
відповідних потоків (як тільки відбувається
перша подія в потоці з інтенсивністю
,
система із стану
переходить в стан
).
Якщо всі ці потоки найпростіші, то
процес, що протікає в системі, буде
марковським.
Розглядаючи марковські випадкові процеси з дискретною множиною значень і неперервним часом, зручно користуватись графом станів, на якому проти кожної стрілки, що веде із стану в стан , проставлена інтенсивність , потоку подій, що переводить систему по даній стрілці. Такий граф станів називають розміченим.
Наряду з перехідними
ймовірностями
розглянемо ймовірності
того, що система в момент часу
буде в стані
.
Для знаходження цих ймовірностей
необхідно розв’язати систему
диференціальних рівнянь (рівнянь
Колмогорова), що має вигляд:
.
(1.6)
Рівняння (1.6) зручно складати користуючись розміченим графом станів системи та наступним мнемонічним правилом: похідна ймовірностей кожного стану дорівнює сумі добутків ймовірностей всіх станів, з яких ведуть стрілки в даний стан на інтенсивності відповідних потоків мінус добуток ймовірності даного стану на сумарну інтенсивність всіх потоків, що виводять систему з даного стану.
Якщо існують
і не залежать від початкового стану
системи, то
називаються фінальними
(граничними) ймовірностями.
Фінальну ймовірність можна тлумачити як середній відносний час знаходження системи в стані . Для того, щоб знайти фінальні ймовірності, треба розв’язати систему алгебраїчних рівнянь, яка утворюється із системи диференціальних рівнянь Колмогорова (1.6), якщо ліві частини покласти рівними нулю.
Процесом розмноження і загибелі називають випадковий процес, що задовольняє умови:
1) він є однорідним ланцюгом Маркова з неперервним часом і дискретною множиною значень;
2) за нескінченно малий проміжок часу h:
,
,
,
,
.
Розмічений граф станів для процесу розмноження і загибелі має вигляд:
Система диференціальних рівнянь Колмогорова для процесу розмноження і загибелі має вигляд:
Фінальні ймовірності станів системи для процесу розмноження і загибелі виражаються формулами:
,
,
…,
,
(1.7)
.
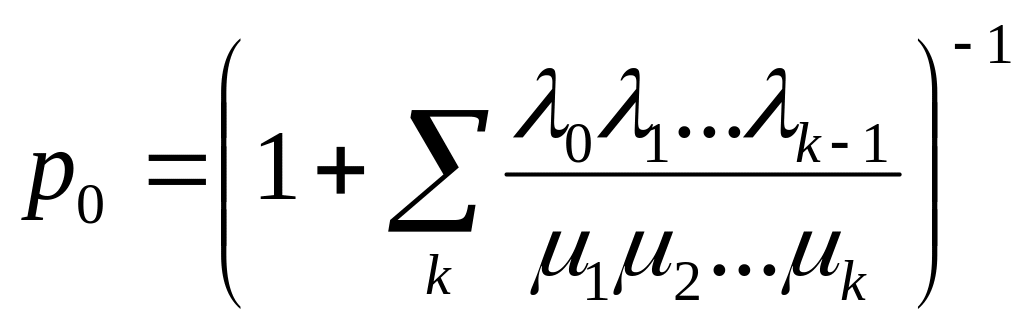(1.8)