V. Розв’язування типових задач

1. Потік відмов в роботі радіотехнічного пристрою найпростіший з параметром λ. Якщо пристрій відмовив, то несправність усувається. Час усунення несправності має показниковий закон розподілу з параметром μ. Знайдіть ймовірність того, що в момент t пристрій буде справний, якщо в початковий момент він також був справний.

Розв’язання. Пристрій при зроблених припущеннях має два стани:

Е₀ – пристрій справний;

Е₁ – пристрій ремонтується.

Ймовірності цих станів позначимо через і . Розмічений граф станів випадкового процесу, що описує роботу побудованої системи має вигляд:

Складемо систему диференціальних рівнянь Колмогорова:

.

Початкові умови: , . Замість другого рівняння розглянемо умову нормування . Тоді з першого рівняння маємо:

.

Звідси

.

Це лінійне диференціальне рівняння першого порядку з постійними коефіцієнтами. Його розв’язок має вигляд:

.

Покладемо і одержуємо:

.

Отже,

;

.

Ймовірність того, що в момент t пристрій буде справний дорівнює: .

При одержуємо стаціонарний режим роботи системи з ймовірностями:

, .

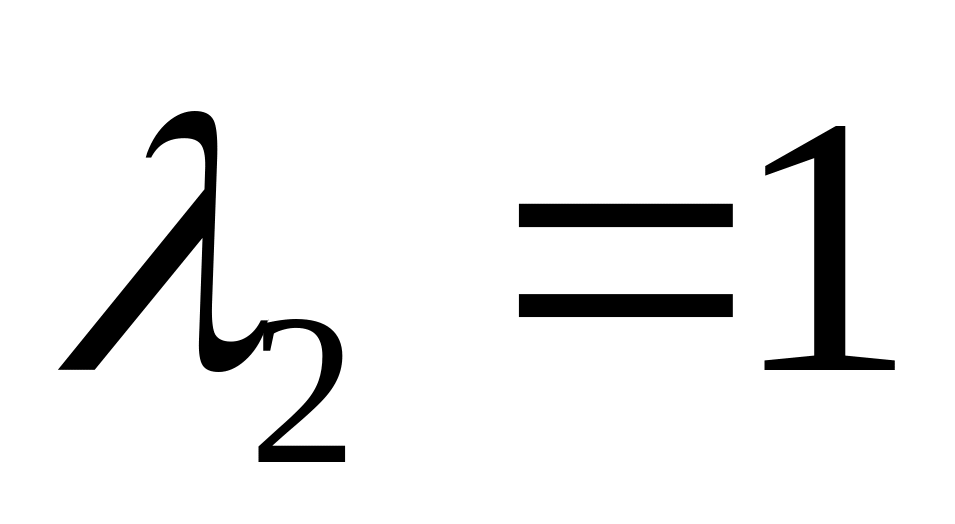2. Технічний пристрій складається з двох вузлів, кожний з яких у випадкові моменти часу може відмовити, після чого миттєво починається ремонт вузла, який триває випадковий час. Потік відмов кожного вузла є простішим з інтенсивністю для першого вузла і для другого. Час ремонту вузла має показниковий закон розподілу з параметром для першого вузла і для другого. Який відсоток часу обидва вузли працюють, тільки перший, тільки другий, обидва не працюють?

Розв’язання. Пристрій при зроблених припущеннях має чотири стани:

Е₀ – обидва вузли справні;

Е₁ – перший вузол ремонтується, другий справний;

Е₂ – другий вузол ремонтується, перший справний;

Е₄ – обидва вузли ремонтується.

Ймовірності цих станів позначимо через і , , . Розмічений граф станів випадкового процесу, що описує роботу побудованої системи має вигляд:

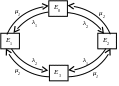
Складемо систему диференціальних рівнянь Колмогорова:

.

Оскільки число станів системи скінчене і з кожного стану можна перейти в кожний, то фінальні ймовірності існують. Вони є розв’язками алгебраїчної системи рівнянь:

.

Одне рівняння системи, наприклад останнє, можна опустити, а замість нього додати умову нормування: . Маємо:

.

Розв’язуємо цю систему і маємо: , , , . Отже, в стаціонарному режимі, 60% часу обидва вузли справні, 5% часу перший вузол ремонтується, а другий справний, 20% часу другий вузол ремонтується, а перший справний, 15% часу обидва вузла ремонтуються.

3. В деякій області діти народжуються з інтенсивністю одне народження кожні 10 хвилин. Час між народженнями має показниковий закон розподілу. Знайдіть:

а) середнє число народжень за годину;

б) ймовірність того, що за годину народиться 5 дітей;

в) ймовірність того, що за годину народиться більше 5 дітей.

Розв’язання. Кількість дітей , що народжуються в області за час τ, має Пуасонівський закон розподілу з інтенсивністю дітей за годину.

Використовуючи таблицю 1, знаходимо ймовірність того, що за годину народиться 5 дітей:

.

Використовуючи таблицю 2, знаходимо ймовірність того, що за добу народиться не менше 5 дітей:

.

4. Потік дзвінків на довідкову службу найпростіший з середнім дзвінки за одну хвилину. Тривалість телефонної розмови є випадковою величиною, що має показниковий закон розподілу з параметром . Знайдіть:

   1. необхідне число ліній для того, щоб ймовірність відмови не перевищувала 0,01;

б) середнє число зайнятих ліній.

Розв’язання. Дана СМО є з відмовами. Необхідне число ліній (каналів обслуговування) треба вибрати так, щоб

.

За формулою (2.6)

.

В даній задачі . Використовуючи таблиці 1 і 2 знаходимо, що при

,

що більше, ніж 0,01, а при

,

що менше, ніж 0,01. Тому – найменше число ліній, які треба для того, щоб .

Середнє число зайнятих ліній за формулою (2.7) дорівнює:

,

тобто в середньому одна з п’яти ліній буде весь час зайнята.

5. На вхід одноканальної СМО з відмовами поступає найпростіший потік заявок з інтенсивністю заявки за хвилину. Час обслуговування має показниковий закон розподілу. Середня тривалість обслуговування однієї заявки хвилини. Знайдіть:

а) фінальні ймовірності станів СМО;

б) абсолютну та відносну пропускну спроможність СМО.

Розв’язання. В даній задачі . За формулою (2.5) знаходимо:

,

.

Відносна пропускна спроможність СМО, тобто ймовірність обслуговування заявки, що поступила на СМО дорівнює:

.

Отже, в середньому 45,5% заявок, що надходять до СМО, будуть обслуговані.

Абсолютна пропускна спроможність СМО, тобто середнє число заявок, що обслуговує СМО за одиницю часу за формулою (2.7) дорівнює:

.

Отже, в середньому 0,182 заявки за хвилину будуть обслуговані.

6. Заправна станція має 5 бензоколонок. Відомо, що в середньому заправка однієї машини займає 4 хвилини. На станцію прибуває в середньому одна машина за хвилину. Знайдіть:

а) ймовірність очікування заправки;

б) середнє число машин в черзі на заправку;

в) середній час очікування заправки.

Розв’язання. Очевидно, що дану заправну станцію можна розглядати як СМО з очікуванням (обмежень на довжину черги або на час очікування немає) і з найпростішою дисципліною обслуговування. Число каналів обслуговування . Параметр вхідного потоку заявок . Середній час обслуговування однієї заявки , щільність завантаження

,

а завантаження СМО

.

Отже, необхідна умова усталеного режиму роботи СМО с очікуванням виконується.

а) Знайдемо ймовірність того, що всі п’ять бензоколонок зайняті за формулою (3.5), враховуючи, що шукається за формулою (3.4) і використовуючи таблиці 1 і 2:

.

Ймовірність очікування заправки шукаємо за формулою (3.6)

.

б) Середнє число машин в черзі на заправку знаходиться за формулою (3.7):

,

тобто в середньому 2 машини будуть стояти в черзі.

в) Середній час очікування заправки за формулою (3.13) дорівнює:

.

7. Залізнична каса з двома віконцями продає квитки в два напрямки. Інтенсивність пасажирів, що хочуть купити квитки, для обох напрямків однакова: (пасажирів за хвилину). На обслуговування пасажир витрачає в середньому 2 хвилини. Розглядаються два варіанти продажу квитків: перший – квитки продаються в двох віконцях на обидва напрямки зі спільною чергою; другий – в кожному віконцю продаються квитки на свій напрямок. Необхідно порівняти два варіанти продажу квитків.

Розв’язання. В обох варіантах маємо СМО з необмеженою чергою. В першому варіанті на СМО поступає потік заявок з інтенсивністю , число каналів обслуговування , щільність завантаження ; а завантаження СМО

.

За формулою (3.5) знайдемо ймовірність того, що обидна канали обслуговування зайняті , враховуючи, що шукається за формулою (3.4):

.

Ймовірність очікування обслуговування за формулою (3.6) дорівнює:

.

Отже, середній час очікування обслуговування за формулою (3.13) дорівнює:

.

Очевидно, що середній час, який витратить пасажир для купівлі квитка, дорівнює сумі середнього часу знаходження в черзі та середнього часу обслуговування:

.

В другому варіанті маємо дві одноканальні СМО, на кожну з яких поступає потік заявок з інтенсивністю . Щільність завантаження ; а завантаження СМО

.

Ймовірність зайнятості кожного каналу обслуговування:

.

Ймовірність очікування обслуговування за формулою (3.6) дорівнює:

.

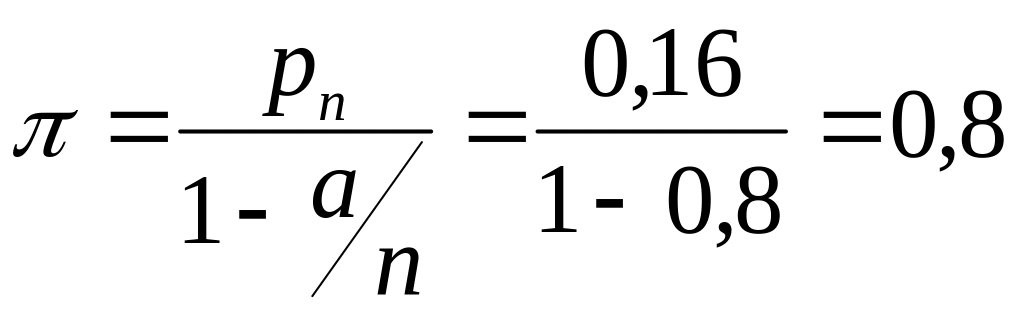Отже, середній час очікування обслуговування за формулою (3.13) дорівнює:

.

Середній час, який витратить пасажир для купівлі квитка, дорівнює:

.

Отже, в другому варіанті середній час, який пасажир витрачає на купівлю квитка, більший ніж в першому. Це цілком зрозуміло, бо в другому варіанті касири не можуть підміняти один одного, тобто обслуговувати пасажирів, що купують квиток в іншому напрямку, коли немає пасажирів, що купують квиток в даному напрямку.

8. На станцію поточного ремонту машин поступає найпростіший потік несправних машин з інтенсивністю 2 машини за добу. Станція має три однакові лінії ремонту. Місць для несправних машин, що очікують ремонту, не більше шести. Час, який витрачається на ремонт залежить від багатьох факторів, а тому є випадковим. Статистичні дані свідчать, що він має показниковий закон розподілу з середнім значенням 3 доби. Знайдіть:

а) ймовірність того, що несправна машина не буде прийнята на ремонт;

б) ймовірність очікування ремонту;

в) середнє число машин, що чекають на ремонт;

г) середній час очікування ремонту.

Розв’язання. Очевидно, що дану ремонтну станцію можна розглядати як СМО змішаного типу з обмеженням на довжину черги і з найпростішою дисципліною обслуговування. Число каналів , обмеження на довжину черги . Параметр вхідного потоку заявок . Середній час обслуговування однієї заявки , щільність завантаження

,

а завантаження СМО

.

За формулою (4.2) знайдемо ймовірність того, що в СМО знаходиться рівно три заявки, тобто всі лінії зайняті ремонтом, а в черзі машин немає:

.

а) ймовірність того, що несправна машина не буде прийнята на ремонт за формулою (4.4) дорівнює:

.

б) ймовірність очікування ремонту шукаємо за формулою (4.5):

.

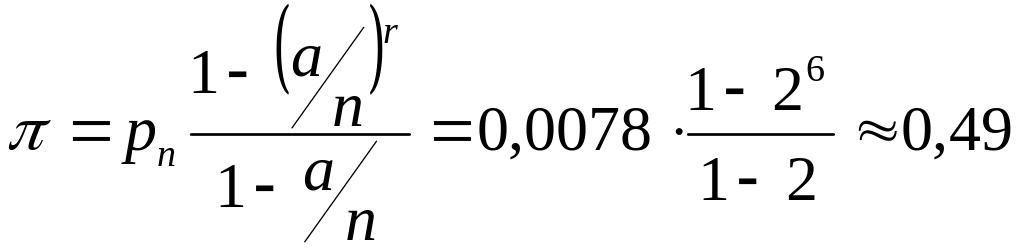в) середнє число машин, що чекають на ремонт шукаємо за формулою (4.6):

.

г) середній час очікування ремонту шукаємо за формулою (4.9):

.

9. Продуктовий магазин має дві каси для обслуговування клієнтів. Одна з них працює весь час. Якщо в черзі знаходиться більше двох покупців, то відкривається і друга каса. Покупці надходять до кас у відповідності до закону Пуасона з інтенсивністю 8 осіб за годину. Час обслуговування одного клієнта в касі має показниковий закон розподілу із середнім значенням 12 хвилин. Знайдіть ймовірність того, що буде працювати тільки одна каса.

Розв’язання. Робота СМО описується випадковим процесом – кількістю покупців в магазині в момент часу t. Частина їх обслуговується, інші очікують обслуговування в черзі. Можливими значеннями цього процесу є числа 0, 1, 2, …, n, ….

Якщо , то працює одна каса, якщо , то працюють дві каси.

Випадковий процес є процесом розмноження і загибелі. Розмічений граф станів для процесу має вигляд:

За умовою задачі , . Фінальні ймовірності станів системи для процесу розмноження і загибелі знаходимо за формулами (1.7) і (1.8):

; ; ; ,

,

.

Одна каса буде працювати, якщо в системі знаходиться не більше трьох покупців, тобто

.

10. Задля збільшення дальності безпосадкового польоту провадиться дозаправка літаків в повітрі. В заданому районі постійно чергують чотири літаки-заправники. В середньому дозаправка триває 10 хвилин. Очікувати заправки літак може в середньому не більше 20 хвилин. В середньому в район дозаправки прилітають 24 літаки на годину. Знайдіть:

а) середнє число літаків, що очікують дозаправки;

б) ймовірність отримання дозаправки.

Розв’язання. Очевидно, що дану дозаправку літаків можна розглядати як СМО змішаного типу з обмеженням часу очікування обслуговування. Число каналів обслуговування . Параметр вхідного потоку заявок (середнє число літаків, що прилітають на дозаправку за хвилину). Середній час обслуговування однієї заявки , середній час очікування дозаправки . Отже,

; ; .

а) За формулою (4.13) середнє число літаків, що чекають дозаправки, дорівнює:

.

б) Ймовірність дозаправки за формулою (4.15), дорівнює:

.

60