VI. Смо змішаного типу

1. Марковський процес, що описує смо змішаного типу з обмеженням довжини черги

СМО складається з n каналів обслуговування. Починаючи з моменту часу на вхід СМО поступає найпростіший потік заявок з інтенсивністю λ. Якщо є вільні канали, то заявка починає обслуговуватись одним каналом, якщо всі канали зайняті, то заявка стає в чергу. В черзі може знаходитись не більше ніж r заявок, дисципліна обслуговування простіша. Час обслуговування Т має показниковий закон розподілу з параметром μ, причому будемо вважати, що час обслуговування даної заявки не залежить від часу обслуговування інших заявок та від інших заявок, що поступають.

Робота СМО описується випадковим процесом – кількістю заявок в системі в момент часу t. Частина цих заявок може обслуговуватись, інші очікують обслуговування в черзі. Можливими значеннями цього процесу є числа 0, 1, 2, … , n, n + 1, ... , n + r. Так само, як в попередніх розділах, неважко переконатись в тому, що випадковий процес є однорідним ланцюгом Маркова з дискретною множиною значень і неперервним часом.

Якщо , тобто в момент часу t в системі знаходиться k заявок, то будемо вважати, що система знаходиться в стані . Позначимо через ймовірність того, що в момент часу t система знаходиться в стані , тобто

.

Розмічений граф станів для процесу має вигляд:

Стан Е_n+m означає, що n заявок обслуговуються, а m знаходяться в черзі. Використовуючи даний граф та мнемонічне правило, запишемо систему диференціальних рівнянь для :

.

Припустимо, що

.

Умова нормування буде мати вигляд: .

2. Усталений режим роботи смо змішаного типу з обмеженням на довжину черги

Аналогічно до СМО з відмовами та чергою, можна довести, що СМО з очікуванням при великих t працює в усталеному режимі, тобто існують фінальні ймовірності:

,

а .

Переходячи до границі при в системі Ерланга, отримуємо алгебраїчну систему:

. (4.1)

Умова нормування приймає вигляд: .

Розв’язуючи дану систему аналогічно до системи (3.1), отримуємо:

(4.2)

де – щільність завантаження системи.

Ймовірність р₀ (ймовірність того, що всі канали вільні) знаходимо використовуючи умову нормування:

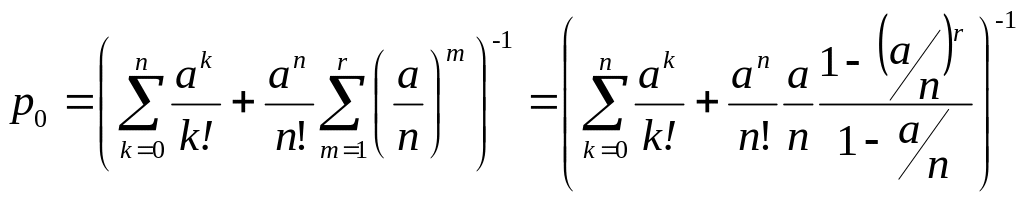, (4.3)

якщо .

Ймовірність відмови, очевидно, дорівнює:

, (4.4)

а ймовірність обслуговування:

.

Знайдемо ймовірність очікування обслуговування, тобто ймовірність зайнятості всіх n каналів:

. (4.5)

Середню довжину черги шукаємо як математичне сподівання числа заявок, що знаходяться в черзі:

.

Для знаходження цієї суми зробимо наступні перетворення:

.

Отже,

. (4.6)

Середнє число зайнятих каналів:

. (4.7)

Середнє число заявок в СМО дорівнює сумі середнього числа заявок в черзі та середнього числа заявок, що обслуговуються (середнє число зайнятих каналів):

. (4.8)

3. Час знаходження заявки в черзі

Нехай СМО працює в усталеному режимі. Функція розподілу випадкової величини Y (часу очікування заявки початку обслуговування) знаходиться аналогічно випадку СМО з очікуванням.

Наводячи практично дослівно міркування наведені в попередньому розділі, маємо:

.

Міняємо порядок підсумовування і одержуємо:

.

Отже,

.

Очевидно, що при . Отже функція розподілу часу знаходження заявки в черзі має вигляд:

.

Середній час очікування обслуговування дорівнює математичному сподіванню часу знаходження заявки в черзі. Його можна знайти простіше, використовуючи формулу Літтла (1.8):

(4.9)

За першою формулою Литтла (1.9) можна знайти середній час перебування заявки в системі:

,

( шукається за формулою (4.8)).