Qr факторизация.
Функция qr выполняет QR разложение матрицы. Эта операция полезна как для квадратных, так и для прямоугольных матриц. Исходная матрица представляется в виде произведения действительной ортонормальной или комплексной унитарной матрицы Q и верхней треугольной матрицы R. Функция используется в следующих формах:
[Q, R] = qr(A) вычисляет верхнюю треугольную матрицу R того же размера, что и A, и унитарную матрицу Q, так что A = Q*R;
[Q, R, E] = qr(A) вычисляет матрицу перестановок E, верхнюю треугольную матрицу R c убывающими по модулю диагональными элементами и унитарную матрицу Q, так что A*E = Q*R;
[Q, R] = qr(A,0) и [Q, R, E] = qr(A, 0) вычисляют экономное разложение, в котором E – вектор перестановок такой, что Q*R = A(:, E). Вектор E выбирается так, чтобы диагональные элементы матрицы R убывали по модулю;
X = qr(A) возвращает результат из пакета LAPACK так, что R есть triu(X) – верхняя треугольная часть матрицы X. Матрица R позволяет избежать потери точности при вычислении A'*A с помощью разложения Холецкого: A'*A = R'*R .
В качестве примера рассмотрим QR разложение прямоугольной матрицы C:
C = fix(10*rand(3, 2))
C =
6 8
9 6
1
[Q, R] = qr(C)
Q =
-0.4460 0.7450 0.4961
-0.6690 0.0908 -0.7377
-0.5946 -0.6609 0.4579
R =
-13.4536 -8.1762
0 5.8437
0
Во многих случаях последние m-n столбцы матрицы Q можно отбросить, так как они умножаются на последние нулевые строки матрицы R. Используя экономный формат функции разложения, получим:
[Q, R] = qr(C, 0)
Q =
-0.4460 0.7450
-0.6690 0.0908
-0.5946 -0.6609
R =
-13.4536 -8.1762
5.8437
Решение системы Cx = u с факторизованной матрицей находится в два этапа:
y = Q'*u;
x = R\y
x =
0.3590
-0.0544
Поскольку матрица системы является переопределенной, то найденное решение является наилучшим среднеквадратичным приближением. Отметим, что оператор x = C\u даст такой же результат.
Матричная экспонента.
Матричная экспонента expm(X) возводит число e в матричную степень X. Рассмотрим в качестве примера задачу Коши для системы обыкновенных дифференциальных уравнений первого порядка с постоянными коэффициентами:
dx/dt=Ax, x(0)=u,
здесь x = x(t) – векторная функция, A – матрица коэффициентов, u – вектор начальных условий. Решение задачи можно выразить через матричную экспоненту x(t)=etAx(0).
Положим:
A=[0 -6 -1; 6 2 -16; -5 20 -10];
u=[1; 1; 1];
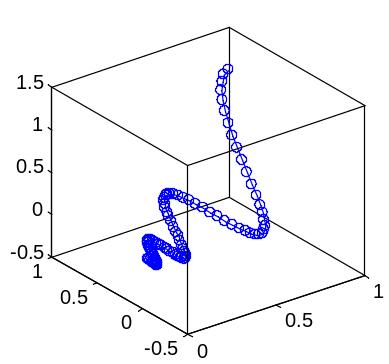
Определим решение системы дифференциальных уравнений в узлах равномерной сетки с шагом 0.1 на отрезке [0, 1] и построим трехмерный график фазовой траектории:
X = [];
for t = 0:.01:1
X = [X expm(t*A)*u];
end
plot3(X(1,:), X(2,:), X(3,:),'-o')
box on
Собственные значения и собственные вектора.
Скаляр и вектор v называются собственным значением и собственным вектором матрицы A, если выполняется соотношение: Av=v. Пусть – диагональная матрица, у которой на диагонали стоят собственные значения матрицы A, а V – матрица, столбцами которой являются собственные вектора матрицы A. Тогда справедливо соотношение:
AV = V. Если V несингулярная матрица, то матрицу A можно представить в виде разложения: A = VV-1. Возьмем матрицу A из предыдущего примера:
A =
0 -6 -1
6 2 -16
-5 20 -10
Тогда функция eig(A) возвращает вектор собственных значений матрицы A:
lambda = eig(A)
lambda =
-3.0710
-2.4645 +17.6008i
-2.4645 -17.6008i
Так как действительная часть собственных значений является отрицательной, то et стремится к нулю с ростом t. Ненулевая мнимая часть двух собственных значений, , является осциллирующей, sin(t), компонентой решения дифференциального уравнения.
Для вычисления собственных значений и собственных векторов матрицы A используется формат команды eig с двумя выходными параметрами:
[V, D] = eig(A)
V =
-0.8326 0.2003 - 0.1394i 0.2003 + 0.1394i
-0.3553 -0.2110 - 0.6447i -0.2110 + 0.6447i
-0.4248 -0.6930 -0.6930
D =
-3.0710 0 0
0 -2.4645 +17.6008i 0
0 0 -2.4645 -17.6008i
Собственные векторы хранятся в столбцах матрицы V, а собственные значения – в диагональных элементах матрицы D. Собственные векторы масштабированы так, чтобы евклидова норма каждого вектора равнялась единице.