Численное интегрирование.

Численное интегрирование заключается в приближенном вычислении определенного интеграла с помощью одной из квадратурных формул. Рассмотрим применение функции quad, которая выполняет интегрирование по методу низкого порядка, используя рекурсивное правило Симпсона.

Найдем значение определенного интеграла для функции f(x)=x³ на отрезке [0, 1] :

quad('x.^3', 0, 1, 1.e-8)

ans =

0.2500

Перечислим входные параметры. Первый аргумент описывает подынтегральную функцию и может быть строковой константой, указателем функции или операторной функцией. Второй и третий параметры задают пределы численного интегрирования. Последний параметр задает относительную погрешность метода.

Для вычисления двойного интеграла можно использовать функцию dblquad:

q = dblquad(fun, xmin, xmax, ymin, ymax, tol)

здесь fun – подынтегральная функция, tol – относительная погрешность, а остальные параметры задают пределы интегрирования.

Пример:

Q = dblquad(inline('y*sin(x)+x*cos(y)'), pi, 2*pi, 0, pi)

Q =

-9.8696

Представление полиномов в среде matlab.

В системе MATLAB полином представляется с помощью вектора-строки, содержащего упорядоченные по убыванию коэффициенты полинома. Например, чтобы представить многочлен p(x)=x³-2x-5, следует создать вектор:

p = [1 0 -2 -5];

Умножение и деление многочленов.

Для реализации умножения и деления многочленов следует использовать функции conv и deconv. Рассмотрим многочлены a(s)=s²+2s+3 и b(s)=4s²+5s+6. Вычислим их произведение:

a = [1 2 3]; b = [4 5 6];

c = conv(a, b)

c =

4 13 28 27 18

Разделим многочлен c на a:

[q, r] = deconv(c, a)

q =

4 5 6

r =

0 0 0 0 0

Вектор r представляет собой остаток.

Вычисление производной от многочлена.

Для определения производной от многочлена используется функция polyder. Вычислим производную от многочлена p:

p = [1 0 -2 -5];

q = polyder(p)

q =

3 0 -2

Функция polyder позволяет находить производную от произведения двух многочленов и от их частного. Для примера, построим два многочлена a и b.

a = [1 3 5]; b = [2 4 6];

Вычислим производную от произведения a*b, используя вызов функции с одним выходным параметром:

c = polyder(a, b)

c =

8 30 56 38

Для вычисления производной от частного a/b, следует использовать вызов функции с двумя выходными параметрами:

[q, d] = polyder(a, b)

q =

-2 -8 -2

d =

4 16 40 48 36

где q/d является результатом операции.

Вычисление значения многочлена.

Для вычисления значения многочлена следует использовать функцию polyvalm:

p = [1 0 -2 -5];

polyval(p, 5)

ans =

110

Функция polyvalm позволяет также вычислять матричный многочлен. Вычислим значение многочлена p(X)=X³-2X-5I от квадратной матрицы X :

X = [2 4 5; -1 0 3; 7 1 5];

Y = polyvalm(p, X)

Y =

377 179 439

111 81 136

490 253 639

Нахождение корней многочлена.

Корни многочлена можно найти с помощью функции roots:

r = roots(p)

r =

2.0946

-1.0473 + 1.1359i

-1.0473 - 1.1359i

Здесь p – вектор из предыдущего примера, r – вектор, компонентами которого являются корни многочлена.

Построение многочлена по его корням.

Функция poly возвращает коэффициенты многочлена, если корни его известны:

p2 = poly(r)

p2 =

1.0000 0 -2.0000 -5.0000

Построение характеристического многочлена.

Если в качестве аргумента использовать матрицу, то функция poly возвращает коэффициенты характеристического многочлена:

A=[1 2 3; 4 5 6; 7 8 0]

A=

1 2 3

4 5 6

7 8 0

p = poly(A)

p =

1. -6.0000 -72.0000 -27.0000

Минимизация функций.

Для нахождения минимума функции одной переменной на заданном интервале следует использовать функцию fminbnd. Найдем на интервале [0.2, 1] минимум функции

f = inline('1./((x-0.3).^2 + 0.01) + 1./((x-0.9).^2 + 0.04)-6');

x = fminbnd(f, 0.2, 1)

x =

0.6370

fplot(f,[0.2 1]); grid on;

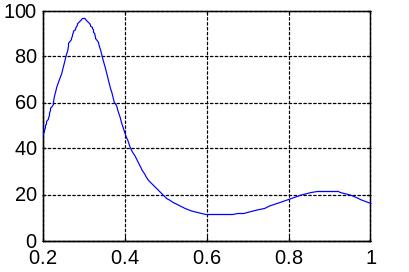
Функция fplot используется для вывода графика операторной функции f на заданном интервале [0.2, 1].

Для минимизации функций нескольких переменных можно использовать функцию fminsearch. Поиск минимума основан на симплекс-методе Нелдера – Мида, который сводится к построению симплекса в n-мерном пространстве, заданного n+1 вершиной. В двумерном пространстве симплекс является треугольником, а в трехмерном – пирамидой. На каждом итерационном шаге значение функции в новой точке (приближенном решении) сравнивается со значениями функции в вершинах симплекса. В результате новая точка заменяет ближайшую вершину симплекса. Итерации повторяются до тех пор, пока размеры симплекса не станут меньше заданной погрешности метода.

В качестве примера рассмотрим поиск минимума тестовой функции Розенброка:

Минимальное значение этой функции равно нулю и достигается в точке [1, 1].

f = inline('100*(x(2)-x(1)^2)^2+(1-x(1))^2;');

[x, fval] = fminsearch(f,[-1.2, 1])

x =

1.0000 1.0000

fval =

8.1777e-010

Первый входной параметр функции fminsearch описывает функцию одной или нескольких переменных, а второй параметр задает нулевое приближение и может быть скаляром, вектором или матрицей. Приведем текст программы, которая строит сетчатую поверхность функции Розенброка и отмечает точками на графике каждый итерационный шаг:

x=-2:.25:2; y=-1:.25:3;

[xx, yy]=meshgrid(x, y);

zz=100*(yy-xx.^2).^2+(1-xx).^2;

mesh(x, y, zz, 'FaceColor', 'non', 'EdgeColor', 'k');

axis off; view(13,32);

hold on;

plot3(-1.9, 2, 267.62,'ko','MarkerSize', 15,

'LineWidth', 2, 'EraseMode', 'none');

text(-1.9, 2.2, 267.62,' Begin', 'Color',[0 0 0], 'EraseMode','none');

plot3(1,1,0,'ko', 'MarkerSize',15, 'LineWidth',2, 'EraseMode','none');

text(0.8, 1.4, 0,' End', 'Color',[0 0 0], 'EraseMode','none');

x=[-1.9 2]; % Начальное приближение

f='[100*(x(2)-x(1)^2)^2+(1-x(1))^2; minfn(x)]';

[x, fval, exitflag, output] = fminsearch(f, x);

function out=minfn(currPos)

x1=currPos(1); y1=currPos(2);

z1=100*(y1-x1.^2).^2+(1-x1).^2;

plot3(x1,y1,z1,'r.', 'EraseMode','none', 'MarkerSize',25);

out = [];

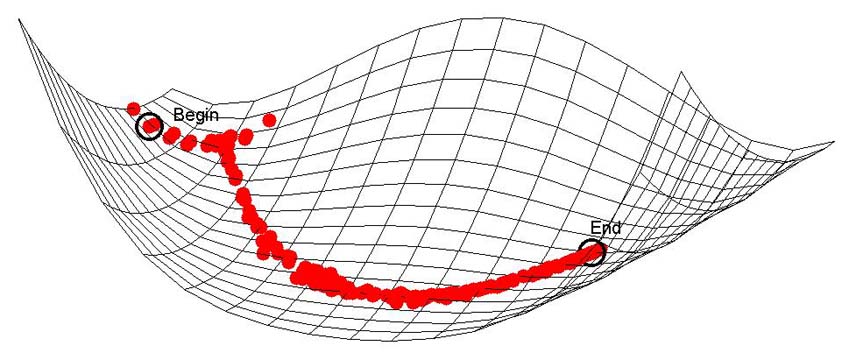
Метки Begin и End обозначают начальное и конечное приближение. Функции fminbnd и fminsearch входят в состав пакета Optimization Toolbox, который служит для решения оптимизационных задач и систем нелинейных уравнений.