1.16.2. Преобразование Фурье
Для получения искомого преобразования перепишем полученное выражение интеграла Фурье в следующем виде:
. (1.16.2.1)
Формула (1.16.5) получена введением отрицательных частот. Они не имеют физического смысла, однако позволяют сделать запись в более симметричной форме. Прибавим к данной функции мнимый ноль, который будет задан выражением
.
Воспользуемся формулой Эйлера для записи функции в показательном виде:
.
(1.16.2.2)
Отдельно выделим внутренний интеграл и произведем в нем замену τ на t, что всегда возможно для определенных интегралов:
(1.16.2.3)
Полученный интеграл представляет собой спектральную плотность функции f(t) и носит название прямого преобразования Фурье.
Так как функция комплексная S(jω) = S(ω)ejψ(ω) , то
S(ω) – амплитудно-частотная характеристика (АЧХ);
Ψ(ω) – фазо- частотная характеристика (ФЧХ).
Эти характеристики показывают закон распределения амплитуд и фаз по текущим частотам.
Если функция f(t) задана в интервале времени от 0 до t, то
.
Полученную комплексную функцию S(jω) подставим в исходный интеграл Фурье:
,
(1.16.2.4)
который называется обратным преобразованием Фурье.
Сравнение прямого преобразования Фурье и интеграла Лапласа показывает их совпадение при определенном условии.
Интеграл Лапласа:
Интеграл Фурье:
S(jω) = F(p), (p = jω).
Использовать преобразование Фурье можно в расчетах переходных процессов. Полученное равенство показывает, что преобразование Лапласа является более мощным, чем преобразование Фурье, p – может быть любым (вещественным, комплексным, мнимым), в то время как jω – чисто мнимое число.
Из сказанного следует, что когда для функции найдено лапласово преобразование, то для получения частотного спектра достаточно р заменить на jω в этом выражении, и выделить его АЧХ и ФЧХ.
1.16.3. Законы Ома и Кирхгофа для частотных спектров
Они полностью повторяют по форме записи соответствующих законов, которые были получены при рассмотрении операторного метода с той разницей, что оператор р заменяется на jω, поэтому ограничимся лишь финальным выражением:
.
(1.16.3)
Выражение в знаменателе представляет собой сопротивление цепи как функцию частоты, но ω при этом не является фиксированным числом.
Законы Кирхгофа:
,
1.16.4. Пример расчета спектральной плотности сигнала
Пусть на вход некоторого двухполюсника подается единичный импульс напряжения длиной t1:
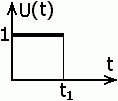
Рис.1.16.4.1. Единичный импульс напряжения
Определим частотный спектр этого импульса. Так как площадь импульса конечна, то преобразование может быть получено в следующем виде
,
Из полученного выражения для спектральной плотности выделим и построим АЧХ и ФЧХ:
.
На рис 1.16.4.2 представлена АЧХ заданной функции.
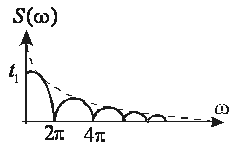
Рис.1.16.4.2. Амплитудно-частотная характеристика
единичного импульса напряжения
Аналогичного рода рассуждения позволяют построить ФЧХ функции, представленную на рис 1.16.4.3.
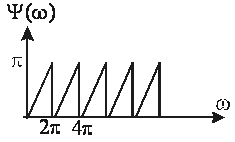
Рис.1.16.4.3. Фазо-частотная характеристика
единичного импульса напряжения