4.13. Потери на гистерезис

Периодическое перемагничивание ферромагнитного сердечника сопряжено с потерями энергии на гистерезис. Мощность этой составляющей является функцией целого ряда факторов. На основании проведенных исследований получена экспериментальная зависимость:

, (4.13)

где

- коэффициент, зависящий от марки стали;

f - частота переменного тока;

B_m - амплитуда магнитной индукции;

n = 1.6 при 0.1<B_m<1.0 Тл;

n = 2 при B_m>1.0 Тл;

G – масса магнитопровода.

4.14. Вихревые токи

Вихревые токи возникают вследствие того, что магнитопровод является проводящим и индуктируемая основным магнитным потоком ЭДС вызывает в сердечнике токи. Мощность, расходуемая в сердечнике из-за вихревых токов, определяется по формуле

, (4.14)

где σ_в.т.. – конструктивная постоянная.

Для уменьшения потерь от вихревых токов магнитопровод набирают из листов стали, изолированных друг от друга лаком. Так как потери P_в.т. зависят от частоты, то с ее увеличением толщина листов уменьшается. При f=50 Гц толщина листов составляет 0,35-0,5мм, а при f=400 Гц – 0,1- 0,35мм.

На частотах порядка десятков мегагерц магнитопровод изготовляют из феррита, который представляет собой спеченную массу ферромагнитных частиц и диэлектрика.

4.15. Влияние намагничивания на форму кривой тока и напряжения

Ранее было установлено, что синусоидальное напряжение, приложенное к катушке, вызывает появление синусоидального магнитного потока. Определим форму тока в катушке, считая, что магнитопровод изготовлен из магнитомягкого материала, что позволит пренебречь потерями в стали. Кроме того, примем сопротивление провода катушки равным нулю: (R_к = 0) и пренебрежем потоком рассеяния (Ф_s = 0). Для решения этой задачи воспользуемся графоаналитическим методом, который был рассмотрен ранее.

На рис 4.15.1 показан графический метод расчета тока катушки при синусоидальном напряжении источника. Из двух зависимостей i(Ф) и Ф(t) исключаем Ф и получаем зависимость i(t).

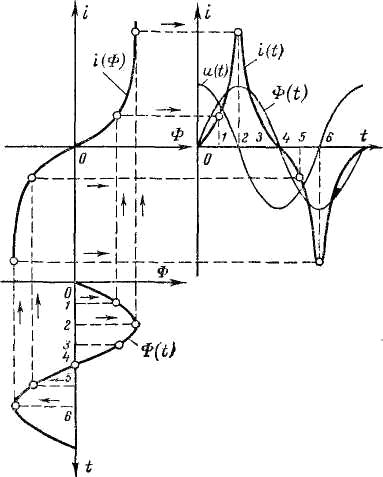
Рис.4.15.1. Графический расчет тока

по заданным зависимостям i(Ф) и Ф(t)

Форма тока получилась несинусоидальной, что указывает на искажение тока в нелинейных цепях, и это обстоятельство усложняет расчет. Кроме того, реальный магнитопровод имеет потери в стали, и в общем случае шириной петли гистерезиса пренебречь нельзя, т.к. ее ширина пропорциональна потерям на перемагничивание железа.

На рис. 4.15.2 построена зависимость i(t) с учетом петли гистерезиса. Построение зависимости i(t) производят аналогично предыдущему пункту, но здесь появляется угол δ, соответствующий ненулевому значению тока при нулевом значении магнитного потока, что свидетельствует о несовпадении фазы тока и магнитного потока. Угол δ, показывающий опережение тока относительно магнитного потока, называется углом магнитного запаздывания. Величина этого угла невелика (3-5⁰), но учет его приводит к необходимости учета потерь на нагрев сердечника. Рассмотрим один важный момент, который необходимо учитывать при практических расчетах таких цепей. Несинусоидальный ток, обусловленный нелинейностью катушки, будем рассматривать как синусоидальный ток, который по тепловому действию эквивалентен реальному несинусоидальному току. Такое возможно, если тепловое действие реального несинусоидального тока и эквивалентного синусоидального тока одинаково. Введение эквивалентных синусоид является чрезвычайно важным, поскольку позволяет использовать комплексный метод расчета и построение векторных диаграмм для действующих значений токов и напряжений.

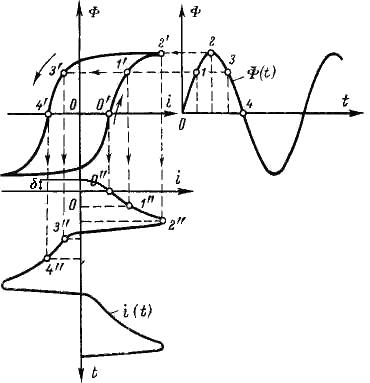
Рис.4.15.2. Графический расчет тока по заданным зависимостям i(Ф) и Ф(t) при учете петли гистерезиса