Классический метод расчета переходных процессов.
Классический метод расчета переходных процессов оси заключается в непосредственном решении системы интегро-дифференциальных уравнений, которыми описывается схема после коммутации.
1.2. Законы коммутации.
Первый закон коммутации.
Ток и потокосцепление в индуктивности не могут измениться скачком, т.е.
iL(-0)= iL(+0);
ψ(-0)=ψ(+0). (1.2.1)
При скачкообразном изменении потокосцепления или тока ток и потокосцепление в индуктивности не могут измениться скачком.
(1.2.2)
т. е нарушается второй закон Кирхгофа, т.к. падение напряжения на каком-либо участке не может принимать бесконечно большое значение.
Второй закон коммутации. Заряд и напряжение не могут измениться скачком
q(-0)=q(+0);
uc(-0)= uc(+0). (1.2.3)
В противном случае ток принимает бесконечно большое значение:
(1.2.4)
Перечисленные в законах коммутации величины носят название независимых начальных условий. Все остальные токи и напряжения носят название зависимых: iC(0); uL(0); iR(0); uR(0). Начальные условия могут быть нулевые и не нулевые.
Независимые начальные условия характеризуют энергию, запасенную в соответствующих элементах к моменту коммутации. Расчет цепей в переходных режимах будем вести, используя законы Кирхгофа.
Пусть задана цепь с элементами R, L, C (рис 1.1)
Рис 2.1. Схема коммутации
Составим дифференциальное уравнение цепи после коммутации относительно тока:
.
(1.2.5)
Полученное дифференциальное уравнение является неоднородным дифференциальным уравнением второго порядка. Решением данного уравнения является сумма двух решений, частного решения неоднородного уравнения и общего решения однородного. Частное решение называется принуждённой составляющей тока (напряжения). Это величина тока (напряжения), которая изменяется с той же частотой, что и действующая в схеме ЭДС. Будем обозначать их uпр, iпр.
Аналогичны решения однородного дифференциального уравнения (без источника ЭДС):
uR = uRсв;
uL = uLсв;
uC = uCсв.
Полное решение определяем по принципу наложения:
i= iпр + iсв,
т.е. все величины в цепи меняются по одному закону. В зависимости от порядка решаемого дифференциального уравнения выделяют цепи первого, второго и высшего порядка, а сам порядок дифференциального уравнения определяется количеством накопителей энергии.
1.3. Короткое замыкание цепи r-l
Пусть произошло короткое замыкание в катушке в схеме по рис. 1.3.1.:
Рис.1.3.1. Схема цепи
1.До коммутации:
2.Составим дифференциальное уравнение исходной цепи после коммутации:
,
где А – постоянная интегрирования, р – корень характеристического уравнения цепи после коммутации.
Вторым способом составления характеристического уравнения является способ, при котором в комплексной форме составляется входное сопротивление цепи относительно источника, оператор jω заменяется на p. Полученное выражение приравнивается к нулю. Такой способ удобнее применять в случае, когда переходный процесс происходит в сложной разветвленной цепи:
Определим постоянную A, используя независимое начальное условие. Данное уравнение справедливо для любого момента времени, в том числе для t = 0:
.
Проверка:
Для оценки
длительности переходного процесса
вводят понятие постоянной времени
.
За время t
= τ
величина свободного тока или напряжения
изменится в e
раз. Если с момента коммутации пройдет
время, равное 3τ,
то значение тока в переходном процессе
достигает 95% своего установившегося
значения, при t
= 5τ
- 99%.
Используя полученное
выражение для тока, получим функции
и
:
;
Проверка:
Построим графики полученных функций в переходном процессе (рис. 1.3.2.):
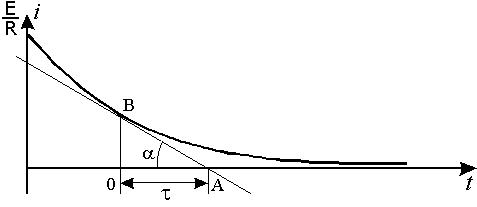
Рис.1.3.2. Графики зависимости i(t), uR(t), uL(t) в переходном процессе
Постоянная
времени может быть определена графически
следующим образом: определим производную
тока
и найдем отношение:
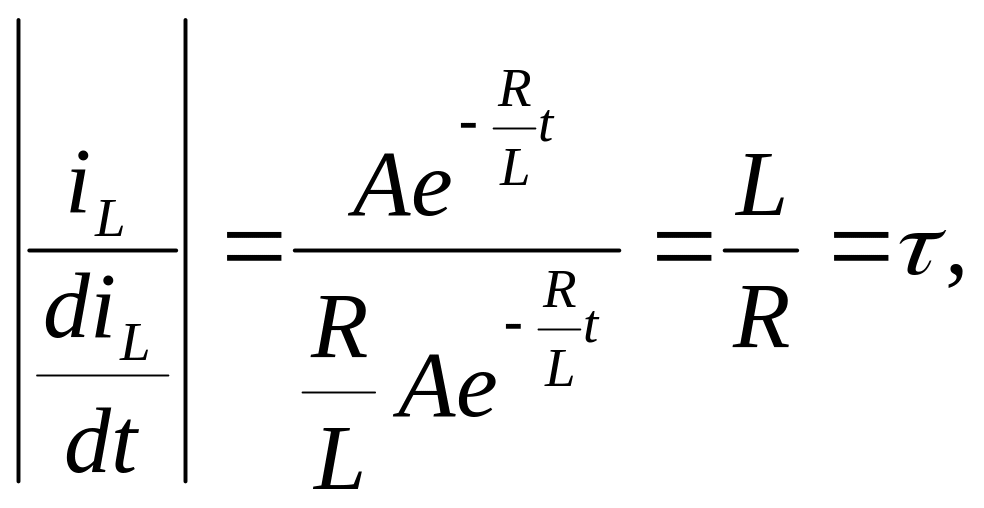
где
(рис 1.3.2.),
,
тогда величина подкасательной OA
.
Для определения численного значения необходимо отрезок OA умножить на масштаб mt.
Определим энергию, выделяющуюся в виде тепла на активном сопротивлении:
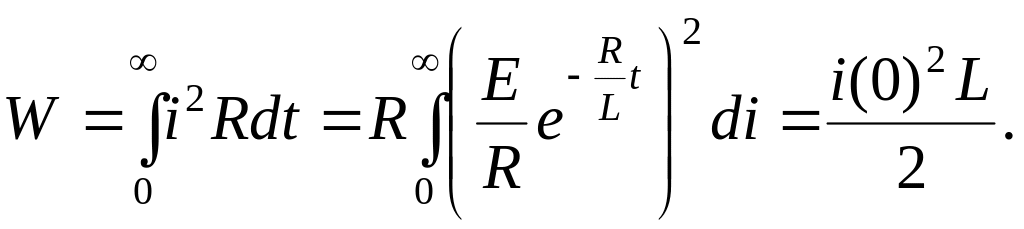
Полученный результат представляет энергию, запасенную индуктивностью к моменту коммутации.