
- •Часть 2
- •Переходные процессы в линейных электрических цепях
- •Классический метод расчета переходных процессов.
- •1.2. Законы коммутации.
- •1.3. Короткое замыкание цепи r-l
- •1.4. Включение r, l на постоянное напряжение
- •1.5. Включение цепи r-l к источнику синусоидального напряжения
- •1.6. Общая методика расчета переходных процессов
- •1.7. Операторный метод расчета переходных процессов
- •1.8. Закон Ома в операторной форме
- •1.9. Законы Кирхгофа в операторной форме
- •1.10. Формула разложения.
- •1.11. Методика расчета цепи операторным методом
- •1.12. Общая методика расчета цепи операторным методом
- •1.13. Переходный процесс в индуктивно связанных катушках
- •1.14. Интеграл Дюамеля
- •1.15. Пример расчета переходного процесса с помощью интеграла Дюамеля
- •1.16. Частотный метод расчета переходных процессов
- •1.16.1. Интеграл Фурье.
- •1.16.2. Преобразование Фурье
- •1.16.3. Законы Ома и Кирхгофа для частотных спектров
- •1.16.4. Пример расчета спектральной плотности сигнала
- •ЧетырехполюсникИ
- •2.1. Общие сведения
- •2.2. Канонические формы записи уравнений четырехполюсника
- •2.3. Входное сопротивление пассивного четырехполюсника
- •2.4. Характеристическое сопротивление и постоянная передачи несимметричного четырехполюсника
- •Схемы замещения пассивного четырехполюсника
- •2.6. Способы соединения пассивных четырехполюсников
- •2.7. Передаточная функция четырехполюсника
- •2.8. Частотные электрические фильтры
- •2.8.1. Низкочастотный фильтр
- •Линии с распределенными параметрами
- •3.1. Работа линии в установившемся режиме
- •3.2. Фазовая скорость и коэффициент распространения
- •3.3. Уравнения однородной линии в гиперболических функциях
- •3.4. Нагрузочный режим работы линии
- •3.5. Короткое замыкание и холостой ход линии
- •3.6. Линия без искажения
- •3.7. Линии без потерь
- •3.8. Стоячие волны в линии
- •3.9. Линия как четырехполюсник
- •Нелинейные цепи
- •Элементы нелинейных цепей на постоянном токе, их характеристики и параметры
- •4.2. Статические и динамические характеристики нелинейных элементов
- •4.3. Расчет нелинейной электрической цепи при смешанном соединении элементов
- •4.4. Метод двух узлов
- •4.5. Стабилизация напряжения и тока с помощью нелинейных элементов
- •4.6. Метод эквивалентного генератора
- •4.7.Магнитные цепи при постоянных токах
- •4.8. Расчет магнитных цепей
- •4.9. Постоянный магнит
- •4.10. Особенности работы нелинейных элементов в цепях синусоидального тока
- •4.11. Нелинейные магнитные цепи при синусоидальных токах и напряжениях
- •4.12. Потери в стали
- •4.13. Потери на гистерезис
- •4.14. Вихревые токи
- •4.15. Влияние намагничивания на форму кривой тока и напряжения
- •4.16. Векторная диаграмма и схема замещения реальной катушки
- •4.17. Трансформатор с ферромагнитным сердечником
- •4.18. Векторная диаграмма трансформатора под нагрузкой
- •4.19. Феррорезонансные явления
- •4.20. Феррорезонанс напряжения
- •4.21. Ферромагнитный усилитель
- •4.22. Нелинейный конденсатор в цепи синусоидального тока
- •4.23. Вентиль в цепи синусоидального тока
- •4.24. Кусочно-линейная аппроксимация характеристик нелинейных элементов
- •4.25. Расчет нелинейных цепей по мгновенным значениям
- •1. Переходные процессы в линейных
- •2. Четырехполюсники………………………………………………38
- •3. Линии с распределенными параметрами……...………59
- •Курс лекций по теории электрических цепей. Ч.2
- •Издательство «нефтегазовый университет»
- •625000, Тюмень, ул. Володарского, 38
- •625039, Тюмень, ул. Киевская, 52
- •Часть 2
2.3. Входное сопротивление пассивного четырехполюсника
В случае, когда четырехполюсник включен между генератором и нагрузкой, то режим работы генератора будет существенно завесить от входного сопротивления четырехполюсника. В свою очередь, этот параметр будет зависеть от входного сопротивления четырехполюсника, а также сопротивления нагрузки ZН1 и ZН2. Для определения коэффициентов Zвх1 и Zвх2 выполняют режимы холостого хода и короткого замыкания, что упрощает исходную систему уравнений.
![]()
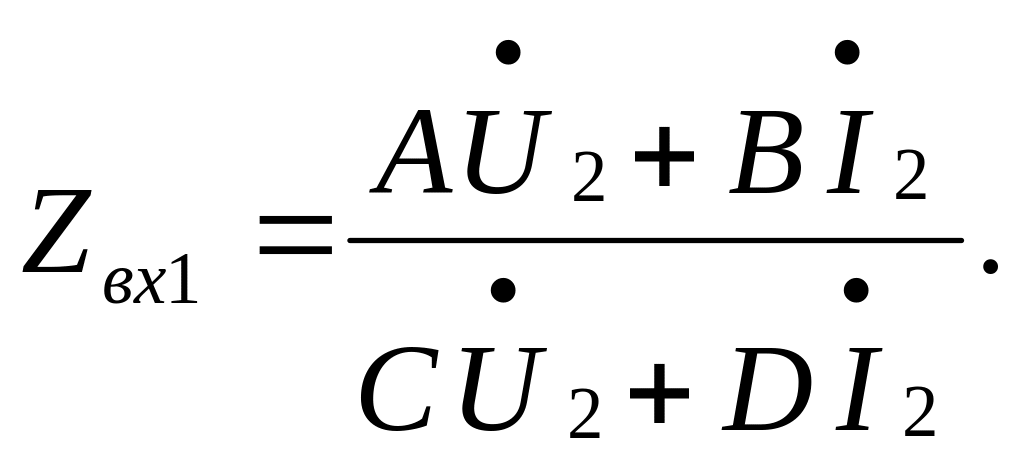
При
![]() имеем:
имеем:
![]()
При
![]() имеем:
имеем:
![]()
Аналогичные рассуждения могут быть получены при замене местами входа и выхода;
При
![]() имеем:
имеем:
![]()
При
![]() имеем:
имеем:
![]()
Между параметрами Zхх и Zк.з. может быть получено соотношение
![]() .
.
При практическом определении коэффициентов A,B,C,D через соответствующие значения сопротивления холостого хода и короткого замыкания можно воспользоваться известными методами определения комплексных входных сопротивлений. Для этого необходимо измерение напряжений, токов и мощности со стороны входных и выходных зажимов. Мощность необходимо измерять для определения угла сдвига фаз между токами и напряжениями. При этом достаточно выполнить любые три из четырех опытов для холостого хода и короткого замыкания, а затем воспользоваться уравнением связи AD – BC = 1. При работе четырехполюсника в цепи постоянного тока измерение мощности не требуется.
2.4. Характеристическое сопротивление и постоянная передачи несимметричного четырехполюсника
Характеристическим сопротивлением несимметричного четырехполюсника со стороны входных зажимов ZC1 и ZC2 называется такая пара сопротивлений, для которой при ZH = ZC2, ZВХ =ZC1 и наоборот. При этом четырехполюсник будет выполнять роль связного звена между генератором и нагрузкой. Из полученных ранее уравнений четырехполюсника определим входные сопротивления ZВХ1 и ZВХ2. Для входа при условии, что ZH =ZC2;
![]()
Аналогично можно получить при перемене клемм местами:
![]()
Совместное решение данных уравнений позволит выразить характеристическое сопротивление через параметры A,B,C,D четырехполюсника:
![]() (2.4.1)
(2.4.1)
Аналогичного рода выражение будет и для
![]()
Выделим одно из основных уравнений четырехполюсника и выполним преобразования:
![]()
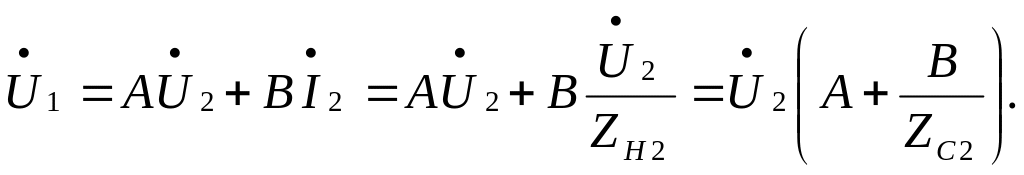
Для симметричного четырехполюсника получим:
![]()
![]()
![]() ;
;
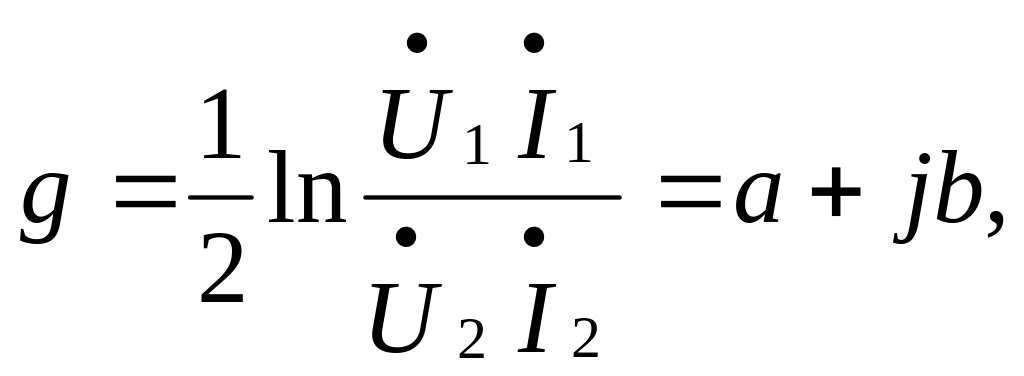 (2.4.2)
(2.4.2)
где a – коэффициент затухания четырехполюсника, b – коэффициент фазы.
 (2.4.3)
(2.4.3)
где S1 и S2 – мощности на входе и на выходе;
![]() (2.4.4)
(2.4.4)
В итоге получим:
![]()
![]()
Окончательное выражение для постоянной передачи:
![]()
Параметры g, ZC1, ZC2 носят название вторичных параметров четырехполюсника. Уравнения несимметричного четырехполюсника могут быть записаны с использованием гиперболических функций:
![]()
![]()
![]()
![]()
Учитывая выражения для Zc1 и Zc2:
![]()
![]()
Объединяя соотношения, установим взаимосвязь между коэффициентами четырёхполюсника и вторичными параметрами:
![]()
![]()
![]()
![]() (2.4.5)
(2.4.5)
При симметричном четырехполюснике уравнения упростятся в силу того, что A = D.
