
- •2. Дії над матрицями. Властивості дій над матрицями.
- •3. Визначники квадратних матриць. Способи обчислення визначників.
- •4. Визначник n-го порядку. Теорема Лапласа.
- •5. Визначники. Властивості визначників.
- •6. Мінори та алгебраїчні доповнення елементів.
- •7. Обернена матриця. Алгоритм оберненої матриці.
- •8. Ранг матриці. Властивості рангу матриці. Елементарні перетворення матриці.
- •9. Основні поняття система n лінійних алгебраїчних рівнянь з n змінними. Правило Крамера.
- •10. Матричний метод розв’язування слар. Алгоритм розв’язування системи матричним методом.
- •11.Теорема Кронекера-Капеллі. Алгоритм розв’язання слар.
- •12.Основні поняття системи m лінійних рівнянь з n змінними. Розв’язок слар методом Гаусса.
- •13.Метод Жордана-Гаусса.Алгоритм кроку перетворення Жордано-Гаусса.
- •14. Основні положення слар
- •15.Скалярний векторний добуток. Властивості векторного добутку.
- •16.Визначення мішаного добутку, його геометричний зміст.
- •17. Векторний простір, його розмірність і базис. Розклад вектора за базисом. Лінійно залежні і лінійно незалежні системи векторів.
- •18. Рівняння лінії на площині. Вивести канонічне та параметричне рівняння прямої.
- •19. Вивести рівняння прямої, що проходить через дві точки, і рівняння прямої у відрізках на осях.
- •20. Вивести векторне рівняння прямої та загальне рівняння прямої та його випадки.
- •21. Вивести нормальне рівняння прямої та рівняння пучка прямих.
- •26. Дії над матрицями. Властивості дій над матрицями.
- •27.Визначники квадратних матриць. Способи обчислення визначників.
- •28. Визначник n-ого порядку. Теорема Лапласа.
- •29.Визначники.Властивості визначників.
- •30.Мінори та алгебраїчні доповнення елементів.
- •31. Рівняння площини у просторі: за трьома точками, у відрізках на осях, нормальне.
- •32. Рівняння площини, що проходить через задану точку перпендикулярно до заданого вектора.
- •33. Кут між площинами. Умови паралельності і перпендикулярності двох площин. Відстань від точки до площини.
- •34. Різновиди рівняння в просторі: канонічне, параметричні, за двома точками. Пряма як перетин двох площин.
- •35. Кут між прямими в просторі. Кут між прямою і площиною. Умови паралельності і перпендикулярності прямої і площини. Знаходження точки перетину прямої і площини.
- •36. Поняття кривих ліній другого порядку. Дослідження рівняння другого порядку. Коло.
- •37. Еліпс: означення, рівняння, графік, вершини, півосі, фокуси, ексцентриситет, директриси.
- •38. Гіпербола: означення, рівняння, графік, спряжена гіпербола, вершини, осі, фокуси, ексцентриситет, асимптоти, директриси.
- •39. Парабола: означення, рівняння, графік,вершина, фокус, ексцентриситет, директриса. Різновиди розміщення параболи на площині та її рівняння.
- •40. Поняття числової послідовності, формула n-го члена, зростаюча, спадна, обмежена послідовність. Поняття границі числової послідовності.
- •45. Теорема про зв'язок між нескінченно малими та нескінченно великими функціями. Теорема про зв'язок між нескінченно малими функціями та границею функції.
- •123.Необхідна ознака збіжності ряду.
- •148. Лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами.
- •149.Лінійні неоднорідні рівняння другого порядку зі сталими коефіцієнтами.
- •46. Еквівалентні нескінчені малі величини. Ланцюжок еквівалентних нескінченно малих величин. Теорема про застосування еквівалентних нескінченно малих величин про обчислення границь функцій.
- •47. Властивості функцій, які мають границю в точці: єдність границі, граничний перехід у нерівності, границя проміжної фукції, обмеженість функції в точці.
- •48. Властивості границь функції: границя сталої, суми, добутку, частки функцій, границя степеневої функції.
- •49. Розкриття невизначеностей, при застосуванні ірраціональних функцій та многочленів під час обчислення границь функцій.
- •50. Перша і друга важливі границі та наслідки з них.
- •51. Неперервність функції в точці: означення Коші та означення в термінах приростів функцій та аргументу. Застосування поняття неперервності при обчисленні границь функцій.
- •52. Властивості функцій, неперервних у точці. Теорема про неперервність елементарних функцій.
- •53. Властивості функцій, неперервних на відрізку. Геометрична інтерпретація цих властивостей.
- •55. Задачі, які приводять до поняття похідної: задача про продуктивність праці, задача про кутовий коефіцієнт дотичної.
- •56. Означеня похідної. Диференційованість і неперервність функції в точці і на проміжку.
- •57. Правила диференціювання сталої, суми, добутку, частки функцій та наслідки з них.
- •59. Геометричний зміст похідної. Рівняння дотичної. Поняття нормалі до графіка функції та її рівняння. Економічний зміст похідної.
- •60. Похідна складної та оберненої функцій.
- •61. Диференціювання параметрично заданих функцій.
- •63. Похідна степенево-показникових функцій.
- •64. Похідні вищих порядків.
- •70.Екстремум функції, необхідня та достатня умови існування екстремуму.
- •71. Опуклість та вгнутість графіка функції. Необхідна і достатня умови опуклості (вгнутості) графіка функції.
- •72.Точки перегину графіка функції. Неохідна і достаня умови існування точок перегину.
- •73. Асимптоти графіка функції.
- •74.Функції кількох змінних. Основні поняття.
- •75. Функції двох змінних. Область визначення.
- •76.Лінії рівня функції двох змінних.
- •77. Частинний приріст і частинні похідні I-го порядку.
- •79. Використання повного диференціала до наближених значень.
- •80.Похідна за напрямом.
- •82.Частинні похідні вищих порядків. Теорема про рівність мішених похідних.
- •88. Частинний приріст і частинні похідні I-го порядку.
- •90. Частинні похідні вищих порядків. Теорема про рівність мішених похідних.
- •93.Обчислення наближеного значення в точці за допомогою повного диференціала.
- •94.Знаходження екстремуму ф-ції кількох змінних.
- •95. Знаходження умовного екстремуму.
- •97. Первісна для заданої функції,її осн. Властивості.
- •98. Невизначений інтеграл та його властивості.
- •99. Метод безпосереднього інтегрування невизначених інтегралів.
- •100.Знаходження невизначеного інтеграла методом заміни змінної.
- •101. Знаходження невизначеного інтеграла методом інтегрування частинами
- •104. Метод невизначених коефіцієнтів.
- •106. Інтегрування тригонометричних функцій.
- •109. Визначений інтеграл та його властивості.
- •110. Задача, що приводить до поняття визначеного інтеграла.
- •111. Формула Ньютона-Лейбніца для обчислення визначених інтегралів.
- •121. Поняття ряду. Збіжність ряду та його сума.
- •122. Властивості збіжних рядів.
- •123. Необхідна ознака збіжності ряду.
- •124. Еталонні ряди.
- •128.Радикальна ознака Коші.
- •129. Інтегральна ознака Коші.
- •130. Знакозмінні ряди. Ознака Лейбніца.
- •134. Радіус, інтервал, область збіжності ряду.
- •135. Ряд Тейлора.
- •136.Ряд Маклорена.
- •138. Використання рядів до наближених обчислень функцій.
- •139. Диференціальні рівняння. Основні поняття та означення.
- •140. Диф. Рівняння і порядку. Основіні поняття.
- •141. Диф.Рівняння з відокремлюваними змінними.
- •142.Задача Коші
- •143.Однорідні диференціальні рівняння першого порядку .
- •145. Диференціальні рівняння другого порядку. Основні поняття.
- •146. Диференціальні рівняння другого порядку, що допускають пониження порядку.
111. Формула Ньютона-Лейбніца для обчислення визначених інтегралів.
Формула Ньютона-Лейбніца дає практичний і зручний метод
обчислення визначеного інтеграла в тому випадку, коли відома первісна
від підінтегральної функції. Тільки з відкриттям цієї формули визначений
інтеграл зміг отримати те значення в математиці, яке він має сьогодні.
Обчислення визначеного інтеграла як границю інтегральної суми були
відомі ще за часів Архімеда, проте застосування цього методу
обмежувалося тими простими випадками, коли вдавалося обчислити ці
границі. Формула Ньютона-Лейбніца встановлює простий зв’язок між
первісною та визначеним інтегралом, що значно розширює область
застосування визначеного інтеграла до різних задач техніки, механіки,
астрономії і т. д.
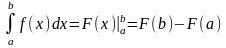
112. Метод безпосереднього інтегрування визначених інтегралів.
Цей
метод базується на рівності
![]() ,
де а та b
– сталі
і застосовується у тих випадках, коли
підінтегральна функція f
має вигляд
однієї
із підінтегральних функцій табличних
інтегралів, але її аргумент відрізняється
від змінної інтегрування постійним
доданком або постійним множником або
постійним множником та постійним
доданком.
,
де а та b
– сталі
і застосовується у тих випадках, коли
підінтегральна функція f
має вигляд
однієї
із підінтегральних функцій табличних
інтегралів, але її аргумент відрізняється
від змінної інтегрування постійним
доданком або постійним множником або
постійним множником та постійним
доданком.
113. Метод інтегрування заміни змінної у визначеному інтегралі.
Має
місце наступна формула заміни змінної
у визначеному інтегралі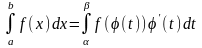 ,
,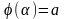 ,
,
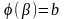 .
.
114. Метод інтегрування частинами у визначеному інтегралі.
Застосувавши формулу Ньютона-Лейбница до формули інтегрування частинами, маємо
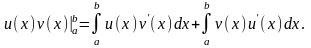
115. Застосування визначеного інтеграла до обчислення площ фігур, обмежених лініями.
Якщо
на [a,
b]
функції
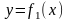 і
і
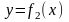 неперервні, то площа області, обмеженої
знизу графіком функції
,
зверху - графіком функції
,
зліва - прямою
неперервні, то площа області, обмеженої
знизу графіком функції
,
зверху - графіком функції
,
зліва - прямою
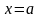 ,
справа - прямою
,
справа - прямою
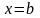 обчислюється за формулою:
обчислюється за формулою:
Якщо
на [a,
b]
функції
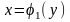 і
і
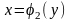 неперервні, то площа області, обмеженої
зліва графіком функції
,
справа - графіком функції
,
знизу - прямою
неперервні, то площа області, обмеженої
зліва графіком функції
,
справа - графіком функції
,
знизу - прямою
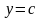 ,
зверху - прямою
,
зверху - прямою
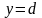 обчислюється за формулою:
обчислюється за формулою:
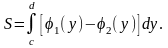
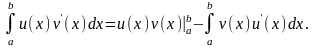
116-117. Невласний інтеграл з нескінченною верхнею межею.
Теорема. Похідна інтеграла від неперервної функції по змінній верхній межі існує і дорівнює значенню підінтегральної функції в точці, що дорівнює верхній межі.
Невласні інтеграли
Визначений інтеграл існує лише при виконанні двох умов:
1) Щоб відрізок інтегрування був скінченим;
2) Щоб підінтегральна функція f(x) була неперервною.
Якщо не виконується хоча б одна з цих двох умов, то визначений інтеграл називається невласним, причому, якщо не виконується перша умова, то такий інтеграл називається невласним інтегралом І-го роду, а якщо ж не виконується друга умова, то такий інтеграл є ІІ-го роду.
Дослідження невласних інтегралів приводять шляхом граничного переходу до визначеного інтегралу.
Якщо границі будуть існувати (дорівнюватимуть скінченому числу), то відповідні невласні інтеграли називається збіжними. Якщо ж границі не існують або дорівнюють нескінченності, то такі невласні інтеграли називаються розбіжними.
118. Визначений інтеграл існує лише при виконанні двох умов:
1) Щоб відрізок інтегрування був скінченим;
2) Щоб підінтегральна функція f(x) була неперервною.
Якщо не виконується хоча б одна з цих двох умов, то визначений інтеграл називається невласним, причому, якщо не виконується перша умова, то такий інтеграл називається невласним інтегралом І-го роду, а якщо ж не виконується друга умова, то такий інтеграл є ІІ-го роду.
119.
Нехай функція
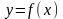 визначена і неперервна при
визначена і неперервна при
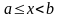 ,
а при
функція або не визначена, або терпить
розрив. У цьому випадку не можна говорити
про інтеграл
,
а при
функція або не визначена, або терпить
розрив. У цьому випадку не можна говорити
про інтеграл
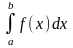 як про границю інтегральних сум, тому
що
не визначена на відрізку
як про границю інтегральних сум, тому
що
не визначена на відрізку
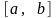 ,
і тому ця границя може і не існувати.
,
і тому ця границя може і не існувати.
Інтеграл
від функції
,
необмеженої в точці b,
означається таким способом:
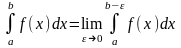 .
.
Означення. Якщо границя, яка стоїть справа, існує, то інтеграл називають невласним збіжним інтегралом, у противному випадку інтеграл називають розбіжним.
120. Метод найменших квадратів — метод знаходження наближеного розв'язку надлишково-визначеної системи. Часто застосовується в регресійному аналізі. На практиці найчастіше використовується лінійний метод найменших квадратів, що використовується у випадку системи лінійних рівнянь.
