28. Визначник n-ого порядку. Теорема Лапласа.

Матрицю А n-ого порядку можна поставити у відповідність число det A (або , або ), яке називають визначником цієї матриці.

1.При n = 1 А=( ), det A =

2.При n = 2 А = ( ), det A= = -

Визначник матриці А також назив. її детермінантом.

Теорема Лапласа. Визначник n-ого порядку дорівнює сумі добутків елементів будь-якого рядка чи стовпця на їх алгебраїчні доповнення: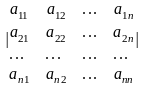

Квадратній матриці А n-го порядку можна поставити у відповідність число detА,яке називається визначником цієї матриці. Правило Лапласа:Визначник дорівнює сумі добутків елементів будь-якого рядка (стовпця )помноженні на відповідні алгебраїчні доповнення. Алгебраїчні доповнення Аij елемента aij

називають мінор цього елемента ,взятий із знаком «плюс»,якщо сума номерів рядка і стовпчика –число парне ,та зі знаком «мінус»,якщо непарне.Мінором Мij елемента aij визначника n-го порядку називається визначник ( n-1)-го порядку,який одержимо з даного визначника шляхом викреслювання і-го рядка та j-го стовпця,на пнрнтині яких знаходиться елемент aij.

29.Визначники.Властивості визначників.

Квадратній матриці А n-ого порядку можна поставити у відповідність число det A (або , або ), яке називають визначником цієї матриці.

1.При n = 1 А=( ), det A =

2.При n = 2 А = ( ), det A= = -

Визначник матриці А також назив. її детермінантом.Властивості:

1.Величина визначника не зміниться, якщо всі рядки змінити на стовпці з тим самим номером.

2.Перестановка двох стовпців або рядків визначника рівносильна множенню визначника на (-1)

3.Якщо визначник має два рівні стовпці чи рядки, то він дорівнює нулю.

4.Множення всіх елементів деякого рядка чи стовпця деякого рядка чи стовпця визначника на число k рівносильне множенню визначника на це число.

5.Якщо всі елементи деякого рядка чи стовпця визначника дорівнюють нулю, то визначник дорівнює нулю.

6.Якщо відповідні елементи двох стовпців чи рядків визначника пропорційні, то визначник дорівнює нулю.

7.Якщо кожен елемент деякого рядка чи стовпця визначника являє собою суму двох доданків, то визначник можна подати у вигляді суми двох визначників.

8.Якщо до елементів деякого рядка чи стовпця додати відповідні елементи іншого рядка чи стовпця, помножені на спільний множник, то величина визначника не зміниться.

30.Мінори та алгебраїчні доповнення елементів.

Мінором елемента визначника n-ого порядку називається визначник (n-1)-ого порядку , який одержимо з даного визначника шляхом викреслювання i-ого рядка та j-ого стовпця, на перетині яких знаходиться елемент .

Алгебраїчним доповненням елемента визначника назив. мінор цього елемента, взятий із знаком «+» , якщо сума номерів рядка і стовпчика – число парне, та зі знаком

«-», якщо – непарне.

31. Рівняння площини у просторі: за трьома точками, у відрізках на осях, нормальне.

.

32. Рівняння площини, що проходить через задану точку перпендикулярно до заданого вектора.

Покажемо, що алгебраїчною поверхнею першого порядку є площина. Для цього доведемо такі теореми.

Теорема 1. Площина в прямокутній декартовій системі координат визначається загальним рівнянням першого степеня відносно поточних координат.

Доведення. Геометричне будь-яку площину в просторі XYZ можна задати за допомогою вектора , перпендикуляр¬ного до цієї площини, і точки M0 (x0, y0, z0), Через яку проходить дана площина

Візьмемо довільну точку M (х, у, z) і знайдемо вектор . Точка M належить заданій площині тоді і тільки тоді, коли

Оскільки то скалярний добуток мо¬жна записати у вигляді

А(х – х0) + В(у – у0) + C(z – z0) = 0,або

Ах + By + Cz - (Aх0 + Ву0 + Cz0) = 0.

Позначивши - (AX0 + Ву0 + Cz0) = D

дістанемо загальне алгебраїчне рівняння першого степеня:

Ах + By + Cz + D = О,

Отже, будь-яка площина в декартових прямокутних координатах може бути зображена рівнянням першого степеня.

Зауважимо, що рівняння (1) є рівнянням площини, яка проходить

Через точкуу M0 (х0, у0, z0) перпендикулярно до вектора = (А, В, С). Доведемо тепер обернену теорему.

Теорема 2. Загальне рівняння першого степеня

Ax + By + Cz + D = 0,

де А, В, С і D — довільні дійсні чи¬сла; х, у, z — поточні координата, визначає в декартовій прямокутній системі координат площину. Доведення. Доберемо трійку чисел (х0, y0> z0), які задовольняють рівняння (3). Це можна зробити таким чином. Два числа х0 і у0 візьмемо довільно, а третє z0 знайдемо з рівняння (3). Тоді ,

Ах0 + Ву0 + Cz0 + D = 0.

Віднімаючи від рівняння (3) рівняння (4), дістаємо

А(х – х0) + В(у – у0) + C(z – z0) = 0.

Це рівняння є рівнянням площини, перпендикулярної до вектора = (А, В, С) і такої, що проходить через точку M0 (х0, у0, z0). Таким чином, кожна площина є поверхнею першого порядку, і, навпаки, кожна поверхня першого порядку є площиною. Тому рівняння (l) або (3) називається загальним рівнянням площини.

називається векторним рівнянням площини. Враховуючи, що векторне рівняння площини запишемо у вигляді:

Якщо у загальному рівнянні площини покласти z – z0 = 0, то ді¬станемо рівняння,

А(х – х0) + В(у – у0) = 0,або

Ах + By + С = 0,

де С = - (Ax0 + Ву0). Рівняння ( 7) називається загальним рів¬нянням прямої, що лежить у площині хОу.

Дослідження загального рівняння площини

Розглянемо загальне рівняння площини

Ах + Вy + Cz + D = 0.

де А, В, С і D — довільні числа, причому хоча б одне з перших трьох відмінне від нуля.

Дослідимо окремі випадки цього рівняння.

Якщо D = О, то рівняння (8) набирає вигляду;

Ах + By + Cz = 0.

Це рівняння задовольняє точка О (0, 0, 0). Отже, рівняння (9) визначає площину, яка проходить через початок координат.

Якщо А = 0, то рівняння (8) має вигляд:

By + Cz + D = О

і визначає площину, нормальний вектор якої = (О, В, С) перпендикулярний до осі Ох. Отже, рівняння (10) визначає площину, паралельну осі абсцис, або перпендикулярну до площини yOz.

Якщо А = В = 0, а С 0, то маємо рівняння площини, паралельної хОу:

Рівняння х = 0, у = 0, z = 0 визначають відповідно координатні площини yOz, xOz, хОу.