60. Похідна складної та оберненої функцій.

Якщо аргументом функції є функція,тобто y=f(z), де z=φ(x),то функція y=f[φ(x)] називається складною.Функція f(z) називається зовнішньою,а φ(x) внутрішньою або проміжним аргументом.Т.Якщо y=f(z), z=φ(x)- диференційовані функції від своєх аргументів,то похідна складеної функції існує і дорівнює добутку похідної зовнішньої функції по проміжку аргументу на похідну проміжного аргументу за залежною змінною:y’=f’[φ(x)] φ’(x).

Для диференційованої функції з похідною,що не дорівнює 0,похідна оберненої функції = оберненій величині похідної даної функції:

61. Диференціювання параметрично заданих функцій.

Функція задана у вигляді 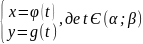, є параметрично заданою.

Якщо функція у від х задана параметрично 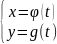, де - диференційовні функції і 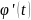≠0, то похідна цієї функції

62. Диференціювання неявно заданих функцій.

Функція у від х задана неявно,якщо вона має вигляд F(x,y)=0, не розв’язана відносно змінної у.

Алгоритм диференціювання неявно заданих функцій

1. Продиференціювати F(x,y)=0 по х, розглядаючи у як складну функцію х.

2. Розв’язати одержане рівняння відносно .

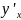63. Похідна степенево-показникових функцій.

Степенево-показниковою функцією наз. Функцію виду y= .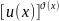

Алгоритм диференціюваня степенево-показникових функцій.

1. Прологарифмувати дану функцію з основою е: ln y = .

2. Продиференціювати обидві частини рівності, враховуючи, що ln y i ln u – складні функції: .

3. Визначити похідну функції у, враховуючи, що y= , y’=

64. Похідні вищих порядків.

Похідну n-го порядку називають похідну від похідної (n-1)-го порядку.

Для позначення похідних більш високо порядку використовують арбські цифри в душках .

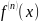65. Диференціал та його властивості.

Головну лінійну відносно 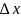частину приросту функції називають диференціалом функції і позначають dy=f’(x)dx.

Властивості:

1. Диференціал сталої дорівнює 0 (dc=0)

2. Cталий множник можна виносити за знак диференціала: dcu=cdu

3. Диференціал суми дорівнює сумі диференціалів: d(u±v)=du±dv

4. Диференціал добутку дорівнюэ добутку диференціала першого множника на другий та добутку першого на диференціал другого: d(uv)=vdu+udv

5. Диференціал частки: = .

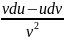6. Диференціал складної функції : dy= .

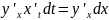66. Застосування диференціала до наближених обчислень.

67. Правило Лопіталя.

Нехай функції f(x) та g(x) визначені та диференційовані в околі точки 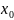, частка в точці має невизначеність або [ ], існує 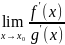, тоді існує і виконується умова .

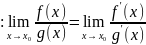68. Застосування правила Лопіталя у невизначеностях виду (0* .

У невизначеностях виду (0*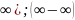 спочатку потрібно за допомогою алгебраїчних перетворень звести до невизначеностей виду або [ ], а потім застосувати правило Лопіталя.

Невизначеності виду зводять до невизначеностей виду або [ ] шляхом логарифмування.

69. Необхідня і достатня ознаки зростання (спадання) функції.

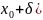Функція f(x) називаэться зростаючою(спадною ) в точці , якщо існує окіл точки ( - такий що для всіх х є ( - ) виконуэться нерівність f(x)<f( ) ( f(x)>f( )) і для всіх х є ( ; f(x)>f( (f(x)<f( ).

Необхідна ознака зростання (спадання) функції

Якщо диференційовна на деякому проміжку функція зростає(спадає) на цьому проміжку,то f’(x)>0(f’(x)<0)

Достатня ознака зротсання функції

Якщо f’(x)>0(f’(x)<0) для всіх х є (а;b), то функція зростає(спадає)на проміжку (a;b).