70,Характеристики смеси: плотность, скорость (барицентрическая, среднемассовая, диффузионная;

В каждой точке объема, занятого смесью, будет определено N плотностей ρ_i, N скоростей и т.д. Параметры для смеси в целом имеют вид:

плотность смеси - 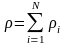; среднемассовая скорость - 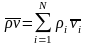(она же носит название барицентрическая скорость). Для удобства оценок эффектов переноса вводят диффузионные скорости - это скорости движения составляющих относительно центра масс смеси: 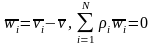Массовая скорость

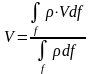
71. Виды движения сплошных сред: неустановившееся, пространственное, плоское, одномерное.

Если провести нормальное к оси трубы сечения, то во всех таких сечениях распределения скоростей одинаковы, а давление меняется только от сечения к сечению, сохраняя в данном сечении одинаковое значение. Такое движение называется установившимся. Неустановившееся соответственно наоборот.

Одномерная модель – модель, в которой поток среды описывается средними по сечению характеристиками – скоростью, плотностью, давлением, температурой и т.д., при этом все характеристики течения зависят только от координаты x сечения и от времени t.

Двумерная модель – модель, в которой поток среды описывается средними по сечению характеристиками – скоростью, плотностью, давлением, температурой и т.д., при этом все характеристики течения зависят от 2 координат x,y и от времени t.

Трехмерная модель – модель, в которой поток среды описывается средними по сечению характеристиками – скоростью, плотностью, давлением, температурой и т.д., при этом все характеристики течения зависят от 3 координат x,y,z и от времени t.

72. Понятие о методах описания физических процессов, свойств, взаимодействий и движений материальных сред. Их достоинства и недостатки.

Все явления природы на основе представлений современной физики могут быть описаны 2-мя методами: феноменологическим и статистическим.

Метод описания процесса, игнорирующий микроскопическую структуру вещества и рассматривающий его как сплошную среду (континуум) называется. феноменологическим ФМ (fenomenus – гр. явление). ФМ дает возможность установить некоторые общие соотношения между параметрами, характеризующими рассматриваемое явление в целом. Здесь законы носят общий характер, причем роль физической среды учитывается через коэффициенты (т/ф свойства), полученные из опыта. С этой точки зрения законы Фурье, Ньютона, Ома и.д. – Ф законы.

Статистический метод (СМ) – способ изучения физических явлений на основе исследования внутренней структуры вещества и обобщения их в макросвязи. Задача СМ – получение макроскопических характеристик по микроскопическим свойствам среды.

Замечание (Достоинства и недостатки ФМ и СМ).

Достоинство ФМ – в установлении общих связей между параметрами процесса с использованием эмпирической информации о процессе. Причем точность метода предопределена точностью данных из опыта.

Недостаток ФМ – в наличии эмпирической информации, что ограничивает область применимости феноменологических законов рамками эксперимента.

Достоинство СМ – в получении искомых соотношений (законов) по заданным свойствам микроскопической структуры среды без дополнительного эксперимента. Здесь среда рассматривается как некоторая система, состоящая из огромного числа молекул, ионов, атомов с заданными свойствами.

Недостаток СМ – сложность обобщения этих зависимостей и проблемы реализации метода, т.к. необходимо знать ряд параметров, которые могут быть определены в специальных разделах физики, химии, биологии и др. областях знаний.

73. Понятие о жидкости (газе), как сплошной среды. Теплофизические свойства капельных, газообразных сред

Жидкостью будем называть СС, обладающую свойством текучести, т.е. допускающую неограниченное изменение формы под действием сколь угодно малых сил.

Жидкость бывает 2-х видов: 1.Несжим-я (капельная ρ=const); 2.Сжим-я (газообразная ρ#const; ρ(P,T) )

В гидравлике принято жидкость считать сплошной средой состоящей из отдельных частиц, т. е. жидкость представляет собой макроструктуру. В капельной жидкости расстояние между частицами весьма малы, поэтому силы сцепления велики. А у газов расстояние между частицами велики, поэтому силы сцепления являются малыми.

Основные теплофизические свойства жидкости:

1. Плотность Плотность (ρ) характеризует количество покоящейся массы (m) вещества, выраженной в единице объёма (w), [кг/м³; г/см³] [ρ] = Кг / м³ ρ = m / w где m – масса, w – объем

Удельный вес [γ] = Н / м² γ = (m * g) / w где g – ускорение свободного падения

2.Сжимаемость

Коэф. сжимаемости [β_р] = 1 / Па β_р = (1 / w)*(dw / dp) Модуль упругости [E] = Па Е = 1 / β_р

Коэф. температурного расширения [β_т] = 1 / °С β_т = (1 / w)*(dw / dт)

3. Вязкость - свойство жидкости или газа оказывать сопротивление перемещению одних ее частиц относительно других. Вязкость зависит от силы взаимодействия между молекулами жидкости (газа).

Для характеристики этих сил используется коэффициент динамической вязкости ( )

Динамическая вязкость определяется по уравнению Ньютона: F / A = μ *(dv / dy) где, А – площадь перемещающихся слоёв жидкости; F – сила, требующаяся для поддержания разницы скоростей движения между слоями на величину dv; dy – расстояние между движущимися слоями жидкости; dv – разность скоростей движущихся слоёв жидкости; μ – коэффициент пропорциональности, динамическая вязкость. Величина dx/dy характеризует сдвиг (γ) слоев, деформацию. Соотношение F/A – есть величина касательного напряжения (τ), развиваемое в движущихся слоях жидкости.

Размерность динамической вязкости определяется из уравнения Ньютона:

• система СИ → [Пас, мПас]; 1 сПз = 10^–3∙кг/м ∙с = 10^–3∙Па ∙с; [μ] = Н * с / м².

За единицу динамической вязкости принят паскаль-секунда (Па- с), т.е. вязкость такой жидкости, в которой на 1 м² поверхности слоя действует сила, равная одному ньютону, если скорость между слоями на расстоянии 1 см изменяется на 1 см/с. Вязкость жидкости характеризуется также коэффициентом кине­матической вязкости, которая характеризует свойство жидкости оказывать сопротивление перемещению одной части жидкости относительно другой с учётом силы тяжести: т.е. отношением динамической вязкости к плотности жидкости. [ν] = м² / c; ν = μ / ρ

За единицу в этом случае принят м²/с. Из анализа следует, что с возрастанием температуры средняя длина свободного пробега молекул и средняя скорость движения молекул увеличиваются, а, следовательно, и вязкость газа возрастает, несмотря на уменьшение величины плотности.

Вязкость сильно зависит от Т и слабо от Р. У капельной жидкости с повышением Т вязкость уменьшается, а у газообразной - наоборот. В гидравлике существует понятие идеальной жидкости – это жидкость, которая не существует в природе, вязкость которой равна нулю, поэтому при движении такой жидкости отсутствуют силы трения.

Единицы измерения кинематической вязкости: система СИ→ [м²/с, см²/с, мм²/с]; 1сСт = 10^–2 Ст = 10^–6 м²/с = 1мм²/с. Текучесть () – это величина обратная вязкости и связанная с ней соотношением: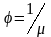 . Под теплоёмкостью (c_р) понимается количество теплоты (dQ), которое необходимо передать единице массы этого вещества (М), чтобы повысить его температуру (dT) на 1 Цельсия или Кельвина c_р = dQ / M · dT

Величина теплоёмкости зависит от температуры, поэтому каждое её значение необходимо относить к определенной температуре (с_t) или к интервалу температур. Для повышения температуры нефти объёма V плотностью ρ от температуры Т₁ до Т₂ необходимо затратить количество энергии Q, рав­ное: Q =ρ·c·(Т₂ – Т₁)·V.

Теплопроводность определяет перенос энергии от более нагретых участков жидкости к более холодным. Коэффициент теплопроводности () описывается законом теплопроводности Фурье и характеризует количество теплоты (dQ), переносимой в веществе через единицу площади (S) в единицу времени (t) при градиенте температуры (dT/dx), равном единице:

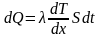
74. Понятие о многокомпонентных и многофазных средах. Определение однородной и неоднородной, изотропной и анизотропной сплошной среды.

Сплошная среда – это среда, которую допустимо рассматривать как непрерывную, пренебрегая дискретным ее строением. Однородная СС – это СС, в разных точках которой ее физические свойства одинаковы при одинаковых значениях температуры и давлении. Неоднородная СС – это СС, в разных точках которой ее физические свойства различны при одинаковых температуре и давлении. Изотропная СС – это СС, физические свойства которой не зависят от направления к изменению процессов в пространстве. Анизотропная СС – СС, физические свойства которой различны по разным направления (существенно зависят от ориентации тела в пространстве, т.е. зависят от выбранного направления к изменениям в пространстве). Однофазная СС – СС одно- или многокомпонентная, физические свойства которой в пространстве могут изменяться только непрерывно. Многофазная СС – СС одно- или многокомпонентная, состоящая из ряда однофазных частей, на границах которой ее физические свойства меняются скачкообразно

75. Простейшие модели жидких и газообразных сплошных сред: идеальная, вязкая, несжимаемая, сжимаемая , ньютоновская , упругая, с тепловым расширением, совершенного и реального газов.

Идеальная жидкость Определение. ИЖ – это жидкость, в которой напряжения, действующего на любую площадку с нормалью , направлен площадке. Иначе, в ИЖ имеются только нормальные напряжения и отсутствуют касательные. Замечание. Реальные СС имеют касательные напряжения. Эти касательные напряжения =0 только в состоянии покоя или если СС движется как абсолютное твердое тело. Тогда РСС – идеальная, т.е. без трения.

Вязкая ньютоновская жикость Наличие касательных напряжений и прилипания жидкости к стенке отличают РСС от ИС. В модели вязкой жидкости предполагается, что касательное напряжение τ между слоями движущейся жидкости пропорционально разности скоростей этих слоев, рассчитанной на единицу расстояния между ними, а именно - градиенту скоростей: 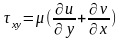; Вязкость нефти и почти всех нефтепродуктов зависит от температуры. При повышении температуру вязкость уменьшается, при понижении - увеличивается. Для расчета зависимости вязкости, например, кинематической v от температуры Т используются различные формулы, в том числе и формула Рейнольдса-Филонова.

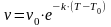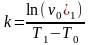; в которой v₀ - кинематическая вязкость жидкости при температуре Т_0, а к- опытный коэффициент.

Модель несжимаемой жидкости Жидкость называется несжимаемой, если ее плотность не меняется в процессе движения: dp/dl = 0. причем если изначально у всех частиц жидкости эта плотность была одинакова (однородная жидкость), то она остается таковой во всё время движения: р = р₀ = const.

Конечно, несжимаемая жидкость - это только модель реальной среды, ибо, как известно, абсолютно несжимаемых сред нет.

В общей форме модель ньютоновской несжимаемой вязкой жидкости .

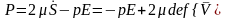Модель упругой сжимаемой жидкости Существуют ряд процессов, в которых необходимо учитывать хотя и малые изменения плотности жидкости. Для этого часто используют модель так называемой упругой жидкости. В этой модели плотность жидкости зависит от давления согласно формуле р(р) = Ро[1 + β(Р-Ро)]

в которой β(1/Па) - коэффициент сжимаемости; ρ₀-плотность жидкости при нормальном давлении Р₀.

Используется также модуль упругости К (Па), который равен 1/β. Тогда формула (2.5) приобретает вид 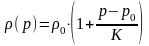Неньютоновские жидкости. Определение. Жидкости, моделируемые условием 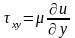- наз. ньютоновскими вязкими жидкостями; 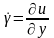-градиент скорости. Существуют среды, в которых связь τ=f( ) – нелинейная. Это неньютоновские среды. Здесь связь между τ в слоях жидкости степенная

Кажущаяся вязкость в среде – где k, n – коэффициенты в среде.

Определение. Если n<1, то жидкости называются псевдопластичными (суспензии, вязкие жидкости с взвесью мелких частиц). При n>1 – среды – дилатантные (крахмальный клейстер).

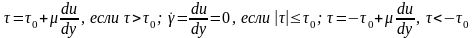. (6)

Физический смысл (6). Пока τ не превышает по mod некоторую предельную величину τ₀ (является предельным напряжением сдвига), течение такой среды не начинается (в этом случае =0). Среда течет как вязкая жидкость, если 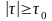, при этом .

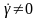Модель жидкости с тепловым расширением То, что различные среды при нагревании расширяются, а при охлаждении сжимаются, учитываются в модели жидкости с объемным расширением. В этой модели плотность ρ есть функция от температуры Т, так что ρ = ρ(Т):

ρ(Т) = ρ ₀[1 + ξ(Т₀-Т)], (2.6)

в которой ξ(1/°С)-коэффициент объемного расширения, а ρ₀ и Т₀-плотность и температура жидкости при нормальных условиях.

Из формулы (2.6) следует, в частости, что при нагревании, т.е. в тех случаях, когда Т>Т₀. р<р₀- жидкость расширяется; а в тех случаях, когда Т<Т₀, р>р₀- жидкость сжимается.

Модель совершенного газа Для характеристики термодинамического состояния газов в указанной области давлений и температур используется модель совершенного газа. 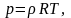(Менделеева-Клайперона) где единственная входящая в уравнение константа R называется газовой постоянной, причем R = R₀/μ_г, . R₀, - универсальная газовая постоянная, равная 8314 Дж/(моль К). Таким образом, для совершенных газов все газовые постоянные зависят только от молекулярного веса. Модель совершенного газа достаточно эффективно работает в интервале не слишком высоких давлений и умеренных температур.

Модель реального газа Газ – реальный (РГ) - это газ, между молекулами которого существуют заметные силы межмолекулярного взаимодействия.Общая запись модели РГ 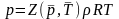, где 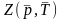- коэффициент сверхсжимаемости, функуция от 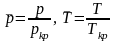. Таким образом модель учитывает не только молекулярный вес газа (через константу R), но и такие термодинамические постоянные, как его критические давление и температуру. Очевидно также, что для умеренных давлений и температур Z=1 и модель естественным образом трансформируется в модель совершенного газа. Для реального газа Z < 1

76. Уравнение Бернулли для идеальной и вязкой жидкости. Геометрическая и энергетическая интерпретация слагаемых уравнения Бернулли.

За основу гидравлических расчетов трубопроводов принимается уравнение Бернулли, частный случай выражения закона сохранения энергии, которое для идеальной жидкости имеет вид:

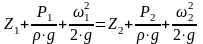(4.6)

где Р₁, Р₂ - давления в сечениях 1 и 2, Па;

ρ- плотность, кг/м³;

ω₁, ω₂, - средние линейные скорости в сечениях 1 и 2, м/с;

g- ускорение свободного падения, м/с².

Каждый член уравнения (4.6) имеет размерность высоты и носит соответствующее название:

Zi - определяет высоту положения различных точек линии тока над плоскостью сравнения, геометрический напор; удельная потенциальная энергия положения.

- называется пьезометрическим напором (пьезометрической высотой),

представляет собой высоту, на которую могла бы подняться жидкость при отсутствии движения

- носит название скоростного напора.

- носит название гидродинамического напора

Уравнение Бернулли является выражением закона сохранения механической энер­гии движущейся жидкости, по этой причине все части уравнения представляют собой ве­личины удельной энергии жидкости:

z - удельная энергия положения,

- удельная энергия давления,

- удельная потенциальная энергия,

- удельная кинетическая энергия

- удельная механическая энергия.

Сумма всех трех напоров определяет запас полной механической энергии потока в соответствующем сечении, отнесенной к единице силы тяжести, и называется полным напором H:

(4.7)

Реальная жидкость обладает вязкостью. В уравнении Бернулли появляется слагаемое, учитывающее потери энергии вследствие гидравлических сопротивлений на участке 1-2:

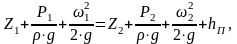(4.8)

где h_П– напор на преодоление путевых сопротивлений, то есть на преодоление сил трения и местных сопротивлений трубопроводов.

h_П=h_Т + h_М, (4.9)

где h_Т – потеря напора за счет преодоления сил трения по длине трубопровода;

h_М - потеря напора за счет местных сопротивлений.

При Z₁ =Z₂ и ω₁= ω₂

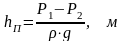(4.10)

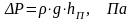
Напорная линия всегда падает, а пьезометрическая может опускаться и подниматься ( по направлению потока). Подъем линии должен быть в местах увеличения площадей поперечных

сечений потока, где скорость уменьшается, а давление увеличивается.

77. Термодинамические силы и потоки. Законы молекулярного переноса тепла и массы в исследовании процессов тепломассообмена в сплошных средах.

Производство энтропии системы является диссипативной функцией и представляет собой сумму произведений термодинамических потоков Ji на термодинамические движущие силы Xi необратимых процессов, протекающих в системе:

Энтропи́я — понятие, впервые введённое в термодинамике для определения меры необратимого рассеивания энергии

Под термодинамической движущей силой понимают разность каких-либо потенциалов (концентраций, температур, давлений и т.д.), которая вызывает протекание соответствующего процесса, является его причиной. Под термодинамическим потоком - количественное выражение процесса, изменение характеризующей его величины за единицу времени.

Перенос энергии от более нагретых участков тела к менее нагретым в результате теплового движения и взаимодействия составляющих его частиц. Приводит к выравниванию температуры тела. Обычно количество переносимой энергии, определяемое как плотность теплового потока, пропорционально градиенту температуры -закон Фурье. Коэффициент пропорциональности называют коэффициентом теплопроводности.

Теплопрово́дность — это перенос теплоты структурными частицами вещества (молекулами, атомами, электронами) в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.

закон теплопроводности Фурье, где Q – теплота, передаваемая посредством теплопроводности через площадь S за время t, - градиент температуры, - теплопроводность. , где Ср – удельная теплоемкость при постоянном давлении, где Pr - число Прандтля - физическая характеристика среды и зависит только от её термодинамического состояния

МАССООБМEН, необратимый перенос массы компонента смеси в пределах одной или несколько фаз. Осуществляется в результате хаотич. движения молекул (мол. диффузия), макроскопич. движения всей среды (конвективный перенос), а в турбулентных потоках - также в результате хаотич. движения вихрей различные размера. МАССООБМEН включает массоотдачу (перенос вещества от границы раздела в глубь фазы) и массопередачу (перенос вещества из одной фазы в другую через поверхность раздела фаз).

Во всех случаях диффузия идет из слоя золя с более высокой концентрацией частиц до полного выравнивания их концентраций во всех частях системы. Если обозначить dm количество вещества, перенесенного через сечение S по направлению x за время dt, то в соответствии с первым законом А. Фика :

где dm – количество вещества, диффуидирующего в единицу времени;

S – площадь сечения; dc/dx – градиент концентрации; D – коэффициент диффузии;

Знак «минус» показывает, что процесс идет в сторону уменьшения концентрации.