5.2.2 Анализ поиска в ширину

Оценим время работы описанной процедуры. В процессе работы вершины только темнеют, так что каждая вершина кладётся в очередь не более одного раза (благодаря проверке в строке 12). Следовательно, и вынуть её можно только один раз. Каждая операция с очередью требует O (1) шагов, так что всего на операции с очередью уходит время O(V). Теперь заметим, что список смежных вершин просматривается, лишь когда вершина извлекается из очереди, то есть не более одного раза. Сумма длин всех этих списков равна |Е| (2|Е| для неориентированного графа) и всего на их обработку уйдёт время O(Е). Инициализация требует O(V) шагов, так что всего полу- чается O(V + Е). Тем самым время работы процедуры BFS пропорционально размеру представления графа G в виде списков смежных вершин.

Поиск в ширину для полного обхода графа с n вершинами и m дугами требует столько же времени, как и поиск в глубину, то есть времени порядка O(max(n, m)). Поскольку обычно m  n, то получается O(m).

5.2.3 Деревья поиска в ширину

В ходе работы процедуры BFS выделяется некоторый подграф – дерево поиска в ширину, задаваемое полями [v]. Более формально, применим процеду- ру BFS к графу G = (V, Е) с начальной вершиной s. Рассмотрим подграф, вершинами которого являются достижимые из s вершины, а рёбрами являются рёбра ([v], v) для всех достижимых v, кроме s.

Лемма 5.1. Построенный таким образом подграф графа G представляет собой дерево, в котором для каждой вершины v имеется единственный простой путь из s в v. Этот путь будет кратчайшим путём из s в v в графе G.

Доказательство. Существование пути из s в и (как и то, что он будет крат- чайшим) следует из теоремы 5.1. (индукция по расстоянию от s до v). Поэтому граф связен. Поскольку число рёбер в нём на единицу меньше числа вершин, то он является деревом.

Дерево называется подграфом предшествования (predecessor subgraph), а также деревом поиска в ширину (breadth-first tree) для данного графа и данной начальной вершины. (Заметим, что построенное дерево зависит от того, в каком порядке просматриваются вершины в списках смежных вершин.)

Если значения полей уже вычислены с помощью процедуры BFS, то крат- чайшие пути из s легко найти: их печатает процедура PRINT-PATH.

Листинг 5.3 – Поиск в глубину

Время выполнения пропорционально длине печатаемого пути (каждый рекурсивный вызов уменьшает расстояние от s на единицу).

5.2.4 Поиск в глубину

Поиск в глубину является обобщением метода обхода дерева в прямом порядке. Предположим, что есть ориентированный граф G, в котором первоначально все вершины помечены как непосещенные. Поиск в глубину начинается с выбора начальной вершины v графа G, и эта вершина помечается как посещенная. Затем для каждой вершины, смежной с вершиной v и которая не посещалась ранее, рекурсивно применяется поиск в глубину. Когда все вершины, которые можно достичь из вершины v, будут «удостоены» посещения, поиск заканчивается. Если некоторые вершины остались не посещенными, то выбирается одна из них и поиск повторяется. Этот процесс продолжается до тех пор, пока обходом не будут охвачены все вершины орграфа G.

Этот метод обхода вершин орграфа называется поиском в глубину, поскольку поиск непосещенных вершин идет в направлении вперед (вглубь) до тех пор, пока это возможно. Например, пусть x – последняя посещенная вершина. Для продолжения процесса выбирается какая-либо нерассмотренная дуга x  y, выходящая из вершины x. Если вершина y уже посещалась, то ищется другая вершина, смежная с вершиной x. Если вершина y ранее не посещалась, то она помечается как посещенная и поиск начинается заново от вершины y. Пройдя все пути, которые начинаются в вершине y, возвращаемся в вершину x, то есть в ту вершину, из которой впервые была достигнута вершина y. Затем продолжается выбор нерассмотренных дуг, исходящих из вершины x, и так до тех пор, пока не будут исчерпаны все эти дуги.

Для представления вершин, смежных с вершиной v, можно использовать список смежных, а для определения вершин, которые ранее посещались, – массив Visited:

Graph: TAdjacencyList;

Visited: array[1..n] of boolean;

Чтобы применить эту процедуру к графу, состоящему из n вершин, надо сначала присвоить всем элементам массива Visited значение false, затем начать поиск в глубину для каждой вершины, помеченной как false.

procedure DepthSearch(v: integer);

begin

Visited[v] := true;

for каждой вершины y, смежной с v do

if not Visited[y] then

DepthSearch(y);

end;

begin

while есть непомеченные вершины do begin

v := любая непомеченная вершина;

DepthSearch(v);

end;

end.

Листинг 5.4 – Поиск в глубину

Листинг 5.5 – Поиск в глубину

Как и при поиске в ширину, обнаружив (впервые) вершину v, смежную с и, мы отмечаем это событие, помещая в поле [v] значение и. Получается дерево - или несколько деревьев, если поиск повторяется из нескольких вершин. Говоря дальше о поиске в глубину, мы всегда будем предполагать, что так и дела- ется (поиск повторяется). Мы получаем подграф предшествования (predecessor subgraph), определённый так: , где

Подграф предшествования представляет собой лес поиска в глубину (depth-first forest), состоящий из деревьев поиска в глубину (deep-first trees).

Алгоритм поиска в глубину также использует цвета вершин. Каждая из вершин вначале белая. Будучи обнаруженной (discovered), она становится серой; она станет чёрной, когда будет полностью обработана (finished), то есть когда список смежных с ней вершин будет просмотрен. Каждая вершина попадает ровно в одно дерево поиска в глубину, так что эти деревья не пересекаются.

Помимо этого, поиск в глубину ставит на вершинах метки времени (times- tamps). Каждая вершина имеет две метки: в d[v] записано, когда эта вершина была обнаружена (и сделана серой), а в f [v] – когда была закончена обработка списка смежных с v вершин (и v стала чёрной).

Эти метки времени используются во многих алгоритмах на графах и по- лезны для анализа свойств поиска в глубину.

В приводимой далее процедуре DFS (Depth-First Search – поиск в глубину) метки времени d[v] и f[v] являются целыми числами от 1 до 2|V|; для любой вершины и выполнено неравенство

d[u] < f[u]

Вершина и будет БЕЛОЙ до момента d[u], СЕРОЙ между d[u] и f[u] и ЧЁРНОЙ после f[u].

Исходный граф может быть ориентированным или неориентированным. Пе- ременная time – глобальная переменная текущего времени, используемого для пометок.

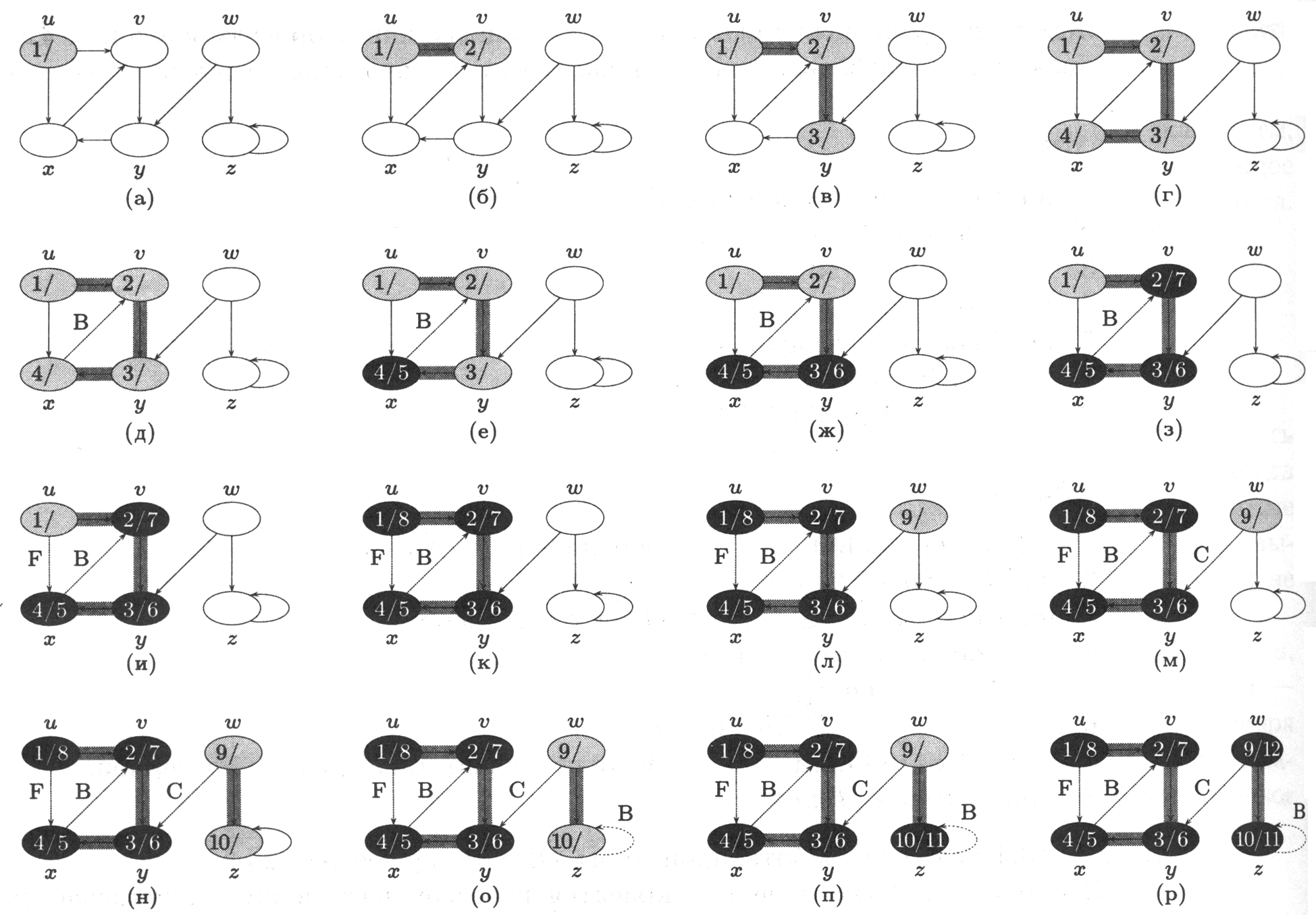
Рисунок 5.2 – Поиск в глубину

На рис. 5.2 показано исполнение алгоритма DFS для ориентированного графа. После просмотра каждое ребро становится либо серым (если оно включается в дерево поиска) или пунктирным (обратные рёбра помечены буквой В (back), перекрёстные – буквой С (cross) прямые – буквой F (forward)). У каждой вершины показаны времена начала и конца обработки.

В строках 1 – 3 (листинг 5.5) все вершины красятся в белый цвет; в поле помещается NIL. В строке 4 устанавливается начальное (нулевое) время. В строках 5-7 вызывается процедура DFS-VISIT для всех вершин (которые остались белыми к моменту вызова – предыдущие вызовы процедуры могли сделать их чёрными). Эти вершины становятся корнями деревьев поиска в глубину.

В момент вызова DFS-VISIT(u) вершина и белая. В строке 1 она ста- новится серой. В строке 2 время её обнаружения заносится в d[u] (до этого счётчик времени увеличивается на 1). В строках 3 – 6 просматриваются смеж- ные с и вершины; процедура DFS-VISIT вызывается для тех из них, которые оказываются белыми к моменту вызова. После просмотра всех смежных с и вершин мы делаем вершину и чёрной и записываем в f [u] время этого события.