Линейная последовательность проб

Пусть h': U  {0,1, ... ,m – 1} – обычная хеш-функция. Функция, определяющая линейную последовательность проб (linear probing), задаётся формулой

h(k, i) = (h'(k) + i) mod т.

Иными словами, при работе с ключом k начинают с ячейки T[h'(k)], а затем перебирают ячейки таблицы подряд: T[h'(k)] + 1],T[h'(k) + 2],... (после Т[т – 1] переходят к Т[0]). Поскольку последовательность проб полностью определяется первой ячейкой, реально используется всего лишь т различных последовательностей.

Открытую адресацию с линейной последовательностью проб легко реализовать, но у этого метода есть один недостаток: он может привести к образованию кластеров, то есть длинных последовательностей занятых ячеек, идущих подряд (по-английски это явление называется primary clustering). Это удлиняет поиск. На самом деле, если в таблице из m ячеек все ячейки с чётными номерами заняты, а ячейки с нечётными номерами свободны, то среднее число проб при поиске элемента, отсутствующего в таблице, есть 1,5. Если, однако, те же m / 2 занятых ячеек идут подряд, то среднее число проб примерно равно m / 8 = n / 4 (п – число занятых мест в таблице). Тенденция к образованию кластеров объясняется просто: если i заполненных ячеек идут подряд, вероятность того, что при очередной вставке в таблицу будет использована ячейка, следующая непосредственно за ними, есть (i + 1) / m, в то время как для свободной ячейки, предшественница которой также свободна, вероятность быть использованной равна всего лишь 1 / m. Всё вышеизложенное показывает, что линейная последовательность проб довольно далека от равномерного хеширования.

Квадратичная последовательность проб

Функция, определяющая квадратичную последовательность проб (quadraty probing), задаётся формулой

h(k, i) = (h’(k)+c₁i + c₂ i) mod m,

где, по-прежнему, h' – обычная хеш-функция, а с₁ и с₂ – некоторые кон­станты. Пробы начинаются с ячейки номер T[h'(k)], как и при линейном ме­тоде, но дальше ячейки просматриваются не подряд: номер пробуемой ячейки квадратично зависит от номера попытки. Этот метод работает значительно лучше, чем линейный, но если мы хотим, чтобы при просмотре хеш-таблицы использовались все ячейки, значения m, с₁ и с₂ нельзя выбирать как попало. Как и при линейном методе, вся последовательность проб определяется своим первым членом, так что опять получается всего т различных перестановок. Тенденции к образованию класте­ров больше нет, но аналогичный эффект проявляется в (более мягкой) форме образования вторичных кластеров (secondary clustering).

Двойное хеширование

Двойное хеширование (double hashing) – один из лучших методов открытой адресации. Перестановки индексов, возникающие при двойном хешировании, обладают многими свойствами, присущими равномерному хешированию. При двойном хешировании функция h имеет вид

h(k,i) = (h₁(k) + ih₂(k)) mod т,

где h₁ и h₂ – обычные хеш-функции. Иными словами, последовательность проб при работе с ключом k представляет собой арифметическую прогрессию (по модулю m с первым членом h₁(k) и шагом ih₂(k).

Чтобы последовательность испробованных мест покрыла всю таблицу, зна­чение h₂(k) должно быть взаимно простым с m (если наибольший общий делитель h₂(k) и m есть d, то арифметическая прогрессия по модулю т с разность h₂(k) займёт долю 1/d в таблице. Простой способ добиться выполнения этого условия – выбрать в качестве m степень двойки, а функцию h₂ взять такую, чтобы она принимала только нечётные значения. Другой вариант: m – простое число, значения h₂ – целые положительные числа, меньшие m. Например, для простого m можно положить

h₁(k) = k mod m,

h₂(k) = 1 + (k mod m'),

где т' чуть меньше, чем m (например, т' = т – 1 или т – 2). Если, например т = 701, т¹ = 700 и k = 123456, то h₁(k) = 80 и h₂(k) = 257. Стало быть, последовательность проб начинается с позиции номер 80 и идёт далее с шагом 257 пока вся таблица не будет просмотрена (или не будет найдено нужное место).

В отличие от линейного и квадратичного методов, при двойном хешировании можно получить (при правильном выборе h₁ и h₂) не m, a (m²) различных перестановок, поскольку каждой паре (h₁(k), h₂(k)) соответствует своя последовательность проб. Благодаря этому производительность двойного хеширования близка к той, что получилась бы при настоящем равномерном хешировании.

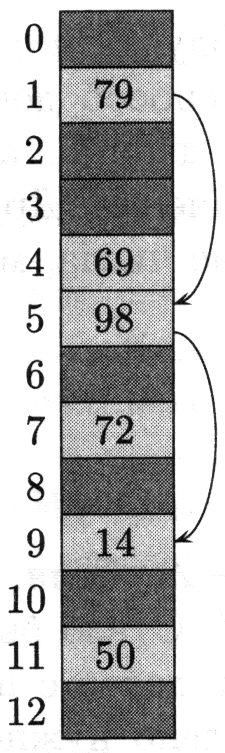
Рисунок 4.6 – Добавление элемента в таблицу с открытой адресацией при двойном хешировании

Рисунку 4.6 соответствует m = 13, h₁(k) = k mod 13, h₂(k) = 1+ (k mod 11). При выбранном k = 14 последовательность проб будет такая: 1-я и 5-я ячейки заняты, 9-я свободна, элемент «14» помещается туда.

Анализ хеширования с открытой адресацией

Так же, как и при анализе хеширования с цепочками, при анализе открытой адресации мы будем оценивать стоимость операций в терминах коэффициент заполнения  = п/т (п – число записей, т – размер таблицы). Поскольку при открытой адресации каждой ячейке соответствует не более одной записи,   1.

Мы будем исходить из предположения о равномерности хеширования этой идеализированной схеме предполагается следующее: мы выбираем ключи случайным образом, причём все m! возможных последовательностей проб равновероятны. Поскольку эта идеализированная схема далека от реальности, доказываемые ниже результаты следует рассматривать не как математические теоремы, описывающие работу реальных алгоритмов открытой адресации, а как эвристические оценки.

Начнём с того, что оценим время на поиск элемента, отсутствующего в таблице.

Теорема 4.5. Математическое ожидание числа проб при поиске в с открытой адресацией отсутствующего в ней элемента не превосходит 1/(1 – ) (хеширование предполагается равномерным, через  < 1 обозначен коэффициент заполнения).

Доказательство. Мы предполагаем, что таблица фиксирована, а искомый элемент выбирается случайно, причём все возможные последовательности проб равновероятны. Нас интересует математическое ожидание числа попыток, необходимых для обнаружения свободной ячейки, то есть сумма

где p_i – вероятность того, что мы встретим ровно i занятых ячеек.

Каждая новая проба выбирается равномерно среди оставшихся не испробованными ячеек; если разрешить пробовать повторно уже испробованные ячейки, то часть проб пропадёт зря и математическое ожидание только увеличится. Но для этого нового варианта мы уже вычисляли математическое ожидание, и оно равно