
- •Министерство образования Российской Федерации
- •Содержание
- •1.2 Скорость роста функций
- •1.3 Анализ алгоритмов; время работы в лучшем, худшем случаях и в среднем
- •1.4 Типы данных, структуры данных и абстрактные типы данных
- •1.5 Динамические множества
- •2 Алгоритмы сортировок
- •2.1 Понятие внутренней и внешней сортировки
- •2.2 Сортировка вставками
- •2.3 Сортировка слиянием
- •2.3.1 Описание алгоритма
- •2.3.2 Анализ времени работы алгоритмов «разделяй и властвуй»
- •2.3.2 Анализ времени работы сортировки слиянием через рекуррентное соотношение
- •2.3.3 Анализ времени работы сортировки слиянием через геометрическую интерпретацию
- •2.4 Пирамидальная сортировка
- •2.4.1 Введение в алгоритм
- •2.4.2 Сохранение основного свойства кучи
- •2.4.3 Построение кучи
- •2.5 Быстрая сортировка
- •2.5.1 Введение в алгоритм
- •2.5.2 Описание
- •2.5.3 Разбиение массива
- •2.5.4 Особенности работы быстрой сортировки
- •2.6 Особенности реализации алгоритмов сортировки; сортировка за линейное время
- •2.6.1 Введение
- •2.6.2 Разрешающее дерево сортировки сравнениями
- •2.7 Цифровая сортировка
- •2.8 Сортировка вычерпыванием
- •2.8.1 Описание алгоритма
- •2.8.2 Вероятностный анализ времени работы сортировки вычерпыванием
- •2.8.3 Анализ времени работы сортировки вычерпыванием через геометрическую интерпретацию
- •2.9 Сортировка подсчетом
- •2.9.1 Описание алгоритма
- •2.9.2 Анализ времени работы
- •3 Элементарные и нелинейные структуры данных
- •3.1 Элементарные структуры: список, стек, очередь, дек
- •3.1.1 Список Линейный однонаправленный список
- •Линейный двунаправленный список
- •Двунаправленный список с фиктивными элементами
- •Циклические списки
- •Циклический однонаправленный список
- •Циклический двунаправленный список
- •3.1.2 Стек
- •3.1.3 Очередь
- •3.1.3 Дек
- •3.2 Нелинейные структуры данных
- •3.2.1 Представление корневых деревьев в эвм
- •Обходы деревьев
- •3.2.2 Двоичные деревья Спецификация двоичных деревьев
- •Реализация
- •Обходы двоичных деревьев
- •3.2.3 Двоичные деревья поиска Основные операции
- •Минимум и максимум
- •Следующий и предыдущий элементы
- •Добавление и удаление
- •Случайные деревья поиска
- •Оптимальные деревья поиска
- •4 Хеширование
- •4.1 Введение
- •4.2 Прямая адресация; таблицы с прямой адресацией
- •4.3 Хеш – таблицы; возникновение коллизий и их разрешение
- •Разрешение коллизий с помощью цепочек
- •Анализ хеширования с цепочками
- •4.4 Способы построения хеш – функций Выбор хорошей хеш-функции
- •Ключи как натуральные числа
- •Деление с остатком
- •Умножение
- •Универсальное хеширование
- •4.5 Открытая адресация; способы вычисления последовательности испробованных мест: линейная последовательность проб, квадратичная последовательность проб, двойное хеширование
- •Линейная последовательность проб
- •1 / (1 – )
- •5 Основные принципы разработки алгоритмов
- •5.1 Введение в теорию графов
- •5.1.1 Графы
- •5.1.2 Представление графов
- •5.2 Алгоритмы на графах: поиск в ширину, поиск в глубину
- •5.2.1 Поиск в ширину (волновой алгоритм)
- •5.2.2 Анализ поиска в ширину
- •5.2.3 Деревья поиска в ширину
- •5.2.4 Поиск в глубину
- •5.2.5 Анализ поиска в глубину
- •5.2.6 Свойства поиска в глубину
- •5.2.7 Классификация рёбер
- •5.3 Топологическая сортировка, задача о разбиении графа на сильно связанные компоненты
- •5.3.1 Топологическая сортировка
- •5.3.2 Сильно связные компоненты
- •5.4 Алгоритм построения минимального остовного дерева
- •5.4.1 Остовные деревья минимальной стоимости
- •5.4.2 Построение минимального покрывающего дерева
- •5.4.3 Алгоритмы Крускала и Пpимa
- •5.4.4 Алгоритм Крускала
- •5.4.5 Алгоритм Прима
- •5.5 Задача нахождения кратчайших путей на графах; алгоритм Флойда; алгоритм Дейкстры
- •5.5.1 Нахождение кратчайшего пути
- •5.5.2 Алгоритм Дейкстры
- •5.5.3 Алгоритм Флойда
- •5.6 Поиск с возвратом
- •5.6.1 Введение
- •5.6.2 Переборные алгоритмы
- •5.6.3 Метод ветвей и границ
- •5.6.4 Метод альфа-бета отсечения
- •5.6.5 Локальные и глобальные оптимальные решения
- •5.7 Метод декомпозиции ( «Разделяй и властвуй»)
- •5.7.1 «Ханойские башни»
- •5.8 Жадные алгоритмы и динамическое программирование
- •5.8.1 Задача о выборе заявок
- •5.8.2 Дискретная задача о рюкзаке
- •5.8.3 Непрерывная задача о рюкзаке
- •5.8.4 Числа Фибоначчи
- •5.8.5 Задача триангуляции многоугольника
- •5.8.6 Дп, жадный алгоритм или что-то другое?
Циклический двунаправленный список
В этом циклическом списке любой элемент имеет два указателя, один из которых указывает на следующий элемент в списке, а второй указывает на предыдущий элемент.
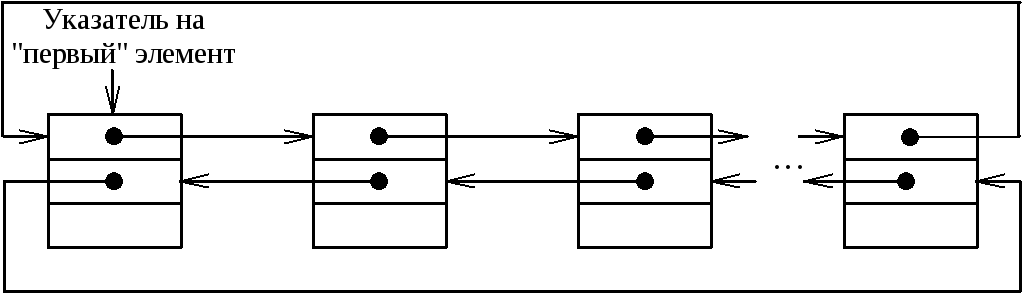
Рисунок 3.5 – Циклический двусвязный список
Основные операции, осуществляемые с циклическим двунаправленным списком:
– вставка элемента;
– просмотр;
– поиск;
– удаление элемента.
Для описания алгоритмов этих основных операций используем те же объявления данных, что и для линейного двунаправленного списка.
Вставка элемента в список, как уже говорилось, проще, чем для линейного двунаправленного списка и реализуется с помощью одной единственной процедуры: Ins_CicleDubleList. В качестве входных параметров передаются: данное для заполнения создаваемого элемента, указатель на начало списка и указатель на текущий элемент в списке, после которого осуществляется вставка. Выходными параметрами процедур является указатель на начало списка (который возможно изменится) и указатель текущего элемента, который показывает на вновь созданный элемент.
procedure Ins_CicleDubleList(DataElem: TypeData;
var ptrHead, ptrCurrent: PElement);
{Вставка элемента в циклический двунаправленный список
справа от элемента, на который указывает ptrCurrent}
var
ptrAddition: PElement; {вспомогательный указатель}
begin
New(ptrAddition);
ptrAddition^.Data := DataElem;
if ptrHead = nil then begin {список пуст}
{создаем первый элемент списка}
ptrAddition^.Next := ptrAddition; {петля из 1 элемента}
ptrAddition^.Last := ptrAddition;
ptrHead := ptrAddition;
end else begin {список не пуст}
{вставляем элемент списка справа от элемента,}
{на который указывает ptrCurrent}
ptrAddition^.Next := ptrCurrent^.Next;
ptrCurrent^.Next := ptrAddition;
ptrAddition^.Last := ptrCurrent;
ptrAddition^.Next^.Last := ptrAddition;
end;
ptrCurrent := ptrAddition;
end;
Листинг 3.14 – Процедура добавления элемента в циклический двусвязный список
Порядок следования операторов присваивания процедуры очень важен. При неправильном переопределении указателей возможен разрыв списка или потери указателя на первый элемент, что приводит к потере доступа к части или всему списку.
Операция просмотра и операция поиска для циклического двунаправленного списка реализуются абсолютно аналогично соответствующим процедурам для циклического однонаправленного списка, и приводить их не будем. Отметим только, что просматривать и искать здесь можно в обоих направлениях.
Операция удаления элемента также осуществляется во многом аналогично удалению из циклического однонаправленного списка.
procedure Del_CicleDubleList(var ptrHead, ptrCurrent: PElement);
{Удаление элемента из циклического двунаправленного списка}
var
ptrAddition: PElement; {дополнительный указатель}
begin
if ptrCurrent <> nil then begin {вх.параметр корректен}
if ptrHead^.Next <> ptrHead then begin
{Если удаляемый элемент не единственный в списке}
ptrAddition := ptrCurrent^.Next;
ptrCurrent^.Last^.Next := ptrCurrent^.Next;
ptrCurrent^.Next^.Last := ptrCurrent^.Last;
if ptrHead = ptrCurrent then {удаляем первый}
ptrHead := ptrCurrent^.Next;
dispose(ptrCurrent);
ptrCurrent := ptrAddition;
end else begin
ptrHead:=nil;
dispose(ptrCurrent);
ptrCurrent:=nil;
end;
end;
end;
Листинг 3.15 – Процедура удаления элемента из циклического двусвязного списка
Использование двух указателей в циклическом двунаправленном списке позволяет ускорить операции, связанные с передвижением по списку за счет двунаправленности этого движения. Однако, элементы списка за счет дополнительного поля занимают больший объем памяти. Операции вставки и удаления элементов здесь осуществляются проще, чем в линейном двунаправленном списке, но сложнее, чем в циклическом однонаправленном списке (за счет необходимости манипулирования большим числом указателей).
