ANSYS Mechanical

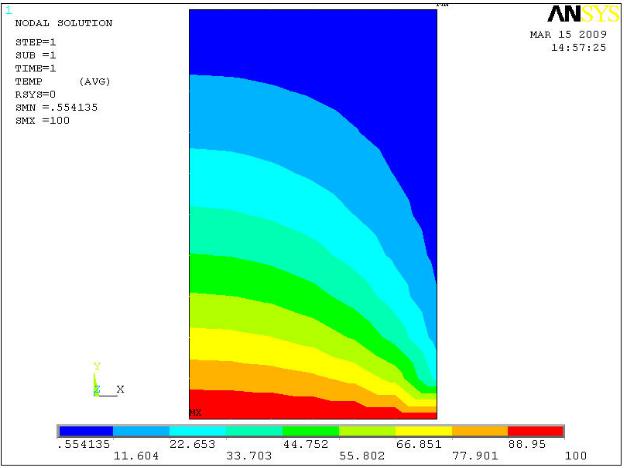
vk.com/club152685050ANSYS Mechanical. |Верификационныйvk.com/id446425943отчет. Том 2 (примеры из Verification Manual)т

Методика расчёта

Задача теплопроводности решается в стационарной постановке. Разложение матрицы жёсткости выполняется с помощью метода SPARSE.

Результаты расчёта

Значения температуры в точке ТР-1, полученные в ходе расчета на разных типах сеток и с применением различных типов элементов, сравниваются с результатом

NAFEMS, Т = 18,3°C.

Рис. 9.8 Визуализация результатов. Распределение температуры, °C. Показанное решение получено при использовании элементов PLANE35, сетка элементов – регулярная треугольная, длина грани элемента N1 = 0,2

vk.com/club152685050ANSYS Mechanical. |Верификационныйvk.com/id446425943отчет. Том 2 (примеры из Verification Manual)т

Таблица 9.1

Сопоставление результатов расчёта.

vk.com/club152685050ANSYS Mechanical. |Верификационныйvk.com/id446425943отчет. Том 2 (примеры из Verification Manual)

Пример 10 (VM2). Статический расчёт шарнирно опертой балки

Постановка задачи

Балка с поперечным сечением A, шарнирно оперта и находиться под действием равномерно распределенной нагрузки w, как показано на рис.10.1. Требуется определить максимальное изгибающее усилие σ и перемещение δ в середине пролета балки.

Рис.10.1 Иллюстрация задачи. Расчетная схема

Физические характеристики

Модуль упругости E = 2,109×107 тс/м2 Коэффициент Пуассона ν = 0,3

Геометрические характеристики

Длина пролета l = 6,096м

Длина консольной части a = 3,048м Высота поперечного сечения h = 0,762 м

Площадь поперечного сечения A = 0,03268 м2

Момент инерции поперечного сечения Iz = 3285,28×10-6 м4

vk.com/club152685050ANSYS Mechanical. |Верификационныйvk.com/id446425943отчет. Том 2 (примеры из Verification Manual)

Описание КЭ-модели

Для решения данной задачи применялся 1 тип КЭ BEAM3 – плоский (двумерный) линейный элемент балки, имеющий 2 узла (по 3 степени свободы в каждом).

Ось КЭ-модели балки располагается вдоль оси X глобальной декартовой системы. Элементы имеют локальную систему координат, ось x’ которой ориентирована вдоль оси элемента, ось y’ располагается в плоскости X-Y, ортогонально оси x’.

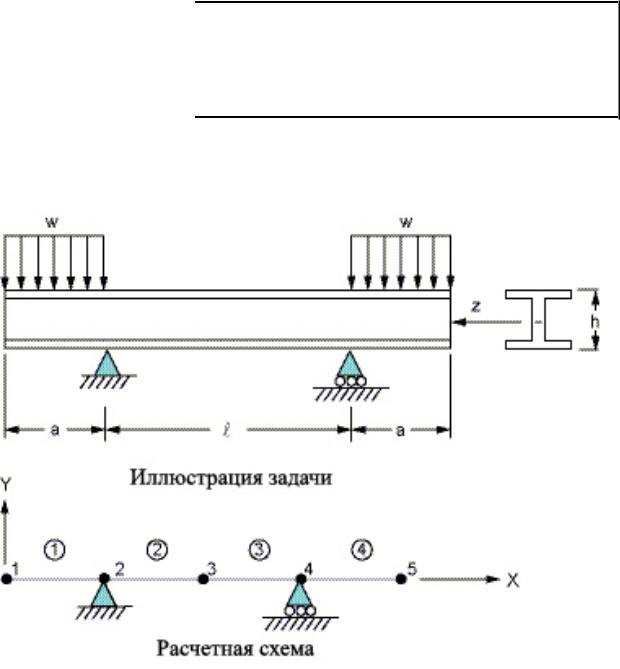
Характерные размеры элементов (длина) составили 3,048 м, таким образом, вычислительная размерность задачи – 5 узлов и 4 КЭ. Число степеней свободы 15.

Граничные условия x = 3,048 м

Ux = 0 Uy = 0

x = 9,144 м Uy = 0

Нагрузки

Равномерно распределенная нагрузка w = 14,888 тс/м; приложена к элементам 1 и 4

Рис.10.2 КЭ-модель балки с указанием закреплений и нумерацией узлов и элементов

vk.com/club152685050ANSYS Mechanical. |Верификационныйvk.com/id446425943отчет. Том 2 (примеры из Verification Manual)

Методика расчёта

Проводится линейный статический расчет. Разложение матрицы жёсткости выполняется с помощью метода SPARSE.

Результаты расчёта

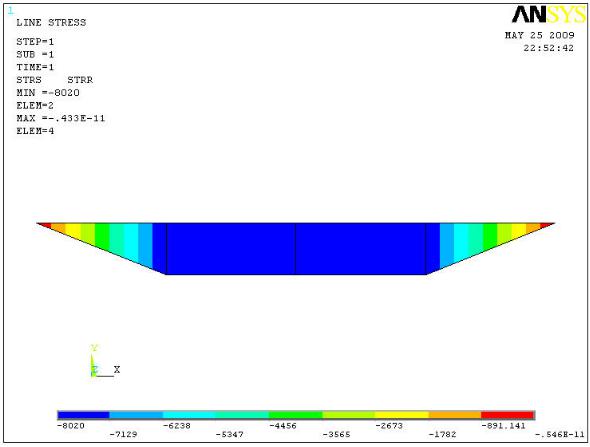
Результатом расчёта являются эпюра изгибных напряжений балки и эпюра перемещений.

Рис.10.3 Эпюра изгибных сжимающих напряжений в балке на нижней грани (тc/м2)

vk.com/club152685050ANSYS Mechanical. |Верификационныйvk.com/id446425943отчет. Том 2 (примеры из Verification Manual)

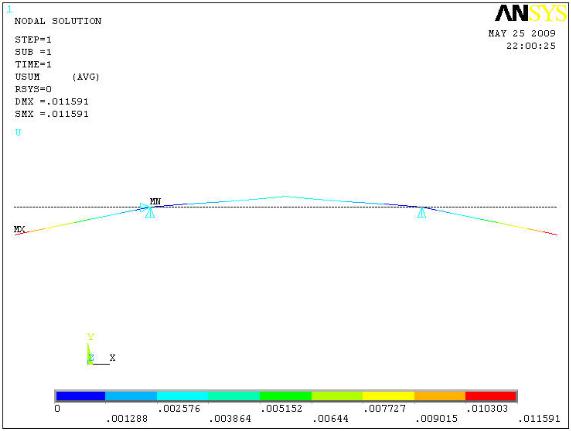
Рис.10.4 Перемещения балки Uy, м

Максимальная по абсолютной величине погрешность δ (расхождение с [Источник]):

– для BEAM3 δ = 0,291%

vk.com/club152685050ANSYS Mechanical. |Верификационныйvk.com/id446425943отчет. Том 2 (примеры из Verification Manual)

Пример 11 (VM6). Цилиндрическая оболочка под действием статических сосредоточенных нагрузок

Постановка задачи

В середине длины тонкостенного цилиндра со свободными краями приложены “навстречу друг другу” 2 сосредоточенные радиальные силы F (“расплющивание” цилиндра).

Требуется определить радиальное перемещение в точке приложения силы.

Рис.11.1 Расчетная схема

Физические характеристики

Модуль упругости E = 7,382 ×106 тс/м2 Коэффициент Пуассона ν = 0, 3125

Геометрические характеристики

Длина l = 0,26289 м Радиус r = 0,12581 м Толщина t = 0,002388 м

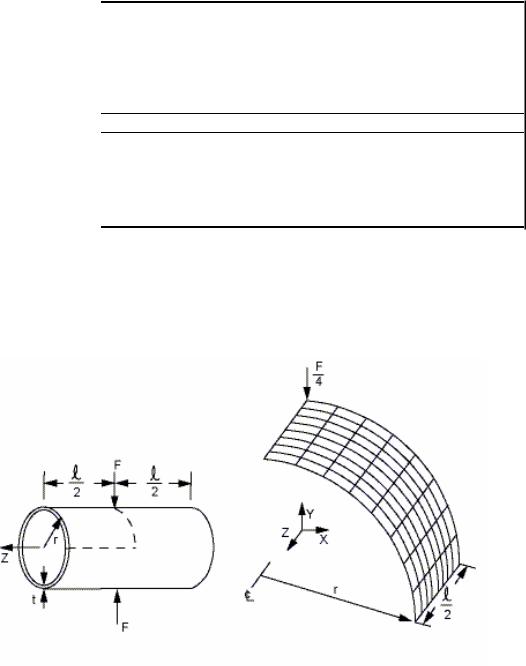
Описание КЭ-модели

Для решения данной задачи применялись 4 типа КЭ:

vk.com/club152685050ANSYS Mechanical. |Верификационныйvk.com/id446425943отчет. Том 2 (примеры из Verification Manual)

SHELL93 – восьмиузловой элемент, обычно используется для моделирования искривленных оболочек. Имеет шесть степеней свободы в каждом узле. Вид перемещений является квадратичным в обоих направлениях в плоскости элемента.

SHELL150 – восьмиузловой p–элемент оболочки с максимальной степенью интерполяционного многочлена, равной восьми. Предназначен для расчёта изгибных оболочек. Имеет шесть степеней свободы в каждом узле.

SHELL181 – оболочечный элемент, имеющий четыре узла. В данном элементе реализована теория оболочек Миндлина-Рейсснера.

SHELL281 – оболочечный восьмиузловой конечный элемент, реализующий теорию оболочек Миндлина-Рейсснера.

В силу симметрии задачи рассматривается одна восьмая часть цилиндра (см. Рис.11.1Расчетная схема). Ось КЭ-модели цилиндра располагается вдоль оси Z глобальной декартовой системы координат.

Характерные размеры элементов, вычислительная размерность задачи (число степеней свободы) и количество узлов и элементов отображены в следующей таблице:

Граничные условия

По краям 1/8 части цилиндра в силу симметрии задачи наложены граничные условия симметрии.

При x = 0:

Ux = 0 Roty = 0 Rotz = 0

При y = 0:

Uy = 0 Rotx = 0 Rotz = 0

При z = 0:

Uz = 0 Rotx = 0 Roty = 0

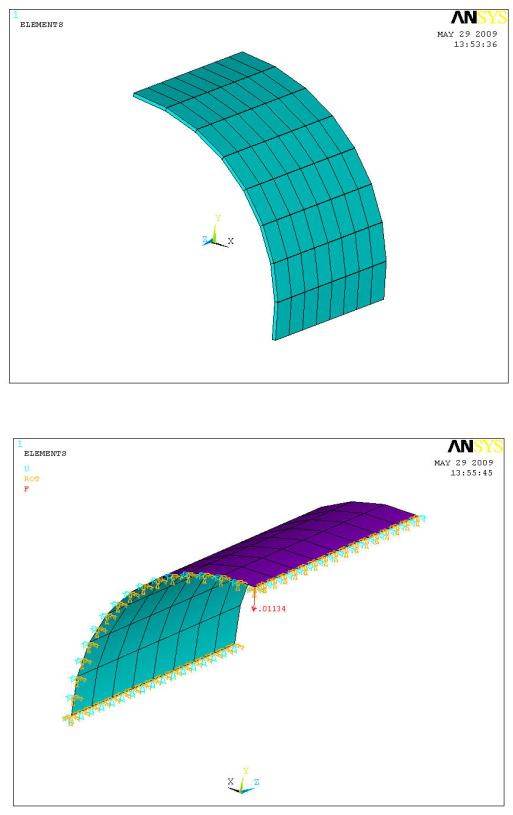
Нагрузка

В силу симметрии задачи прикладывается четверть радиальной силы в узел цилиндра с координатами (0; 0,125806; 0):

Fy = 0,01134 тс

vk.com/club152685050ANSYS Mechanical. |Верификационныйvk.com/id446425943отчет. Том 2 (примеры из Verification Manual)

Рис.11.2 Изометрия КЭ-модели цилиндра. 3D-визуализация

Рис.11.3 Изометрия КЭ-модели цилиндра с указанием закреплений и нагрузки

vk.com/club152685050ANSYS Mechanical. |Верификационныйvk.com/id446425943отчет. Том 2 (примеры из Verification Manual)

Методика расчёта

Проводится линейный статический расчет. Разложение матрицы жёсткости выполняется с помощью метода SPARSE.

Результаты расчёта

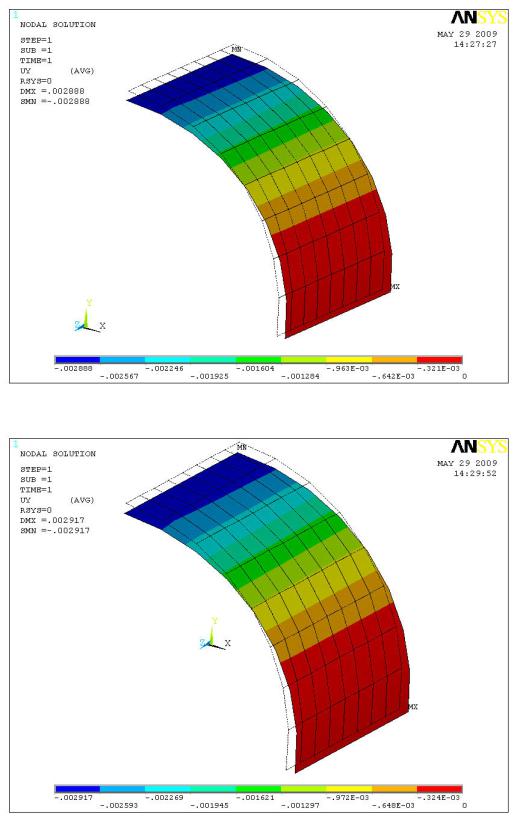
Результатом расчёта являются перемещения. Ниже приведено сравнение результатов по ANSYS и данных [Источник].

Рис.11.4 Радиальные перемещения Uy, м и деформированное состояние (SHELL93)

Рис.11.5 Радиальные перемещения Uy, м и деформированное состояние (SHELL150)