
- •1. Гидростатика
- •1.1. Вводные сведения. Свойства и параметры состояния жидкости
- •1.1.1 Гидромеханика как наука
- •1.1.2 Свойства и параметры состояния жидкости
- •1.2 Основные законы и уравнения статики
- •1.2.1 Силы, действующие в жидкости
- •1.2.2 Гидростатическое давление
- •1.2.3 Дифференциальные уравнения покоя жидкости
- •1.2.4 Интегрирование уравнения Эйлера
- •1.2.5. Основное уравнение гидростатики
- •1.2.7 Пьезометрическая высота
- •1.2.8 Сила гидростатического давления
- •1.2.9. Закон Архимеда
- •2. Динамика идеальных и реальных жидкостей
- •2.1. Кинематика потенциальных и вихревых потоков
- •2.1.1. Гидромеханика упругой невязкой жидкости
- •2.1.2. Струйная модель жидкости
- •1.2.3. Виды движения жидкости
- •1.2.4. Гидравлические элементы потока
- •1.2.5. Уравнение неразрывности и постоянства расхода жидкости
- •2.2. Основные законы и уравнения динамики жидкости
- •2.2.1. Уравнение движения Эйлера
- •2.2.2. Уравнение Бернулли для элементарной струйки идеальной жидкости
- •2.2.3. Геометрический и физический (энергетический) смысл уравнения Бернулли
- •2.2.4. Уравнение Бернулли для целого потока вязкой жидкости
- •2.3. Моделирование гидравлических процессов. Элементы теории размерностей
- •2.3.1. Основные понятия о подобии гидравлических явлений
- •2.3.2. Критерии динамического подобия
- •2.3.3. Пи – теорема
- •2.4. Взаимодействие тел с потоком жидкости
- •2.4.1. Гидравлическое уравнение количества движения
- •2.4.2. Сила действия движущейся жидкости на твердые тела
- •2.4.3. Гидравлическая крупность
- •3. Движение напорных потоков вязкой жидкости
- •3.1. Режимы движения жидкости
- •3.1.2. Основные закономерности при ламинарном движении жидкости
- •3.2. Гидравлические сопротивления
- •3.2.1. Гидравлические сопротивления по длине
- •3.2.2. Местные гидравлические сопротивления
- •3.3. Гидравлический расчет трубопроводных систем
- •3.3.1. Расчет длинных простых трубопроводов
- •3.3.2. Расчет коротких трубопроводов
- •3.3.3. Расчет сложного трубопровода
- •4. Безнапорные и свободные потоки жидкости
- •4.1. Равномерное движение в открытых руслах
- •4.2. Неравномерное безнапорное установившееся движение воды в каналах
- •5. Основы теории фильтрации
- •5.1. Закон Дарси
- •5.1.1. Основные понятия и определения
- •5.1.2. Коэффициент фильтрации
- •5.2. Равномерное движение грунтовой воды
- •5.3. Напорное движение фильтрационного потока
- •5.4. Безнапорные фильтрационные потоки
- •Список литературы
- •Геометрическая интерпретация уравнения Бернулли для целого потока реальной жидкости – диаграмма Бернулли.
- •Геометрическая интерпретация уравнения Бернулли
- •Энергетическая интерпретация уравнения Бернулли
- •Уравнение Бернулли для потока идеальной жидкости
- •График Никурадзе
- •-Типы потоков жидкости
- •-Гидравлические характеристики потока жидкости
- •Уравнение гидравлического прыжка в руслах прямоугольного сечения. Потери энергии в прыжке
- •Классификация водосливов
- •Основная формула расхода через водослив
- •Истечение через водослив с тонкой стенкой
- •Возможные схемы и режимы сопряжения бьефов
- •Донный режим сопряжения
- •Состав грунта
- •Пористость грунтов
- •Скорость фильтрации. Основной закон ламинарной фильтрации (формула Дарси)
- •ФОРМУЛА ДЮПЮИ
vk.com/club152685050 | vk.com/id446425943
13
PM = dz dy |
( p − ∂p |
dx) |
(1.24) |
|
на грань 3-4 |
|
dx |
2 |
|
∂p |
dx) |
|
|
|
PN = dz dy ( p + |
|
(1.25) |
||
|
dx |
2 |
|
|
в) на грани 2-3 и 1-4 все силы будут проектироваться в «0» |
||||
2. Составляем уравнение: |
∂p |
dx) |
|
∂p dx) = 0 (1.26) |
ρ Фхdxdy dz + dzdy( p − |
− dzdy( p + |
|||
|
dx |
2 |
|
dx 2 |
Разделим (1.26) на dy, dz и приведем подобные:
ρ Фхdx + p − 12 ∂dxp dx − p − 12 ∂dxp dx = 0,
ρ Фхdx − ∂dxp dx = 0.
Рассуждая аналогично и рассматривая равновесие всех сил на оси OY и OZ, получим уравнения равновесия для покоящейся жидкости (уравнения Эйлера):
Фх − ρ1 ∂dxp = 0
Фy − |
1 ∂p |
= 0 |
(1.27) |
||
|
|
||||
ρ dy |
|||||
|
|
|
|||
Фz − ρ1 ∂dzp = 0
1.2.4Интегрирование уравнения Эйлера
Умножая первое уравнение (1.27) на dx, второе на dy,третье на dz и складывая их, получим:
Φx dx + Φy dy + Φz dz − |
1 |
∂p |
dx + |
∂p |
dy + |
∂p |
dz)= 0 |
|
|
|
∂x |
∂y |
∂z |
||||
|
||||||||
|
ρ |
|
|
|
||||
Выражение вскопках является полным дифференциалом функции р, поэтому можно написать:
dp = ρ(Φx dx + Φy dy + Φz dz) |
(1.28) |
Если жидкость однородна и несжимаема, то ρ =const и правая часть уравнения есть полный дифференциал некоторой функции П, называемой потенциальной энергией массовых сил:
|
∂Π |
∂Π |
|
∂Π |
|
|||
Φx = |
|
; Φy = |
|
; |
Φz = |
|
; |
|
∂x |
∂y |
∂z |
|
|||||
тогда (1.28) dp=ρdП. |
p=ρП + C. |
|
|
|
|
|
|
|
Интегрируя, получим: |
|
|
|
|
|
|
||
Для определения С рассмотрим точку с известными р=р0 |
и П=П0 |
|||||||
p0=ρП0 + C → C=p0 – ρП0 |
→ p=p0 + ρ(П-П0). (1.29) |
|||||||

vk.com/club152685050 | vk.com/id446425943
14
1.2.5. Основное уравнение гидростатики
Рассмотрим жидкость, заключенную в неподвижном сосуде и находящуюся в поле действия силы тяжести. Примем Oz –направлена вверх.
Φx=0; Φy=0; Φz=-g.
Подставим эти данные (1.28) dp=-ρgdz.
Проинтегрируем это выражение в пределах: от р0 до р и от z0 до z при ус-
ловии ρ=const
p |
z |
p – p0 = ρgh |
∫∂p = ∫− ρgdz; |
||
p0 |
z0 |
|
p = p0 |
+ρgh |
(1.30) |
где: р– абсолютное давление в данной точке; ро– абсолютное давление окру- |
||
жающей среды (внешнее давление); ρgh - давление, которое оказывает столб жидкости высотой h.
Выражение (1.30) называется «основное уравнение гидростатики». Оно выражает зависимость давления р в данной точке покоящейся жидкости от рода жидкости ρ, расстояния этой точки от свободной поверхности h и давления на свободной поверхности ро.
Следствия:
1.В покоящейся однородной жидкости любая горизонтальная плоскость является плоскостью равного давления.
2.Внешнее давление, оказываемое на жидкость, заключенную в замкнутом сосуде, передается ею во все точки без изменения (принцип Паскаля). На нем основано действие гидравлических прессов, домкратов и т.д.
1.2.6.Виды и способы измерения гидростатического давле-
ния
Гидростатическое давление можно измерить относительно абсолютного нуля и тогда такое давление будет именоваться абсолютным, и относительно

vk.com/club152685050 | vk.com/id446425943
15
другого какого-либо давления и тогда оно будет называться относительным. Абсолютный нуль давления возможен, если объем (пространство) вообще лишено какого-либо вещества, например, полный вакуум в космическом пространстве, либо при полной остановке движения молекул (при абсолютном нуле температуры).
На поверхности земли относительно абсолютного нуля давления измеряется преимущественно только атмосферное давление и для этого используются различные барометры (жидкостные, механические). Все остальные способы измерения гидростатического давления осуществляются относительно атмосферного давления.
Допустим, что на свободную поверхность жидкости действует атмосфер-
ное давление т.е. ро=ра , то р=ра + ρgh. |
|
|
1. |
Если р > pa, то разность |
|
|
р – ра =рм |
(1.31) |
называется манометрическим давлением. Манометрическое давление это |
||
превышение абсолютного давления в данной точке над атмосферным. |
|
|
2. |
Если абсолютное давление в точке жидкости меньше атмосферного |
|
давления р < pa , то разность |
|
|
|
ра – р = рв |
(1.32) |
называется вакуумом. Вакуум – это недостаток давления в данной точке
до атмосферного. Величина вакуума изменяется в пределах 0 < pв< pa . Соотношение между абсолютным, манометрическим и вакуумметриче-
ским давлениями иллюстрирует следующая схема.
1.2.7Пьезометрическая высота
1.Рассмотрим закрытый резервуар не полностью заполненный жидкостью давление, на свободной поверхности которого больше атмосферного. Подключим к т. А тонкую открытую стеклянную трубку – пьезометр. Благодаря действию давления в т. А жидкость в трубке поднимется на некоторую
высоту hизб. Со стороны жидкости в сосуде давление в т. А равно рА.
Со стороны жидкости в трубке давление в т. А равно
vk.com/club152685050 | vk.com/id446425943
16
Так как давления в т. А слева и справа равны можно записать
Высота hизб называется пьезометрической высотой.
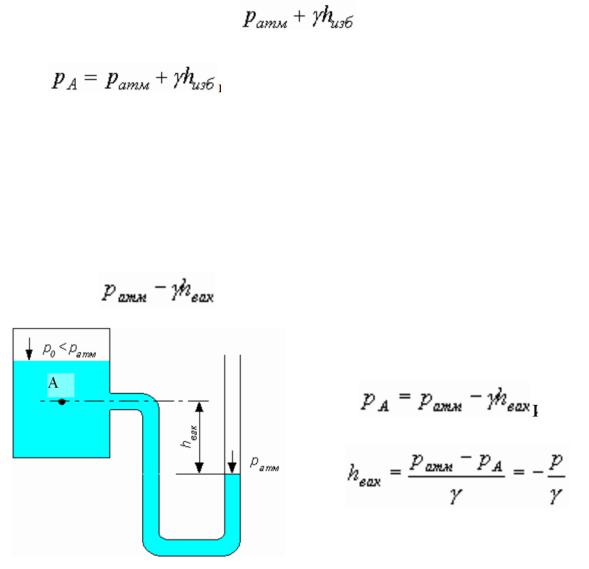
2. Рассмотрим закрытый резервуар не полностью заполненный жидкостью давление, на свободной поверхности которого меньше атмосферного. Подключим к т. А U-образный пьезометр. Очевидно этом случае уровень жидкости в пьезометре опустится ниже уровня жидкости в резервуаре Со стороны жидкости в сосуде давление в т. А равно рА.
Со стороны жидкости в трубке давление в т. А равно
Так как давления в т. А слева и справа равны можно записать
или
Высота hвак называется вакуумметрической высотой. Вакуумметрическая высота характеризует разность атмосфер-
ного и абсолютного давлений. Именно эта разность, а не само давление называется вакуумом. Вакуум в данной точке есть недостаток давления до атмосферного.
1.2.8Сила гидростатического давления
Вобщем случае воздействия жидкости на твердую поверхность (S) сводится к сумме элементарных сил dP, действующих на малые площадки dω, составляющих эту поверхность.
Если n – единичный вектор нормали к поверхности ω, а р – давление на площадке dω, то сила
r |
(1.33) |
dP = pndω |
Суммируя систему сил dP, получаем выражение для главного вектора силы давления
r |
|
P = ∫pndω |
(1.34) |
ω
выражение для главного момента

vk.com/club152685050 | vk.com/id446425943
17
r |
|
L = ∫ω r × pndω , |
(1.35) |
где r – радиус-вектор площадки dω относительно центра приведения системы сил.
Рассмотрим несколько частных случаев.
Случай 1. Равномерное давление действует на плоскую стенку (например: действие капельной жидкости на горизонтальное дно или действие покоящегося газа на стенки сосуда).
В этом случае p = const, n = const и из (1.44) имеем
r |
(1.36) |
P = pnω |
Величина силы Р при равномерном распределении давления не зависит от ориентации плоской стенки ω в пространстве и вычисляется по формуле:
P = pω . |
|
(1.37) |
pа |
pа |
pа |
|
|
h |
S |
S |
S |
Например, для всех резервуаров, представленных на схеме, давление на дне будет равно p = p0+ρgh, а сила
P = ( p0 + ρgh)ω0 , |
(1.38) |

vk.com/club152685050 | vk.com/id446425943
18
т.е. сила давления на дно не зависит от формы сосуда (гидростатический парадокс).
Случай 2. Сила равномерного давления на криволинейную стенку (p = const; n ≠ const ). Например, действие покоящегося газа на криволинейные стенки сосуда:
В этом случае элементарные силы dP имеют разные направления. Главный P вектор системы вычисляется через свои проекции. Чтобы найти его про-
екции, например Рх, проектируем на ось Х векторы r
dP = pndω
|
r |
(1.39) |
|
dPx = pdωX 0 n = p cos(n; x)dω = pdωx |
|
где X0 |
=единичный вектор оси Х; dωx – проекция площадки dω на плоскость |
|
нормальную к оси Х. |
|
|
Искомая величина Рх при p = const |
|
|
|
Px = ∫p cos(n, x)dω = p ∫dωx = pωx |
(1.40) |
ωωx
Из (1.40) следует, что линия действия Рх проходит через центр тяжести площади проекции ωх.
S
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dP = pdSn |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х0 |
|
|
dSx |
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dS |
|
|
|
|
||
|
|
Аналогично можно определить: |
и |
Pz = Pωz . |
(1.41) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Py = Pωy |
||||||||
Если три проекции на три взаимно ортогональные оси пересекаются в од-
ной точке, то система сил dP может быть сведена только к силе давления, величина которого равна:
|
P = |
|
Px |
2 + Py |
2 + Pz |
2 |
, |
(1.42) |
||||
а направление определяется направляющими косинусами |
|
|||||||||||
|
cos(P, x) = |
Px |
|
; |
|
|
|
|||||
|
P |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos(P, y) = |
Py |
; |
|
|
(1.43) |
||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
cos(P, z) = |
|
Pz |
. |
|
|
|
|||||
Случай 3. |
|
P |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
Сила |
неравномерного давления на |
плоскую стенку |
||||||||||
r |
Например, давление жидкости на плоскую вертикальную |
|||||||||||
(P ≠ const; n = const) . |
||||||||||||
или наклоненную стенку.

vk.com/club152685050 | vk.com/id446425943
19
Систему элементарных сил dP , одинаковых по направлению, но разных по величине, можно свести к одной силе давления.
r |
(1.44) |
P = n∫ pdω . |
|
ω |
|
Величина этой силы |
(1.45) |
P = ∫pdω |
|
ω |
|
зависит от закона распределения давления р по площади ω.
Вычислим силу Р для плоской стенки ОМ, наклоненной к горизонту под углом α. В плоскости этой стенки наметим оси координат ОУ и ОХ. Ось ОХ направим перпендикулярно к плоскости чертежа, а ОУ – по стенке ОМ.
На стенке сосуда ОМ наметим некоторую плоскую фигуру любого очертания, имеющую площадь ω. Эта фигура на плоскость чертежа будет проектироваться в линию (показано на чертеже жирно).
Развернем плоскость УОХ на 900 и совместим с плоскостью чертежа. Теперь намеченная плоская фигура будет изображаться без искажения.
Поставим перед собой задачу, во-первых, найти величину силы давления Ра и, во-вторых, найти положение линии действия силы Ра .
Наметим на плоской фигуре точку m имеющую координаты y и x. Из рис. видно, что
y sinα = h . |
(1.56) |
У точки m выделим элементарную площадку dω. Сила гидростатического давления на эту площадку
dP = pdω = ρghdω = ρgysin dω |
(1.57) |
Интегрируя по всей площади ω, получим:

vk.com/club152685050 | vk.com/id446425943
20
P = ρg sinα∫ydω |
(1.58) |
ω |
|
Интеграл ∫ydω представляет собой статический момент площади ω отно-
ω
сительно оси ОХ, равный, как известно, произведению ω на координату yc ее центра тяжести. Поэтому
P = ρg sinα ycω = ρghcω , |
(1.59) |
или |
|
P = pcω , |
(1.60) |
где hc – глубина заглубления центра тяжести площадки ω; рс – гидростатическое давление в центре тяжести площадки ω.
Согласно (1.60) величина силы гидростатического давления на плоскую стенку равна произведению площади стенки на давление в ее центре тяжести.
Точка D пересечения линии действия силы Р с плоскостью рассматриваемой фигуры называется центром давления. Для отыскания координат этой точки (Xd;Yd) используем теорему о равенстве момента равнодействующей и суммы моментов составляющих, которая в данном случае выражается уравнением:
r |
r |
r |
(1.61) |
rd × P = ∫r |
×npdω |
||
s
где rd и r – радиус – векторы соответственно центра давления D и произвольной точки m (x;y) площади ω.
Откуда
|
∫y2dω |
|
|
|
∫xyds |
|
|
|
||
Yd = |
ω |
|
и |
Xd |
= |
ω |
. |
|
|
(1.62) |
|
|
|
|
|||||||
y ω |
y ω |
|
|
|||||||
|
c |
|
|
|
c |
|
|
|
|
|
Случай 4. Неравномерное |
давление |
на |
криволинейную |
поверхность. |
||||||
r |
|
|
|
|
r |
имеют разные величи- |
||||
( p ≠ const;n ≠ const) . В этом случае элементарные силы |
dP |
|||||||||
ны и разные направления. Поэтому главный вектор системы |
r |
|
||||||||
P , как и во втором |
||||||||||
случае, вычисляется через свои проекции.
Допустим, надо определить силу гидростатического давления на криво-
линейную поверхность АВ. |
|
dωx |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
X |
|
|
|
|
|
||||
|
|
|
z |
|
A |
dωz dω |
|
|
α |
|
dPx |
|||||
|
|
|
|
|
|
|
||||||||||
|
|
|
||||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
α |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dP |
|||
|
|
|
|
|
|
dP |
|
dPz |
|
|
|
|
|
|
||
|
|
|
B |
|
|
|
|
|
|
|
||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|||
Выделим на этой поверхности элементарную площадку dω. Разложим си- |
||||||||||||||||
лу гидростатического давления на эту площадку dP на составляющие dPx и dPz.
Величины этих составляющих будут равны |
|
dPx=ρgzdωz |
(1.63) |
