3. Розрахунок параметрів тарілчастого туковисіваючого апарату

Технологічний процес роботи тарілчастого туковисіваючого апарату включає 2 фази: виведення шару добрив через регульоване вікно та скидання їх з тарілки.

Секундне виведення добрив тарілкою з банки залежить від площі вікна та середньої колової швидкості туків

,

де - щільність (об’ємна маса) добрив, кг/м³;

Оскільки

,

Рис. 7.2. Схема виведення добрив тарілкою туковисівного апарату: 1-тарілка; 2-банка

;

де - висота вікна, м.

То отримаємо

.

А виходячи з умови забезпечення необхідної дози внесення туків маємо

,

де - норма внесення туків, кг/га;

- робоча ширина захвату машини, м;

- поступальна швидкість машини, м/с;

- кількість висівальних апаратів.

Прирівнявши праві частини виразів, отримаємо

.

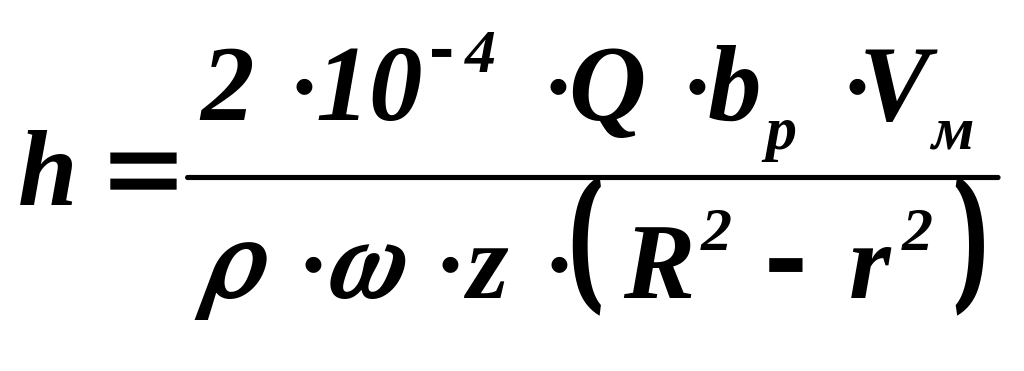4. Теорія дискового відцентрового розкидача

Робочий процес відцентрового висіваючого апарату складається з 2 фаз: відносне переміщення частинок добрив по диску і падіння туків кинутих диском у горизонтальній площині.

Для визначення мінімальної необхідної частоти обертання диска, при якій спостерігається рух частинки по диску, розглянемо плоский диск із розташованою на ньому частинкою туків.

На частинку діють: сила тертя та відцентрова сила переносного руху (рис. 7.3, а), а умова рівноваги частинки матиме вигляд

.

Рис. 7.3. Схема до розрахунку параметрів дискового відцентрового розкидаючого апарату

Або

.

Якщо рахувати, що - мінімальному радіусу падіння туків із кузова, а , то отримаємо

.

Таким чином, за частоти обертання розкидаючого диска розрахованою за формулою (7.16) ще можливий рух частинки добрив по ньому.

Частинка, яка впала на диск, через певний проміжок часу зустрінеться із лопаткою і далі продовжить свій рух вздовж неї. При цьому на частику добрив діють: відцентрова сила інерції , яку можна розкласти на складову направлену вздовж лопатки та перпендикулярно до неї ; коріолісова сила інерції , яка діє у напрямку протилежному до напрямку коріолісового прискорення; сили тертя по диску та по лопатці . Тоді умова рівноваги матиме вигляд

.

Або

.

Якщо врахувати, що при граничних умовах та , то отримаємо

.

Звідки отримаємо

.

Таким повинен бути мінімальний радіус падіння частинок туків, для забезпечення їх руху вздовж лопатки.

Після досягнення частинкою краю лопатки відбувається її кидок та вільний політ. У цей момент абсолютна швидкість частики становить

.

Але оскільки , то можна прийняти, що , тобто швидкості переносного руху частинки із диском.

Без урахування опору повітря політ частинки може бути описаний системою

де - час польоту частинки.

Із другого рівняння системи маємо при

,

де - висота встановлення розкидальних дисків над поверхнею поля, м

З урахуванням отриманого із першого рівняння системи (7.21) отримаємо

,

де - віддаль польоту частинки, м.

Використовуючи отриманий вираз можна записати залежність для визначення ширини захвату дводискового апарату

,

де - віддаль між центрами дисків, .

В існуючих машинах м; ; м/с; , де - поступальна швидкість машини.