8.2.5.2 Подключение r -цепи к источнику постоянного напряжения

1. Запишем правило коммутации для цепи на рис. 8.8

.

2. Получим дифференциальное уравнение цепи

,

+

, ,

. Рис.8.8

Характеристическое уравнение цепи , корень которого .

Постоянная времени .

3. Запишем полное решение .

Здесь свободная составляющая также включает только одну экспоненту, поскольку цепь имеет первый порядок.

4. Подставив в полное решение t = 0⁺, определим постоянную интегрирования на основании правил коммутации .

Т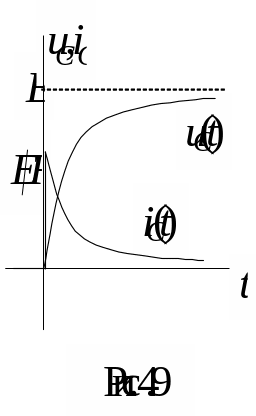 аким образом, окончательный результат имеет вид

.

Ток в цепи

. Рис. 8.9

Графики изменения и представлены на рис. 8.9. Значение тока, содержащее лишь свободную составляющую, максимально в начальный момент времени, когда оно скачком достигает значение , и все напряжение источника приложено к резистору. По мере зарядки конденсатора напряжение на нем повышается, что ведет к соответственному уменьшению тока в цепи.

4.2.5.3 Подключение rl-цепи к источнику постоянного напряжения

1. Запишем правило коммутации для цепи на рис. 8.10

.

2. Получим дифференциальное уравнение цепи

,

,

характеристическое уравнение

.

Рис. 8.10 Корень характеристического уравнения и постоянная времени соответственно

, .

3. Полное решение имеет вид: .

4. Подставив в i_L(t) t = 0⁺ на основании правила коммутации определим постоянную интегрирования .

Т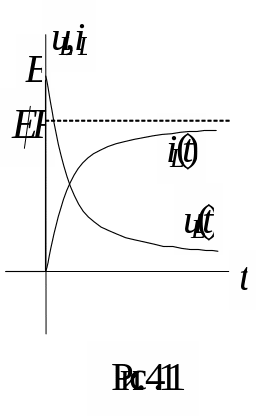 аким образом, .

Напряжение на индуктивности

. Графики изменения u_L(t), i_L(t) приведены на рис. 8.11.

Рис. 8.11

8.2.5.4 Подключение rc-цепи к источнику гармонического напряжения

Рассмотрим случай, когда в цепи (рис. 8.12) действует источник синусоидальной ЭДС

.

З десь – фаза включения, т.к. она определяется моментом срабатывания коммутатора. Интуитивно следует ожидать влияние на качественную и количественную картину протекания переходного процесса.

Порядок расчета переходных процессов, описанный выше, не претерпевает никаких изменений. Рис.8.12

1. Запишем правило коммутации .

2. Дифференциальное уравнение и соответствующее ему характеристическое уравнение:

.

Корень характеристического уравнения .

3. Полное решение для рассматриваемой цепи первого порядка

.

4. Расчет принужденной составляющей произведем символическим методом

;

;

;

.

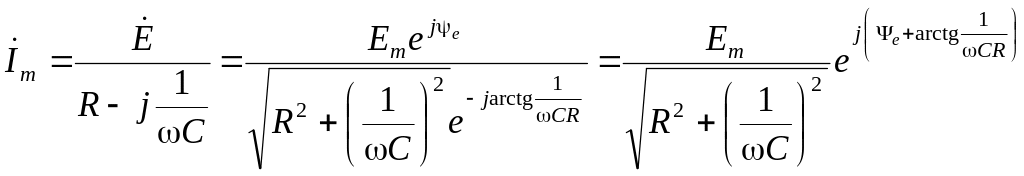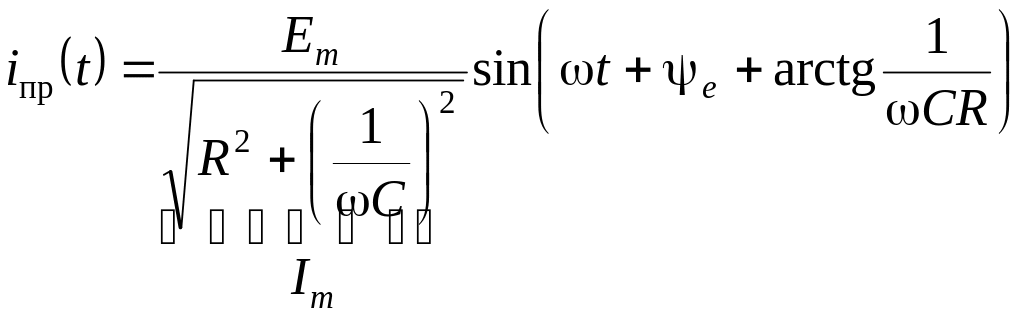5. Для расчета постоянной интегрирования запишем полное решение для момента t = 0⁺

;

.

В соответствии с правилом коммутации ;

Таким образом,

или

.

Определим

;

Оба выражения для u_C и i_C в общем случае имеют периодическую принужденную и апериодическую свободную составляющие. При этом характер переходного процесса существенно зависит от двух факторов – начальной фазы напряжения источника в момент включения и соотношения параметров цепи и R.

Исследуем ожидаемое влияние фазы включения источника на переходный режим

1) Пусть , тогда . Поскольку cos 0 = 1, получим

.

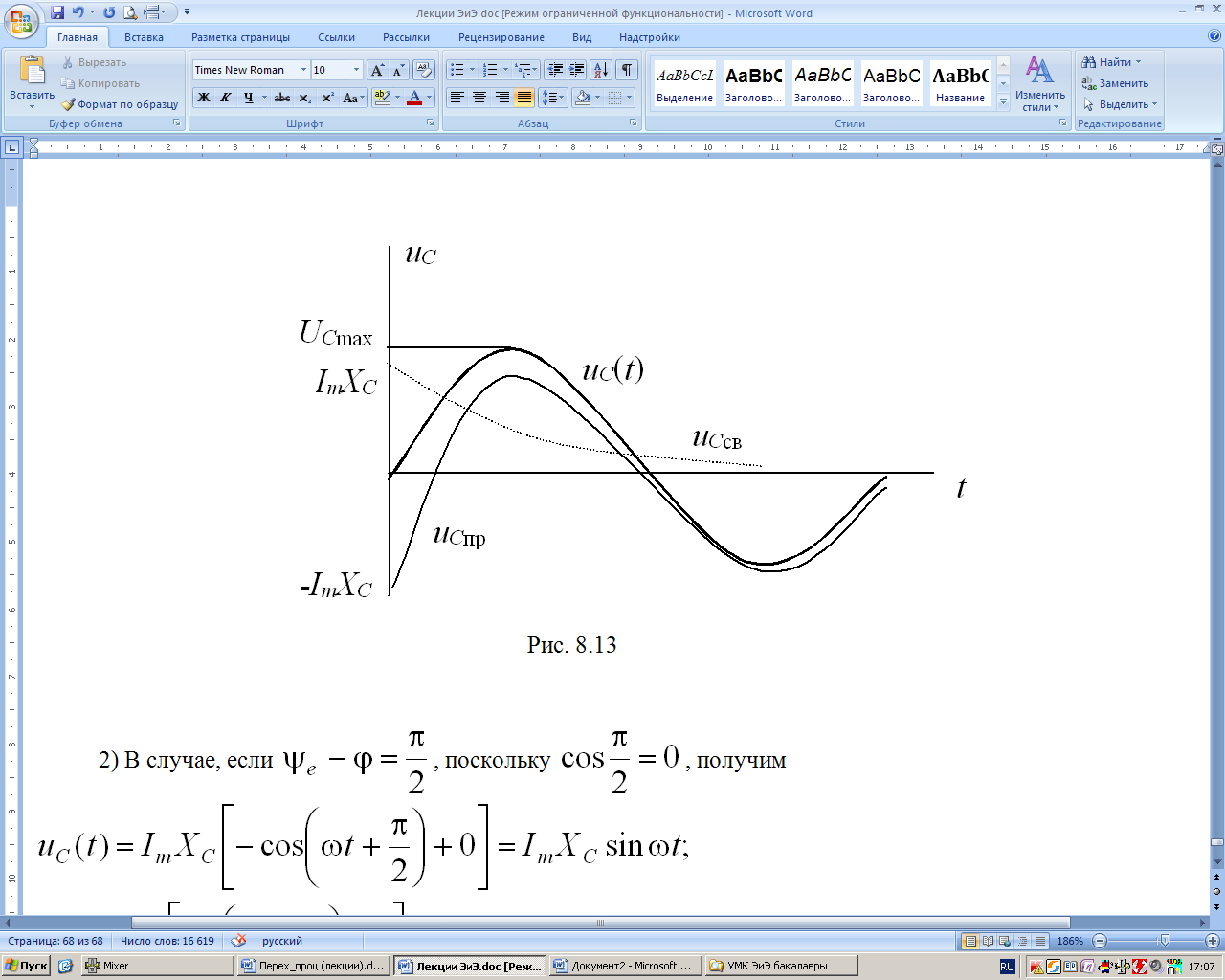
а) исследование кривой напряжения (рис. 8.13) наглядно демонстрирует, что максимальное напряжение в переходном режиме ограничено .

б) исследование кривой тока (рис. 8.14).

Максимальное значение тока в переходном режиме зависит от соотношения Х_С и R и может превышать I_mпр в несколько раз. Однако этот начальный всплеск тока является кратковременным.

2) В случае, если , поскольку , получим

Т аким образом, в данном случае в цепи переходный процесс не наблюдается.

Рис. 8.14