4.5. Типовые распределения вероятностей

Рассмотрим важнейшие свойства тех законов распределения вероятностей, которые чаще всего используются в математической статистике для проверки гипотез и в других приложениях.

4.5.1. ²-распределение Пирсона (хи-квадрат).

Def. Пусть имеем набор независимых нормально распределенных случайных величин _i с параметрами а = 0,  = 1. Тогда скалярная случайная величина имеет распределение Пирсона с n степенями свободы (n – параметр распределения). Будем обозначать это ²(n).

4.5.2. t-распределение Стьюдента и F-распределение Фишера

Def. Пусть ХN(0, 1) и Y_n²(n) – независимые СВ. Тогда СВ

Имеет t-распределение Стьюдента с n степенями свободы.

Def. Пусть Х_n²(n) и Y_m²(m) – независимые СВ. Тогда СВ имеет F-распределение Фишера с n и m степенями свободы.

Рассмотрим два приложения t- и F-распределений к проверке статистических гипотез.

1. Пусть имеем выборку Х₁, …, Х_N, Х_j  N(a, ²). Тогда СВ имеет t-распределение Стьюдента с N – 1 степенями свободы.

Это означает, что если СВ Х распределена нормально, то статистика Т может быть использована в качестве статистического критерия проверки гипотезы вида Н₀: M[X] = a, где а – заданное число, причем знание  не требуется.

Пример. Масса Х пачки печенья должна быть равна 200 г. Выборочное взвешивание 25 пачек дало следующие оценки = 196.64 г, s² = 36 г². Выдерживается ли заданный вес пачки?

Решение. Выдвигаем гипотезу Н₀: M[X] = 200. = –2.8. При  = 0.05 получаем V_КР = (– , –Т_КР), где Т_КР = СТЬЮДРАСПОБР(0,05; 24) = 2,06. Значит Т_ВЫЧ V_КР и гипотеза не верна, на фабрике не выдерживают необходимые параметры.

2. Пусть имеем две выборки: Х₁, …, Х_n; Х_j  N(a₁, ) и Y₁, …, Y_m; Y_i  N(a₂, ). Пусть , . Тогда СВ имеет F-распределение с n – 1 и m – 1 степенями свободы. В частности, при такое же распределение имеет СВ .

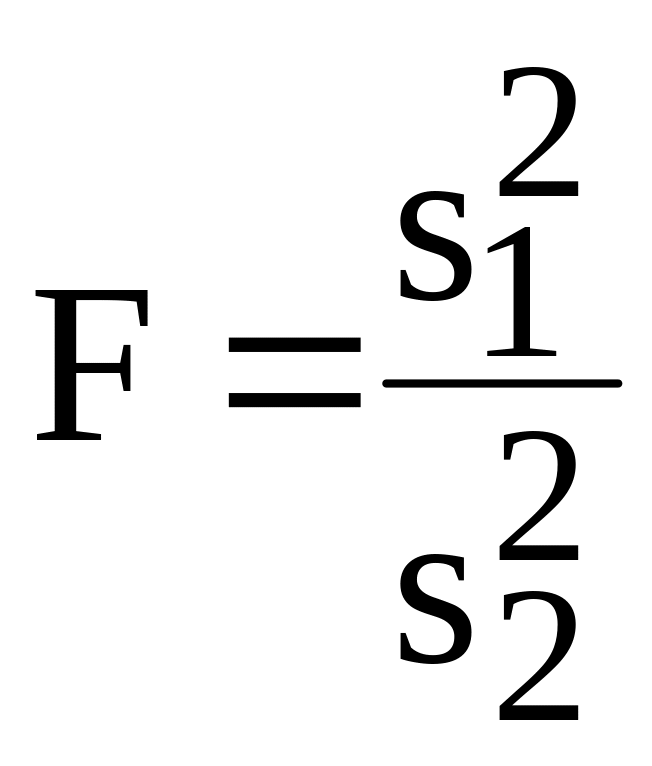Таким образом СВ F можно использовать в качестве статистического критерия проверки гипотезы с критической областью ( FРАСПОБР(1 – ; n –1; m – 1); + ).

4.6. Регрессионный анализ: исследование свойств уравнения регрессии

Остаточная дисперсия

Def. Остаточной дисперсией уравнения регрессии называется величина

,

равная среднему квадрату отклонения экспериментальных данных от расчетных (k – число коэффициентов модели (4.1)).

Величина остаточной дисперсии позволяет оценить точность построенного уравнения. Из нескольких альтернативных вариантов модели при прочих равных условиях предпочтение следует отдавать уравнению, имеющему наименьшую остаточную дисперсию.

Методы, рассматриваемые далее, основаны на следующем допущении: экспериментальные ошибки независимы и распределены нормально.

Проверка значимости МНК-оценок

Def. Если b_j = 0, то говорят, что МНК-оценка незначима.

Это означает, что член b_j f_j (x) не должен входить в модель (4.1).

Выдвинем гипотезу Н₀: b_j = 0. Можно доказать, что при допущении о нормальности экспериментальных ошибок при верной Н₀ случайные величины

, j = 1, …, k, (4.4)

где = (Ф^TФ)^–1 , а – диагональный элемент этой матрицы (см. формулу (4.3)), имеют распределение Стьюдента с числом степеней свободы  = N – k. Критическая область имеет двухстороннюю структуру: если > Т^КРИТ, где Т^КРИТ = СТЬЮДРАСПОБР(; N – k ), то гипотеза не верна и МНК-оценка значима.

Проверка эффективности регрессии. Пусть модель (4.1) содержит свободный член b₀. Тогда имеет место формула

(у_i – )² = (у_i – ) ² +  ²  Q_ОБЩ = Q_ОСТАТ + Q_РЕГР.

Предположим, что влияние на выходной параметр у контролируемых входных параметров х_i незначимо на фоне случайных помех. Этот факт можно сформулировать в виде статистической гипотезы Н₀: b_j = 0  j  0. В отличие от предыдущего пункта, речь идет не об отдельных членах модели, а об уравнении в целом.

Def. Если гипотеза Н₀ верна, то будем говорить, что модель (4.1) неэффективна.

Теорема. Если ошибки эксперимента независимы и распределены нормально, то при верной гипотезе о неэффективности модели (4.1) статистики Q_ОСТАТ /² и Q_РЕГР /² независимы и распределены по законам ²(N – k) и ² (k – 1), соответственно.

Это означает, что при верной гипотезе Н₀: b_j = 0  j 0 статистика

(4.5)

имеет распределение Фишера с числами степеней свободы k – 1 и N – k. Таким образом, для проверки эффективности модели (4.1) может быть использован статистический критерий (4.5) с правосторонней критической областью: если F^ВЫЧ > FРАСПОБР(1 – ; k –1; N – k) = F^КРИТ, то гипотеза не верна и модель (4.1) эффективна.

Пример. Пусть объект характеризуется двумя входными параметрами х1 и х2. Имеем матрицу Х значений входных параметров и вектор у значений выхода:

; .

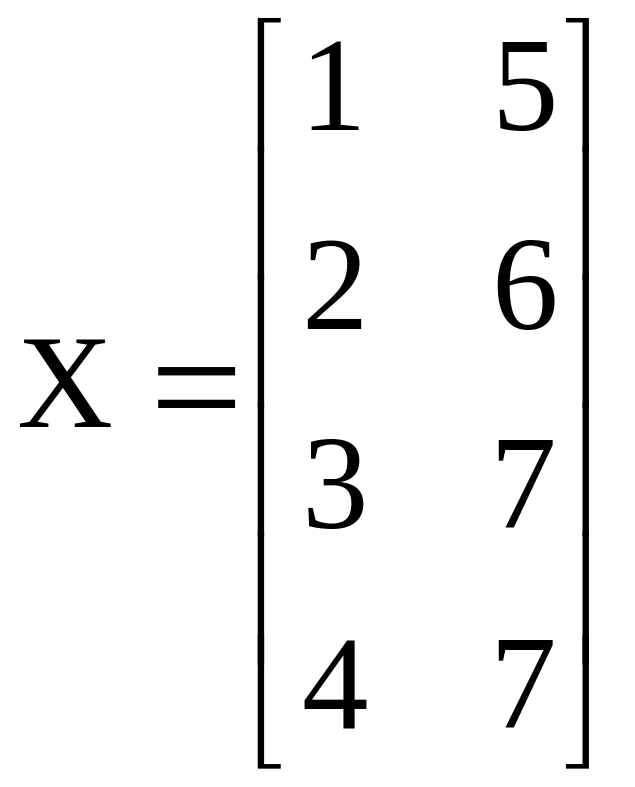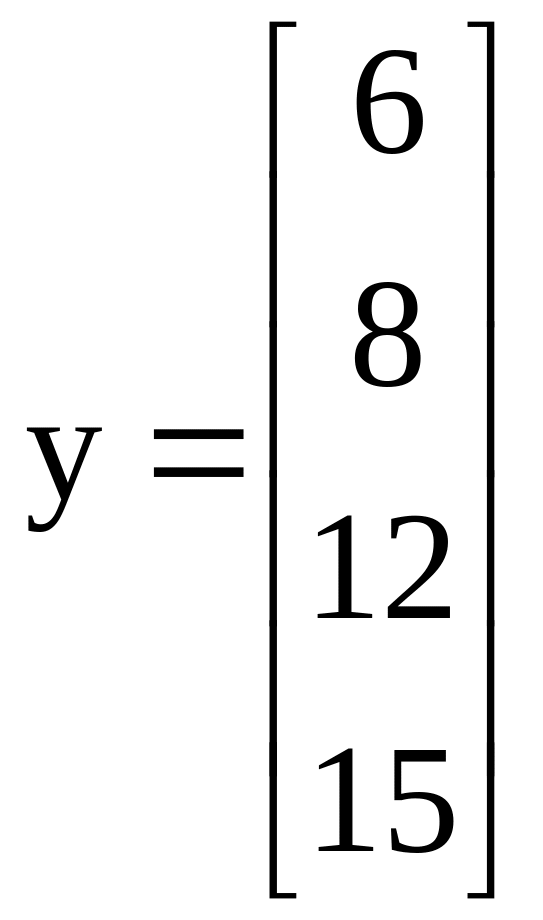Построим по этим данным линейное уравнение регрессии у = b₀ + b₁ x1 + b₂ x2.

Для этого запишем регрессионную матрицу и матрицы, связанные с ней:

; ; .

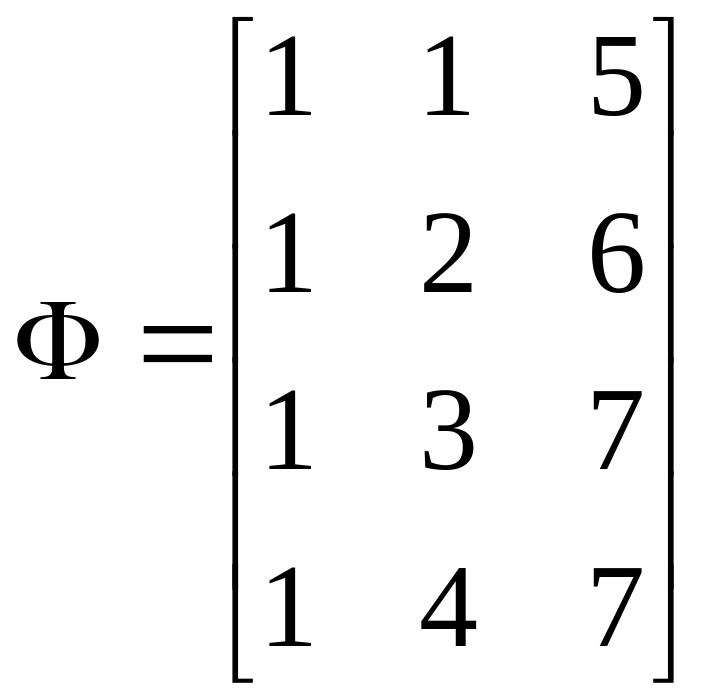В результате решения системы вида (4.2):

,

получаем вектор МНК-оценок, а с его помощью найдем вектор расчетных значений у: ; .

Отсюда Q_ОСТАТ = 0.667; Q_ОБЩ = 48.75; Q_РЕГР = 48.083. Проверим эффективность модели. F^ВЫЧ = 36.06, при  = 0.05 будет F^КРИТ = 199.5. Следовательно, модель неэффективна.

Оценим значимость коэффициентов. Для этого определим оценку дисперсионной матрицы С:

.

Отсюда имеем вектор значений критерия Стьюдента для МНК-оценок

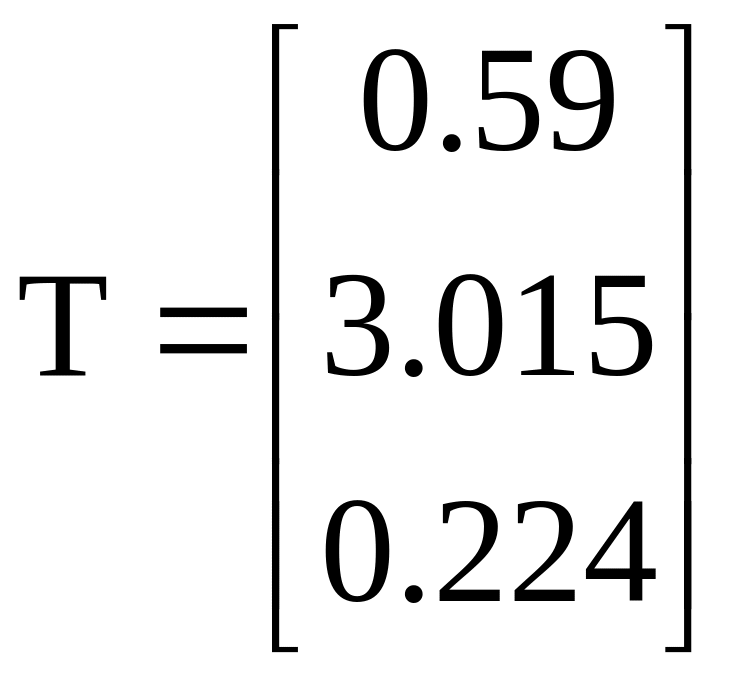при Т^КРИТ = 12.706. Следовательно, все коэффициенты незначимы, модель получилась «нехорошей».

Исключим из уравнения член с минимальным значением |Т_j|, т.е. b₂ x2. Получим модель у =2.5 + 3.1 х1, которая является эффективной: F^ВЫЧ = 137.3, F^КРИТ = 18.5. Новые значения критерия Стьюдента равны (3.45; 11.72) при Т^КРИТ = 4.3. Следовательно, коэффициент при х1 значим, а свободный член “близок к значимому”. Получили приемлемую модель.