4.1.3. Основные понятия математической статистики

Задача математической статистики состоит в разработке методов сбора и обработки статистических данных для получения научных и практических выводов.

Пусть  – некоторая случайная величина (СВ).

Def. Выборкой величины  объема N называют набор из N независимых СВ ₁, … _N, распределенных также, как .

Иными словами, выборка – это N независимых экземпляров СВ .

Def. Статистика – это некоторая функция выборки ( ₁, … _N).

Поскольку статистика зависит от набора случайных величин, то она сама является случайной величиной, а значит, имеет числовые характеристики, такие как математическое ожидание, дисперсия и др.

Def. Пусть  – некоторый параметр СВ , а  – область его значений (). Точечной статистической оценкой параметра  называется любая статистика = (  ₁, …  _N), принимающая значения из области .

Основное назначение статистических оценок – давать приближенное значение для оцениваемого параметра, найденное по реализации выборки. Для того, чтобы это приближение было “хорошим”, статистические оценки должны обладать определенными свойствами.

Пусть – статистическая оценка параметра . Допустим, что по некоторой реализации выборки получено ее числовое значение . Повторяя опыты, т.е. получая другие реализации выборки, мы сможем определить другие значения – , которые, вообще говоря, между собой различны. Следовательно, статистическую оценку надо рассматривать как случайную величину, имеющую определенный закон распределения и числовые параметры – математическое ожидание, дисперсию и т.д. (Этого следовало ожидать, т.к. оценка представляет собой некоторую функцию случайных величин – элементов выборки).

Представим себе, что некоторая оценка постоянно дает значение параметра с избытком. Ясно, что в этом случае и математическое ожидание такой оценки (как случайной величины) будет больше истинного значения параметра. Использование такой оценки привело бы к систематическим (одного знака) ошибкам. Поэтому естественно потребовать, чтобы математическое ожидание статистической оценки было равно истинному значению оцениваемого параметра, т.е. .

Def. Статистическая оценка, математическое ожидание которой равно истинному значению оцениваемого параметра, называется несмещенной.

Примеры статистических оценок. Рассмотрим несколько важных примеров статистических оценок.

1. Оценка = (₁ + … + _N) / N ( среднее) – оценка математического ожидания.

Свойства .

а) M[ ] = M[], т.е. она является несмещённой.

б) D[ ] = D[] / N.

2. Оценка – оценка дисперсии.

Свойства s². Оценка s² является несмещенной. (Можно доказать, что если бы делили на N, то получили бы смещённую оценку).

4.2. Метод моментов вычисления статистических оценок

Для таких “популярных” параметров случайных величин как математическое ожидание и дисперсия найдены явные формулы статистических оценок – и s², соответственно. Однако часто необходимы оценки и других параметров. Например, в теории массового обслуживания часто используется так называемое гамма-распределение, формула плотности которого имеет вид:

,

где ,  – параметры, оценки которых надо найти для идентификации закона распределения; – гамма-функция Эйлера. Для оценок  и , а также многих других параметров специальных формул не разработано. Следовательно, необходимы методы поиска оценок для произвольных параметров. Одним из наиболее простых является метод моментов (Пирсона).

Def. Теоретическим начальным моментом k-го порядка СВ  называется величина

.

Например, математическое ожидание – начальный момент 1-го порядка.

Def. Теоретическим центральным моментом k-го порядка СВ  называется величина

.

Например, дисперсия – центральный момент 2-го порядка, центральный момент 1-го порядка любой СВ равен 0.

Def. Эмпирическим начальным моментом k-го порядка СВ  называется величина

.

Def. Эмпирическим центральным моментом k-го порядка СВ  называется величина

.

При больших N эмпирические моменты можно приравнять к теоретическим. На основании таких равенств составляется система уравнений для оценок параметров СВ, если есть выражения искомых параметров через теоретические моменты. На этом и основан метод моментов. Его главное достоинство – простота. Кроме того, не нужно знания закона распределения СВ. Единственное требование – большой объем выборки.

Пример. Методом моментов найдем параметры гамма-распределения  и . Известны следующие формулы:

.

Подставляем вместо теоретических моментов эмпирические – получаем систему уравнений относительно оценок  и :

.

Поделим первое уравнение на второ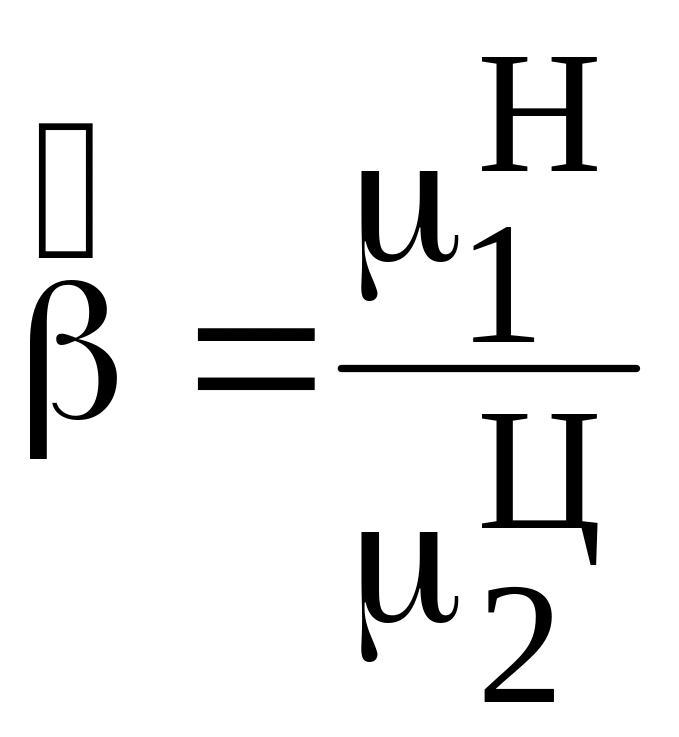е – получим ; подставим в 1-е уравнение – получим .