4.3. Регрессионный анализ: синтез уравнения регрессии

Таблица 4.1.
xi	–3	–2.5	–2	–1.5	–1	–0.5
yi	–1.92	–1.45	–0.57	0.62	0.88	2.03

Пример. Имеются экспериментальные данные (Таблица 4.1). Построить функцию, отражающую зависимость у от х, т.е её аппроксимацию. (приближение).

Если нанести точки на график и соединить их, то получим зигзагообразную линию, которая, впрочем, не слишком отличается от прямой (см. рис. 3.1). Поэтому аппроксимирующую функцию будем искать в классе многочленов первой степени, т.е. положим Y(x) = b₁ x + b₂. Для идентификации (нахождения) этой зависимости надо найти статистические оценки коэффициентов модели. Согласно методу наименьших квадратов (МНК) эти оценки находят из условия минимума функции

.

В данном случае на искомые коэффициенты не наложено никаких ограничений, т.е. мы имеем классическую задачу минимизации функции нескольких переменных – b₁ и b₂. Из курса математики известно, что для минимизации таких функций надо вычислить частные производные минимизируемой функции, приравнять их к 0 и решить полученные уравнения.

Рис. 4.1. График данных примера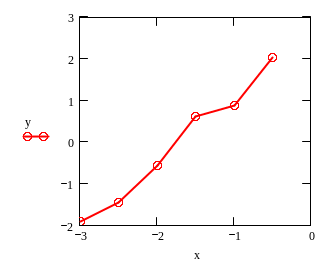

Имеем:

Раскроем скобки, разобьем каждое выражение на несколько сумм и перенесем члены, зависящие от искомых коэффициентов налево, а независящие – направо.

Подставим данные из таблицы 4.1 – получим линейную систему относительно искомых коэффициентов:

Решив систему, получим b₁ = 1.596; b₂ = 2.725, а аппроксимирующая функция примет вид Y(x) = 1.596 x + 2.725. На рис. 3.2 приведены графики исходных данных (точки) и аппроксимирующей функции (сплошная линия).

Рис. 4.2. Графики исходных данных и аппроксимирующей функции

Описанный метод нахождения коэффициентов основан на минимизации функции Q(b ₁, b ₂ ), представляющую собой сумму квадратов. Поэтому он называется методом наименьших квадратов (МНК).

Матричная запись МНК. В более общем случае будем искать уравнение регрессии в виде функции, линейно зависящей от коэффициентов, т.е.

у = b₁ f₁(x) + … + b_k f_k(x), (4.1)

где f_u(x) – заданные функции; b_u – неизвестные коэффициенты. Для идентификации этой зависимости надо найти статистические оценки коэффициентов модели. Согласно методу наименьших квадратов (МНК) эти оценки находят из условия минимума функции

Q(b) = ,

где у_i – наблюдаемое значение выходного параметра в i-м эксперименте.

Обозначим: Ф = [Ф_ij] = [f_j(xⁱ)] – регрессионная (N  k)-матрица; b – вектор коэффициентов; у – вектор значений выхода. Тогда для вектора оценок коэффициентов имеем уравнение

(Ф^T Ф) = Ф^T y. (4.2)

Значит

= (Ф^T Ф)^–1 Ф^T y. (4.3)

4.4. Проверка статистических гипотез

Def. Статистическая гипотеза – некое суждение о свойствах случайной величины. Проверка статистической гипотезы – процедура сопоставления выбранной гипотезы с имеющимися экспериментальными данными, сопровождаемая количественной оценкой степени достоверности полученного вывода.

Пример 4.1. Согласно паспортным данным автомобильного двигателя, расход топлива на 100 км должен составить 10 л. Испытано 25 машин. Средний расход топлива составил = 9.3 л. Известно, что расход топлива – СВ Х с известной дисперсией ² = 4 л². Проверить гипотезу: m_x = 10 л.

Обозначим Н₀ – выдвигаемая гипотеза. Идея проверки состоит в вычислении по результатам эксперимента некоторой статистики К = К(Х₁, …, Х_N) – статистического критерия, обладающего следующим свойством: если гипотеза Н₀ верна, то случайная величина К имеет строго определенный закон распределения. Чтобы проверить, справедлив ли в действительности этот закон, вся область V значений критерия разбивается на две части: V_КР – критическая область (область отклонения гипотезы) и V \V_КР – область принятия гипотезы. Если в результате эксперимента событие (K  V_КР) не выполнится, то гипотезу следует принять. В противном случае ее надо отвергнуть Для построения критической области введем понятия ошибок I и II рода.

Def. Ошибка I рода состоит в отклонении верной гипотезы. Ошибка II рода состоит в принятии неверной гипотезы.

Чтобы понять разницу между этими понятиями – обратимся к примеру.

Пример. Система ПВО засекла летящий самолет. Гипотеза Н₀ – самолет вражеский. В данном примере ошибка I рода состоит в том, что при верной гипотезе она была отвергнута, и вражеский самолет пропустили на свою территорию. Ошибка II рода – гипотеза была неверна, но ее приняли, в результате чего был сбит свой самолет. Приведенный пример, в частности демонстрирует, что, как правило, цена ошибок I и II рода различна.

В принятых обозначениях P_I = P(KV_КР / Н₀) =  – вероятность ошибки I рода; P_II = P(KV \V_КР /  Н₀) =  – вероятность ошибки II рода. (Символ  Н₀ означает, что  Н₀ не верна, наклонная черта / означает «при условии», а всё выражение (KV \V_КР /  Н₀) читается так: К принадлежит области V \V_КР при условии, что Н₀ не верна.

Принцип выбора V_КР: при заданном уровне P_I =  вероятность ошибки II рода должна быть минимальна (  min или 1–  mах).

Величина  называется уровнем значимости, она равна максимально допустимому значению вероятности ошибки I рода. В технических задачах обычно полагают  = 0,05. Величина 1 –  называется доверительной вероятностью.

Законы распределения статистических критериев могут быть различны. В настоящее время для всех употребляемых законов разработаны специальные методы построения критических областей. Их границы определяются по статистическим таблицам, а при использовании программ статистического моделирования применяются встроенные функции. Например, если критерий распределён нормально, то в Excel используется функция НОРМОБР(р; а; ), где р – заданная доверительная вероятность, а и  – параметры нормального распределения (см. Примеры основных законов распределения непрерывных СВ).

Проверим гипотезу примера 4.1 при  = 0.05. В качестве статистического критерия примем . При нормальном распределении СВ Х с параметрами m_x = 10, D[X] = ² выбранный критерий К распределен нормально с параметрами m_К = 0, D[K] = 1. Тогда критическая область имеет вид:

V_КР = (– ; НОРМОБР(1– ; 0 ; 1)) = (– , – 1.645).

Расчетное значение критерия К^ВЫЧ при = 9.3 л составит К^ВЫЧ = – 1.75 , т.е. попадает в критическую область (– , – 1.645). Следовательно, основная гипотеза должна быть отвергнута.

Резюме: технология проверки статистических гипотез

1. Проводится серия экспериментов для получения статистического материала.

2. По полученным данным выдвигается статистическая гипотеза.

3. Задаётся уровень значимости , определяется тип выдвинутой гипотезы и соответствующий статистический критерий К. По виду гипотезы и значению  определяется критическая область V_КР.

4. По экспериментальным данным вычисляется значение К^ВЫЧ.

5. Если К^ВЫЧ попадает в V_КР, то основная гипотеза отвергается, в противном случае – принимается.