§ 6. Передаточные функции линейных систем.

Рассмотрим линейную систему, находящегося под влиянием задающего g(t) и возмущающегоf(t) воздействий (рис 6.1)

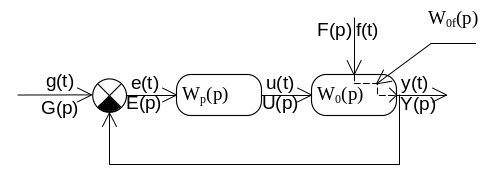
Передаточная ф – ия регулятора:

ПФ - ия объекта по регулирующему воздействию:

ПФ - ия объекта по возмущающему воздействию:

Операторное уравнение динамики объекта:

(1)

С учетом 1 структурная схема 6.1 м.б. представлена в виде (рис 6.2)

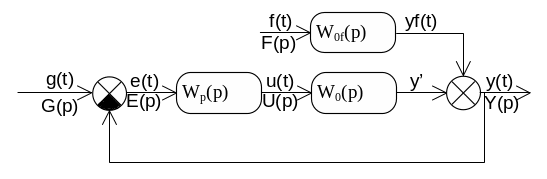
Если разорвать главную обратную связь F(o)=0, то получим ПФ - ию разомкнутой…

При этом структурная схема ( рис 6.2) упрощается (рис 6.3)

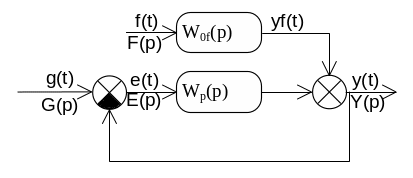
Если разорвать главную ОС, то при , то получим ПФ - ию разомкнутой системы по возмущающему воздействию:

Рассмотрим теперь замкнутую систему.

При Ф(p)

Учитываю что

Ф(p)

N(p)- характеристический полином разомкнутой системы; D(p)- характеристический полином замкнутой системы.

При G(p)=0 получим ПФ – ию замкнутой системы по ошибке от возмущающего воздействия

Ф(p)

Рассмотрим возможные ПФ - ии замкнутой системы. На основе схемы (рис. 6.3) составим сигнальный граф, где отобразим параметры системы .

Рисунок 6.4

При , получим ПФ - ию замкнутой системы. Из рисунка 6.3 и алгебры обратного соединения получаем, что

Учитывая, что , получим:

, где

N(p) - характеристический полином разомкнутой системы; Д(p) - характеристический полином замкнутой системы.

При , получим ПФ-ию замкнутой системы по ошибке от возмущающего воздействия:

.

По формуле Мезона имеем:

.

По полученным ПФ-ям можно записать операторное уравнение относительно регулируемой величины:

.

Если в качестве выходной величины рассматривать сигнал ошибки , а в качестве входной - сигнал задающего воздействия , то, полагая , получим передаточную функцию замкнутой системы по ошибке от задающего воздействия.

Из рисунка 6.4 следует:

; ;

.

Найдем связь между и :

.

Учитывая, что возмущение также влияет на отклонение регулируемой величины, а, следовательно, и на сигнал ошибки, то, полагая , получим ПФ - ию замкнутой (?) по ошибке от возмущающего воздействия:

.

Из рисунка 6.4:

; ;

.

Таким образом, регулирующая ошибка системы имеет две составляющие:

.

§7 Временные характеристики линейных звеньев

В реальных условиях входные сигналы имеют произвольный характер. Для исследования динамических свойств звеньев (систем) следует выбирать такие типовые сигналы, которые по возможности наиболее близко отражали бы наиболее существенные особенности реальных сигналов. Кроме того, для сравнения отдельных элементов и систем между собой их также следует подвергать однотипным воздействиям. К числу наиболее часто применяемых типовых сигналов относятся:

- единичная ступенчатая функция 1(t);

- единичная импульсная функция ;

- гармоническая функция .

Временной характеристикой звена (системы) по какому-либо внешнему воздействию называют закон изменения выходной величины звена при изменении внешнего воздействия по определенному закону и при условии, что до приложения внешнего воздействия звено находилось в покое (нулевые начальные условия).

1. Реакцию звена на воздействия в виде единичной ступенчатой функции при нулевых начальных условиях называют переходной функцией (рис. 7.1).

Графическое изображение переходной функции называют переходной характеристикой.

x

t

0

1

h(t)

t

x(t)=1(t)

Рисунок 7.1

Единичная ступенчатая функция определяется следующими условиями:

.

Согласно определению ПФ - ии изображение выходного сигнала:

.

Учитывая, что

,

.

2. Реакция звена на воздействие в виде единичной импульсной функции при нулевых начальных условиях называется весовой или импульсной переходной функцией (рис 7.2).

Графическое изображение функции называется импульсной переходной характеристикой.

x(t)

t

-δ(t)

ω(t)

t

0

Рисунок 7.2

Единичная импульсная функция или дельта-функция представляет собой импульс бесконечно большой амплитуды и бесконечно малой длительности (рис. 7.2а).

;

Математически дельта - функцию можно представить как производную от единичной ступенчатой функции:

,

отсюда следует

Таким образом, площадь импульса имеет конечную величину, равную единице.

и являются математической абстракцией реально существующих сигналов.

При экспериментальном исследовании систем за -функцию принимают всякое кратковременное ударное воздействие с продолжительностью , которая значительно меньше длительности переходного процесса. В этом случае амплитуда импульса будет . При таком подходе можно трактовать как предел прямоугольного импульса (рис. 7.3), у которого амплитуда стремится к бесконечности, а время его действия :

δ(t)

S=1

t

Δt→0

Рисунок 7.3

.

Учитывая, что входной сигнал или ,

Переходная и импульсная связаны соотношением:

или

Если момент приложения импульсной функции к звену принять за начало отсчета, равное (рис. 7.4), то при или .

x(t)

δ(t-τ)

τ

t

y (t)

τ

-ω(t-τ)

t

Рисунок 7.4

Это условие является очевидным, так как выходной сигнал звена не может возникнуть раньше входного .

Весовая функция позволяет определить реакцию звена на входной сигнал произвольной формы.

Изображение входного сигнала и.в.:

Тогда на основании теоремы свертывания выходной сигнал в любой момент времени t определится как:

,

где - вспомогательной время интегрирования, отсчитываемое от момента времени t назад, то есть справа налево.и иииио

Если входной сигнал определяется только для положительных значений аргумента, то в качестве верхнего предела интегрирования вместо t можно взять .

(1)

x

τ

0

τ₄

t₁

τ₃

t₂

τ₂

t₃

τ₁

t_ф

0

t

ω

x(t)

ω(τ)

x(t_ф-τ₄)

x(t_ф-τ₃)

x(t_ф-τ₂)

x(t_ф-τ₁)

Рис.7.5 Определение выходного сигнала по входному сигналу произв. Формы и весовой функции

Исходя из рисунка 7.5 и выражения (1), значение входного сигнала в фиксированный момент времени зависит от предыдущих значений входного сигнала умноженных на соответствующие значения весовой функции. Следовательно, функция является для отдельных значений входного сигнала весовым множителем, т.е. множителем, определяющим степень влияния значения входного сигнала на величину выходного сигнала в момент времени t.

Поэтому функция называется функцией веса или весовой функцией.

Обе временные характеристики и являются динамическими характеристиками и также полностью описывают свойства звена как ДУ и ПФ.