4.3.2.Графический конвейер

Первые графические процессоры были предназначены для решения только одной задачи – построения изображений (включая проекции 3-мер­ных сцен) на дисплее. При этом использовался графический конвейер (см., например, [14]), показанный на рис. 4.6.

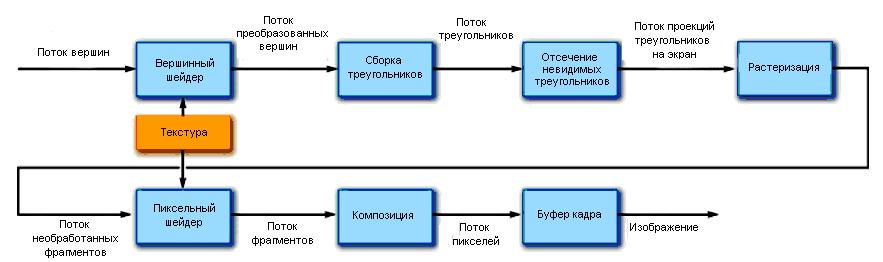
Рис. 4.6. Графический конвейер

Входными данными для графического конвейера являются:

 координаты вершин, задающих положение изображаемых плоскос­тей в трёхмерном пространстве;

 текстуры, представляющие собой массивы с данными о цветах этих плоскостей.

Графический конвейер осуществлял проектирование вершин треугольников, образующих поверхности в 3-мерном пространстве «за» плоскостью экрана на эту плоскость экрана, а затем – нанесение на эти треугольники необходимых цветов (текстур). Для проектирования вершин использовались линейные преобразования координат (т.е., матричные операции), а для нанесения необходимого рисунка на поверхности треугольников – различные алгоритмы наложения цветов видимых объектов и учёта освещённости.

Стандартные процедуры проектирования вершин и расчёта цветов на видеокартах автоматизированы, однако этих стандартных процедур недостаточно для реализации всех эффектов, используемых для отображения 3D-сцен. Поэтому появилась возможность произвольного программирования этапов проектирования вершин и закрашивания треугольников для получения уникальных эффектов. Процедуру, осуществляющую «пользовательские» действия на этапе проектирования вершин называют вершинным шейдером, а на этапе закрашивания треугольников (т.е. – определения цветов пикселей на экране) – пиксельным шейдером. Поскольку в эти процедуры может быть записан произвольный код (реализуемый операциями, доступными графическому процессору), они могут быть использованы не только для вывода графики, но и для других расчётов, на чём и основана возможность использования видеокарт при физико-математическом моделировании.

4.3.3.История программируемости графических процессоров

Первые графические процессоры для ПК, появившиеся в 1995 году (GPU 3DFX Voodoo), не были программируемыми, они только линейно отображали треугольники на плоскость экрана. Затем GPU стали исполь­зовать для трассировки лучей – расчета освещенности поверхностей, а также других графических эффектов, для чего и потребовалась программируемость графического конвейера. Следующая хронология (см., например, [15]) пока­зывает, как постепенно увеличивались возможности программирования раз­лич­ных типов GPU для обработки трёхмерной графики и выполнения поль­зовательских алгоритмов.

 1995 год, первые графические процессоры (S3 ViRGE, ATI Rage - ATI Radeon 7500, Matrox Mystique, 3dfx Voodoo)

Были разработаны как специализированные процессоры для ускорения операций с двух- и трёхмерной графикой, в частности – для отображения на плоскости экрана трёхмерных сцен. В качестве исходных данных принимали координаты вершин треугольников, образующих трёхмерные поверхности, цвета вершин, а также положение экрана и источников света относительно этой 3D-сцены. Такие GPU автоматически выполняли

 проектирование треугольников на плоскость экрана,

 интерполяционную закраску изображений этих треугольников по цветам вершин,

 нанесение заданных текстур (узоров) на изображение,

 расчёт освещённости без учёта теней, а также

 отсечение невидимых поверхностей при помощи специального буфера глубины (Z-буфера).

Программировать эти графические процессоры самостоятельно было невозможно.

 1999 год. Графические процессоры (серия NVIDIA GeForce) начинают работать с 32-битными вещественными числами, т.е. – с вещественными числами одинарной точности (7-8 значащих цифр)

Одинарной точности в принципе достаточно для моделирования физических систем, при условии применения агоритмов, корректирующих вычислительную погрешность, и проведения расчётов, критичных к точности, на центральном процессоре. Предыдущие GPU работали с числами «половинной» точности (16-битными числами), чего было заведомо недостаточно для точного физического моделирования.

С другой стороны, 32-битная точность была реализована ещё не полностью, промежуточные вычисления проводились с «половинной» точностью. Кроме того, первые процессоры серии GeForce по-прежнему не были программируемыми.

 2001 год. Появление возможности пользовательского програм­миро­вания процедур проектирования треугольников на плоскость экрана, расчёта освещённости и цвета отображаемых поверхностей.

От английского слова shade, имеющего значения «отбрасывать тень» и «заштриховывать», программы для графических процессоров стали называть шейдерами. Шейдеры позволяли выполнять над данными такие операции, как сложение, умножение, деление, вычисление квадратного корня, тригонометрических функций, экспоненты.

Шейдеры позволили реализовывать на GPU алгоритмы, не обязательно предназначенные для обработки графики. Таким образом, появилась возможность программирования GPU для решения различных задач, в том числе и задач физического моделирования.

Совокупность возможностей программирования, обеспечиваемых графическим процессором, принято называть шейдерной моделью. Первым программируемым GPU соответствовала шейдерная модель 1.0, имевшая серьёзные ограничения: длина шейдера не превосходила 20 команд, вычисления производились с «фиксированной» точкой (без использования порядковых множителей), ветвления алгоритмов не поддерживались.

Писать шейдеры сначала нужно было на специальном ассемблере. Позже появились высокоуровневые шейдерные языки программирования, такие как HLSL.

Пример GPU с шейдерной моделью 1.0 – серии NVidia GeForce 3-5.

· 2003 год. Полная реализация 32-битной точности при всех операциях с данными. Поддержка новыми графическими процессорами (NVIDIA GeForce FX, ATI Radeon 8500 - X800) шейдерной модели 2.0.

Шейдерная модель 2.0 (SM2) позволяла составлять программы длиной до 512 инструкций, а также использовать 22 регистра (быстрые ячейки памяти, расположенные прямо на процессоре) с произвольным доступом к памяти (то есть, с возможностью чтения и записи данных в произвольном порядке)

· 2004 год. Появление шейдерной модели 3.0 (GPU NVIDIA GeForce серий 6 и 7, ATI Radeon X1500 – X1950),

В шейдерной модели 3.0 (SM3) появились возможность программирования циклов (до 255 итераций) и динамическое ветвление (применение условных операторов). Максимальная длина программы выросла до 1024 инструкций, количество регистров увеличилось до 32.

· 2007 год. Графические процессоры с шейдерной моделью 4.0 (NVIDIA GeForce 8, AMD HD3). Фактический отказ от обязательной структуры программы в виде графического конвейера в пользу произвольной структуры программ.

Во всех предыдущих графических процессорах раздельно использовались вершинные и пиксельные конвейеры, решавшие различные задачи (при обработке графики – проектирование вершин и закрашивание треугольников, соответственно). Эти конвейеры нельзя было автоматически объединить для параллельной обработки одного и того же потока данных. Конвейеры GPU шейдерной модели 4.0 являются универсальными, они все могут быть объединены для обработки одного потока данных.

В шейдерной модели 4.0 впервые реализована поддержка 32-битных целых чисел, доступны 4096 регистров, возможны 65536 инструкций, расширены возможности произвольного взаимодействия графического процессора с памятью.

 2008 год. В рамках шейдерной модели 4.0 появляется поддержка вещественных чисел двойной точности (64-битные числа, 15-16 значащих цифр). Примеры GPU - серии AMD HD4, NVIDIA GeForce 200.