2.1.Среднее и действующее значение периодической функции (тока и напряжения)

F_ср= , 13(2.10)

где f(t) – периодическая функция, T – период функции.

Ввиду симметричности синусоиды получаем, что среднее значение за период равно нулю, поэтому вводят понятие среднего значения за половину периода.

T/2

0

F_ср= = F_m;

F_ср = = F_m. 14 15(2.11)

Значительно большее значение имеет понятие действующего значения. Для его осмысления оценим тепловое действие перемен­ного и постоянного тока.

Переменный ток

W = ;

Постоянный ток

W = I²RT;

Приравняв правые части и произведя простые операции, получим

I = I_Д = , 16(2.12)

где

= = .

Подставим полученный результат под корень и получим

I = , 17(2.13)

где ( 2 .13) – среднеквадратичное, эффективное или действующее значение синусоидального тока.

Аналогично, .

Рис.2.10. Графическое изображение действующего значения

2.2.Элементы r,l,c в цепях синусоидального тока

2.2.1.Сопротивление (r)

Пусть по сопротивлению протекает синусоидальный ток с начальной фазой, равной нулю

i = I_msint. 18(2.14)

Рис.2.11. Условно-положительные направления тока и напряжения на сопротивлении

Определим падение напряжения, действую­щее на зажимах сопротивления на основании закона Ома,

u = iR = I_mRsint = U_msint. 19(2.15)

Полученный результат показывает, что напряжение изменяется в фазе с током.

Определим функцию мгновенной мощности, потребляемую R,

;

p = UI(1 – cos2t), 20(2.16)

где U, I – действующие значения.

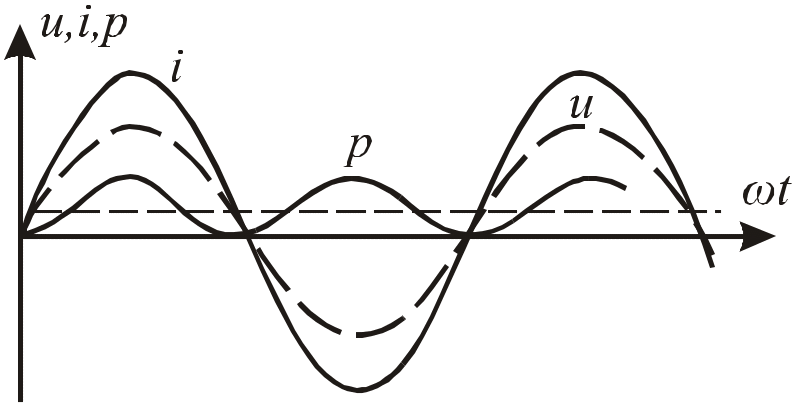
Рис.2.12. Графики мгновенных значений напряжения, тока и мощности на сопротивлении

Из графика мгновенной мощности следует, что она неотрицательна и меняется с удвоенной частотой.

Для оценки потребляемой приемником мощности вводят понятие средней мощности за период:

, [Вт]. 21(2.17)

2.2.2.Индуктивность (l)

Пусть через индуктивность протекает синусоидальный ток

i = I_msint;

Рис.2.13. Условно-положительные направления тока, напряжения и ЭДС самоиндукции

Определим падение напряжения на индуктивности u_L. На основании закона электромагнитной индукции

_L = – L = – LI_mcost = LI_msin(t–/2) = X_LI_msin(t–/2),

где – индуктивное (реактивное) сопротивление.

u_L = e_L = U_msin(t + /2). 22(2.18)

Напряжение на индуктивности опережает ток на 90⁰.

Мгновенная мощность на индуктивности

p = ui = (U_mI_msin2t)/2=UIsin2t. 23(2.19)

Среднее значение мощности за период

. 24(2.20)

Для оценки запасенной в индуктивности энергии магнитного поля вводят понятие реактивной (индуктивной) мощности

,[вар] 25(2.21)

Рис.2.14. Графики мгновенных значений напряжения, тока и мощности на индуктивности

Из графика мгновенной мощности следует, что положительная полуволна мощности соответствует потреблению энергии из сети, а отрицательная – ее возврату в сеть.

Энергия, потребляемая индуктивностью, работы не совершает.