3.Методы расчета сложных цепей

3.1.Применение законов Кирхгофа для расчета разветвленных электрических цепей

Продемонстрируем этот метод на примере схемы (Рис. 3 .42). В этой схеме 6 ветвей, то есть 6 токов, поэтому необходимо составить для их определения 6 уравнений.

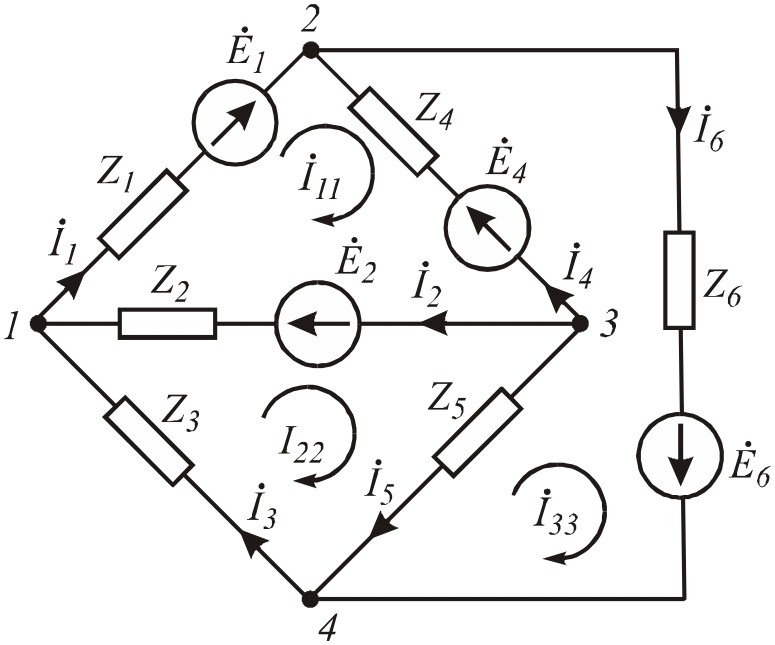
Рис.3.42. Разветвленная цепь с несколькими источниками ЭДС

Для составления уравнений зададимся произвольно положительными направлениями токов.

Уравнения по первому закону Кирхгофа:

1^ый узел: ; 74(3.71)

2^ой узел: ; 75(3.72)

4^ый узел: . 76(3.73)

Если просуммировать уравнения ( 3 .71)  ( 3 .73), то получим

,

то есть уравнение для третьего узла является избыточным, следовательно, по первому закону Кирхгофа составляем Y – 1 уравнений, где Y – число узлов схемы.

Остальные K = В  (Y  1) уравнения составляем по второму закону Кирхгофа, где K – число независимых контуров, В – число ветвей. Направления обхода контуров произвольны:

; 77(3.74)

; 78(3.75)

. 79(3.76)

Для уменьшения объема работ по расчету схемы применяют искусственные методы расчета.

3.2.Метод контурных токов

Этот метод применим для расчета любых цепей. Он базируется на уравнениях, составленных по второму закону Кирхгофа. В схеме выделяются независимые контуры, и в каждом контуре протекает свой так называемый контурный ток.

Произвольно выбираются направления контурных токов в независимых контурах (Рис. 3 .42).

80(3.77)

Используя матричный метод расчета, можем записать

. 81(3.78)

Собственное сопротивление контура – сумма соп­ротивлений, входящих в состав контура (для первого контура Z₁ +Z₂ +Z₃).

Смежные сопротивления – сопротивления на границах контуров (Z₂ и Z₄ – для первого контура).

– сумма всех ЭДС контура:

– для первого уравнения (сокращенная запись).

В ветвях, которые не граничат с другими контурами, реальные токи будут такими:

; ; .

Токи ветвей, находящихся на границах контуров:

; ; .

3.3.Метод узловых потенциалов

Метод базируется на первом законе Кирхгофа. Неизвестными для метода являются узловые потенциалы. Потенциал одного из узлов принимают равным нулю. Такое предположение допустимо, так как ток каждой ветви зависит не от абсолютных значений потенциалов узлов, а от разности потенциалов, приложенной к ветви.

Пусть потенциал узла «4» равен нулю (Рис. 3 .42). Произвольно выберем направления токов в ветвях и составим уравнения для остальных узлов на основании первого закона Кирхгофа:

«1 узел»: ;

«2 узел»: ;

«3 узел»: .

Токи в ветвях на основании закона Ома выражаются

,

где  напряжение на зажимах ветви; знаки перед и выбираются в зависимости от того, совпадает или не совпадает направление тока с положительными направлениями и . Тогда токи ветвей:

;

;

;

;

;

.

Найденные уравнения подставляются в исходную систему уравнений, составленную по первому закону Кирхгофа. Делаются несложные алгебраические преобразования, после чего получаем новую систему уравнений относительно неизвестных потенциалов :

82(3.79)

Разберем структуру любого уравнения, например, первого. Потенциал первого узла умножается на сумму проводимостей всех ветвей, образующих данный узел: Y₁+ Y₂+ Y₃. Со знаком “” записываются слагаемые вида , где Y_1k – проводимость k-ой ветви, входящей в узел 1, – потенциал соседнего (смежного) узла.

В правой части уравнения слагаемые вида записываются со знаком “+” в том случае, если источник ЭДС направлен к рассматриваемому узлу, в противном случае – со знаком “–”.

Найденные потенциалы могут иметь различные знаки. С этими знаками значения потенциалов подставляются в уравнения для нахождения токов.