7. Производная функции. Геометрический и физический её смысл.

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.

Пусть в некоторой окрестности точки определена функция Производной функции называется такое число , что функцию в окрестности U(x₀) можно представить в виде f(x₀ + h) = f(x₀) + Ah + o(h) если существует.

Определение производной функции через предел

Пусть в некоторой окрестности точки определена функция Производной функции f в точке x₀ называется предел, если он существует,

Общепринятые обозначения производной функции y = f(x) в точке x₀

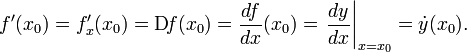
Дифференцируемость

Производная функции f в точке x₀, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x₀ тогда и только тогда, когда её производная в этой точке существует и конечна:

Для дифференцируемой в x₀ функции f в окрестности U(x₀) справедливо представление

при

1) Физический смысл производной.

Если функция y = f(x) и ее аргумент x являются физическими величинами, то производная – скорость изменения переменной y относительно переменной x в точке . Например, если S = S(t) – расстояние, проходимое точкой за время t, то ее производная – скорость в момент времени . Если q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени t, то – скорость изменения количества электричества в момент времени , т.е. сила тока в момент времени .

2) Геометрический смысл производной.

Пусть – некоторая кривая, – точка на кривой .

Любая прямая, пересекающая не менее чем в двух точках называется секущей.

Касательной к кривой в точке называется предельное положение секущей , если точка стремится к , двигаясь по кривой.

Из определения очевидно, что если касательная к кривой в точке существует, то она единственная

Рассмотрим кривую y = f(x) (т.е. график функции y = f(x)). Пусть в точке он имеет невертикальную касательную . Ее уравнение: (уравнение прямой, проходящей через точку и имеющую угловой коэффициент k).

По определению углового коэффициента , где – угол наклона прямой к оси .

Пусть – угол наклона секущей к оси , где . Так как – касательная, то при

⇒ ⇒ .

Следовательно,

.

Таким образом, получили, что – угловой коэффициент касательной к графику функции y = f(x) в точке (геометрический смысл производной функции в точке). Поэтому уравнение касательной к кривой y = f(x) в точке можно записать в виде

Замечание. Прямая, проходящая через точку перпендикулярно касательной, проведенной к кривой в точке , называется нормалью к кривой в точке . Так как угловые коэффициенты перпендикулярных прямых связаны соотношением , то уравнение нормали к кривой y = f(x) в точке будет иметь вид

, если .

Если же , то касательная к кривой y = f(x) в точке будет иметь вид , а нормаль