4. Построение эпюр при плоском изгибе.

В случае плоского поперечного изгиба в поперечных сечениях возникает два внутренних силовых фактора - поперечная сила и изгибающий момент .

Поперечная сила в сечении равна сумме проекций внешних нагрузок, действующих на отсеченную часть балки, на вертикальную ось. Если внешняя нагрузка стремится повернуть балку относительно рассматриваемого сечения по часовой стрелке, то она дает положительное слагаемое в выражении для (рис. 23).

И згибающий момент в сечении равен сумме моментов внешних нагрузок, действующих на отсеченную часть балки, относительно рассматриваемого сечения. Если внешняя нагрузка создает относительно рассматриваемого сечения момент, вызывающий сжатие верхних волокон, то она дает положительное слагаемое в выражении для (рис. 23).

Пример 1. Построить эпюры и в балке (рис. 24).

Рис. 24.

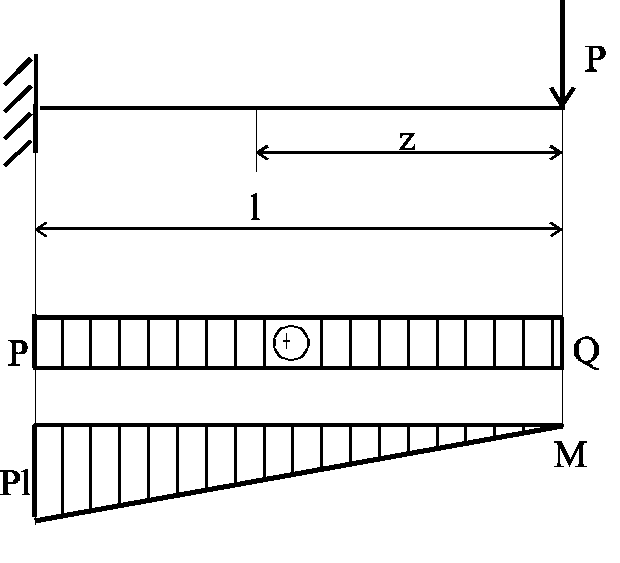
Балка имеет один участок. Записываем выражения для и в произвольном сечении с абсциссой : , . Поперечная сила постоянна в любом сечении, таким образом, эпюра имеет вид прямоугольника. Функция линейна, для построения ее графика достаточно получить две точки - в начале и конце участка: при ; при .

Пример 2. Построить эпюры и в балке (рис. 25).

Рис. 25.

Балка имеет один участок. Записываем выражения для и в произвольном сечении с абсциссой : , . Следовательно, поперечная сила изменяется по линейному закону, а изгибающий момент - по параболическому. Для построения эпюры вычисляем ординаты в двух точках: при ; при и проводим прямую.

Учитывая, что эпюра криволинейна, для ее построения вычисляем ординаты в трех сечениях:

при ; при ; при и проводим кривую через полученные три точки.

Пример 3. Построить эпюры и в балке (рис. 26).

Определяем опорные реакции. Для этого записываем уравнения статики:

.

; ,

.

; , .

Выполняем проверку

, (верно).

В балке, загруженной симметричной нагрузкой, каждая опорная реакция равна половине равнодействующей приложенной нагрузки.

.

Записываем выражения для и в произвольном сечении с абсциссой :

; .

Очевидно, что эпюра прямолинейна, а эпюра - парабола. Вычисляем:

; .

; .

Для вычисления экстремума на эпюре , приравниваем к нулю производную от изгибающего момента по абсциссе сечения:

, отсюда .

Следовательно, в сечении имеем максимальное значение момента .

В балке, загруженной симметричной нагрузкой, эпюра симметрична, эпюра - кососимметрична.

Пример 4. Построить эпюры и в балке (рис. 27).

Определяем опорные реакции:

,

.

, .

Выполняем проверку

,

На балке имеем два участка, т.к. точка приложения силы является границей участков.

Записываем выражения для и в произвольном сечении с абсциссой :

1 - й участок:

- const; - линейна.

Вычисляем ординаты эпюры на границах участка:

при ; при .

2 - й участок:

- const; - линейна.

Вычисляем ординаты эпюры на границах участка:

При ; при .

Следовательно, при функция терпит разрыв, и на эпюре получается скачок, равный по величине внешней силе в этом сечении:

,

а на эпюре имеет место перелом.

Пример 5. Построить эпюры и в балке (рис. 28).

Находим опорные реакции, направив их вверх:

;

, .

;

, .

Меняем направление на обратное.

Выполняем проверку

;

, .

На балке имеем два участка, т.к. точка приложения сосредоточенного момента является границей участка.

Записываем выражения для и в произвольном сечении с абсциссой :

1 - й участок:

- const; - линейна.

Вычисляем ординаты эпюры на границах участка:

при ; при .

2 - й участок:

- const; - линейна.

Вычисляем ординаты эпюры на границах участка:

при ; при .

Следовательно, при функция терпит разрыв, и на эпюре получается скачок, равный по величине сосредоточенному моменту в этом сечении:

,

а на эпюре изменений нет.

Пример 6. Построить эпюры и в балке (рис. 29).

Находим опорные реакции:

, .

, .

Тогда для произвольного сечения, находящегося на расстоянии от левой опоры:

, - const.

То есть, в любом сечении , а изгибающий момент постоянен. Такой случай называется чистым изгибом.