7. Уравнение трех моментов.

Расчет статически неопределимых балок проводится всегда при одинаковых основных системах, поэтому можно получить общие формулы для вычисления коэффициентов канонических уравнений и при расчете не перемножать эпюры. Рассмотрим два соседних пролета балки и и получим зависимость между неизвестными моментами , , (рис. 127).

Выписываем -ую строку системы канонических уравнений

Рассмотрим, какие слагаемые равны нулю. Строим единичные эпюры, каждая только на двух соседних пролетах. Эпюpа имеет общие участки только с и следовательно,

при

Эпюра в общем случае распространяется на всю длину балки в n-ой строке канонических уравнений остается только три слагаемых, содержащих и свободный член.

Вычислим коэффициенты

Для вычисления свободного члена вычертим эпюры и (рис. 128). Обозначим , – площади эпюры (грузовой эпюры) на соответствующих пролетах; , – центры тяжести этих площадей; , , , – расстояния от и до левой и правой опор. На эпюре из подобия вычислим ординаты под центрами тяжести , .

Подставим все данные коэффициенты в уравнение (), заменив

При расчете статически неопределимой балки составляют столько уравнений трех моментов, сколько лишних неизвестных, давая значения =1, 2, 3….

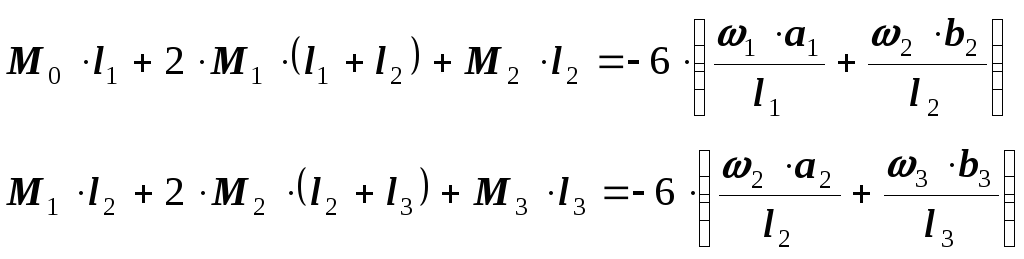
Порядок расчета по уравнению трех моментов.

1. Вычерчиваем расчетную схему (рис. 129).

2. Нумеруем слева направо: опоры, начиная с нуля, пролеты – с единицы.

3. Определяем степень статической неопределимости. Лишних неизвестных столько, сколько промежуточных опор 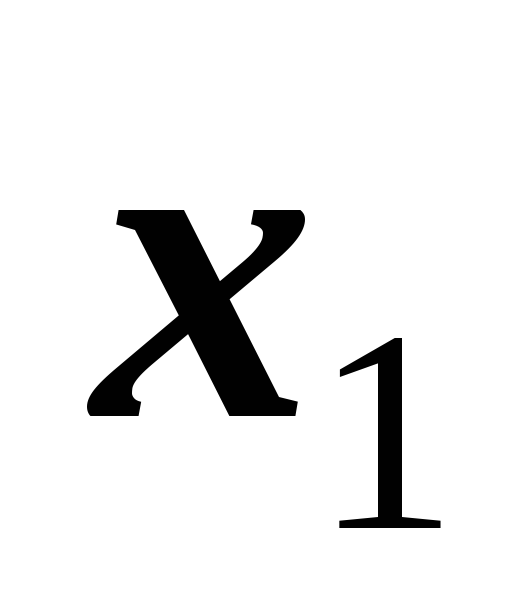, . Моменты на крайних опорах всегда известны .

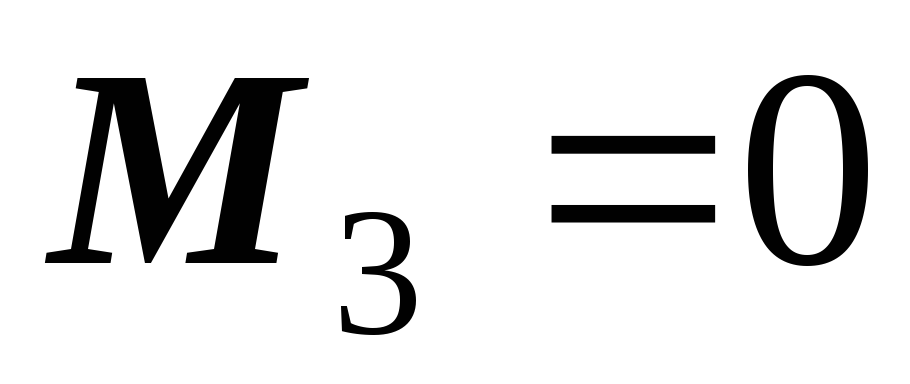4. Строим эпюры грузовых моментов (для каждого пролета как для отдельной балки). Опорные моменты не учитываем.

5. Составим нужное число уравнений. (В данном примере 2). В уравнениях должно быть все известно, кроме 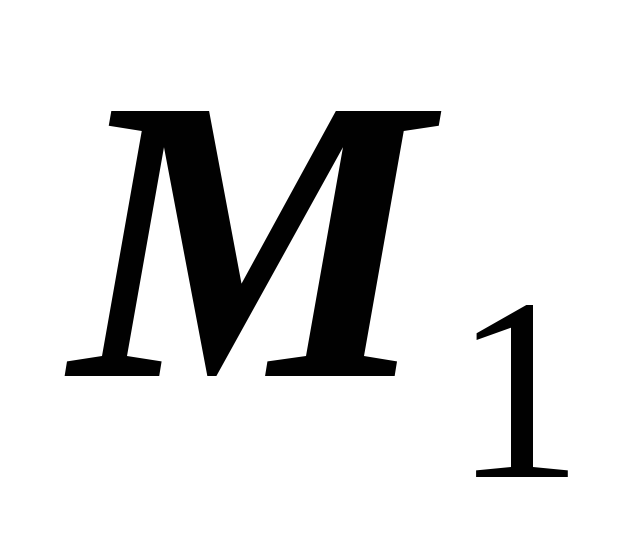и .

6. Решив систему уравнений, найдем 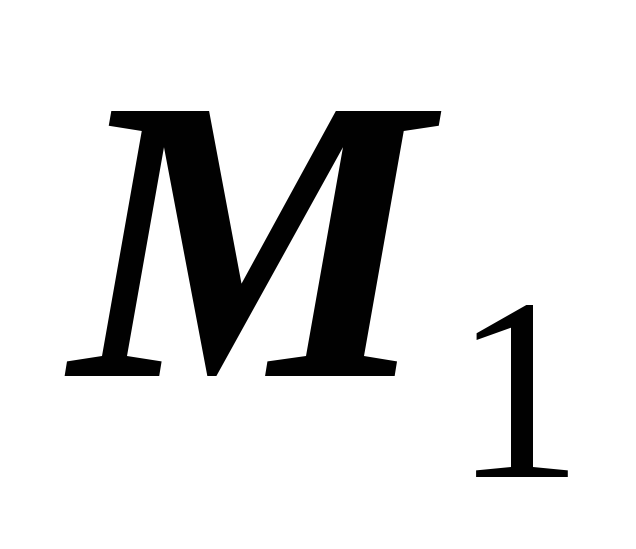,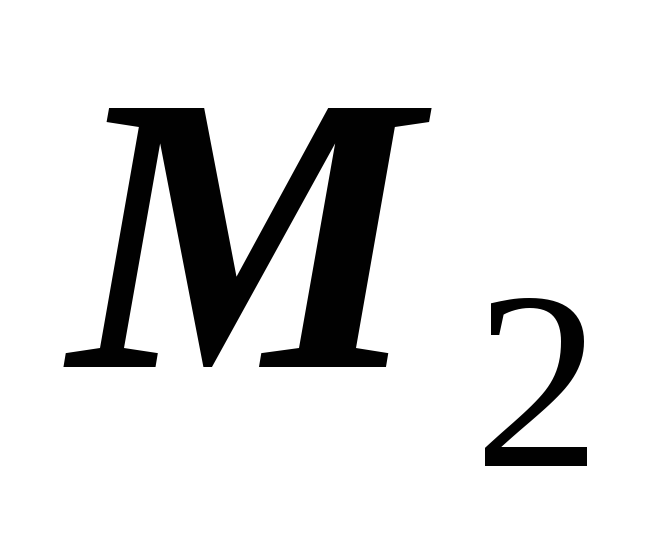. Балка становится статически определимой.

Применение уравнения трех моментов к балкам с жесткой заделкой и консолями.

1. Жесткая заделка заменяется дополнительным пролетом, длина которого в формулах принимается равной нулю (рис. 130).

2. Консоль отбрасывается и заменяется моментом на крайней опоре. Эпюра этого момента не строиться. Его численное значение подставляют в уравнение трех моментов с соответствующим знаком.

; ; ; ;.

; ; .

8. Построение эпюры и определение опорных реакций для статически неопределимой балки.

Реакции можно определять после того, как найдены опорные моменты. Определение реакций и построение эпюры можно проводить двумя способами.

1. Заменить балку несколькими статически определимыми, разрезав ее по промежуточным шарнирам (рис. 131). В местах разреза следует приложить опорные моменты с учетом знаков.

На рисунке направления моментов соответствуют знаку ; если , надо направить их в другую сторону или в уравнения равновесия подставлять со знаком минус.

Для каждой балки отдельно находим реакции. Реакция на промежуточной опоре равна сумме реакций, полученных от соседних двух пролетов.

Зная можно строить эпюру обычным способом.

2. По известной окончательной эпюре моментов можно построить

эпюру , используя дифференциальную зависимость и по эпюре определить реакции.

Для участка балки, где эпюра – прямая линия:

(1)

Для участка балки, где – парабола, в выражения для надо добавить слагаемые учитывающие распределенную нагрузку .

(2)

Если на участке балки с нагрузкой есть сила или момент, то полученную формулу применяют по участкам между ними

Например:

Участок .

По формуле (2)

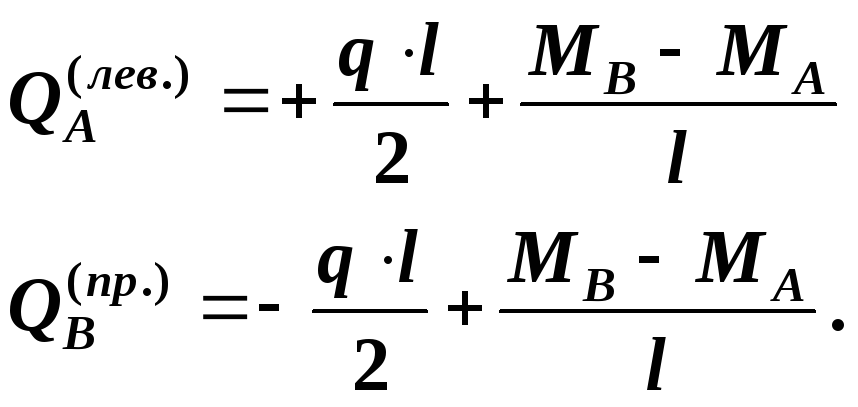
Участок ;

По формуле (1)

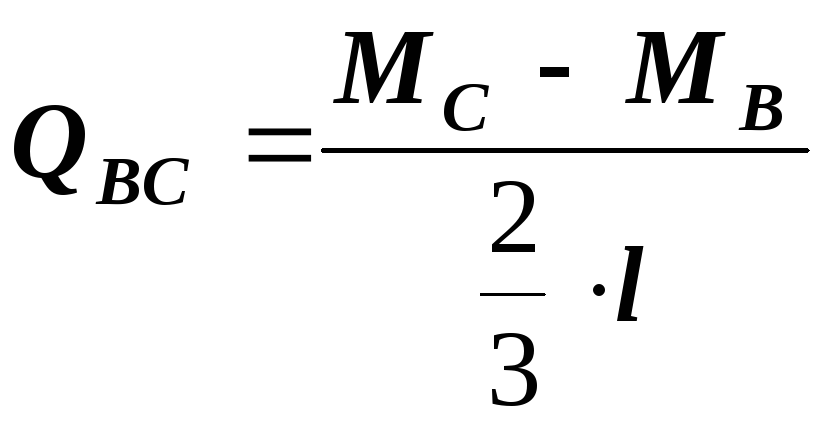
Участок ;

По формуле (1)

; ;
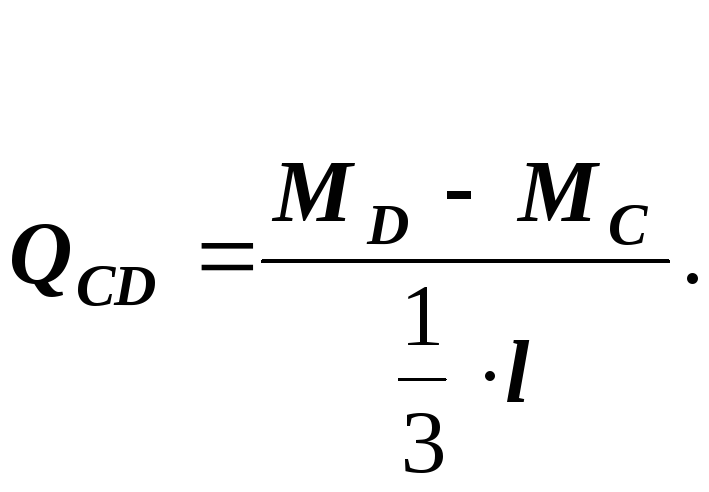