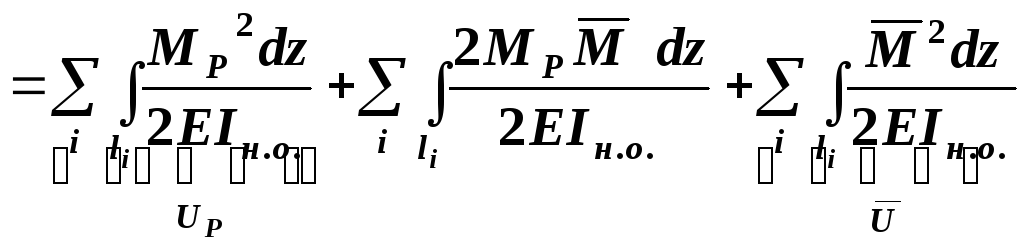- •Введение
- •1. Внешние и внутренние силы. Деформируемое тело.
- •2. Реальный объект и расчетная схема.
- •3. Основные допущения и гипотезы, принятые в
- •4. Метод сечений.
- •5. Понятие о напряжении. Предельное и допускаемое
- •6. Понятие о деформированном состоянии материала.
- •Геометрические характеристики плоских сечений
- •1. Статические моменты площади. Центр тяжести.
- •2. Моменты инерции плоских фигур.
- •3. Моменты инерции сложных сечений.
- •4. Моменты инерции относительно параллельных осей.
- •5. Зависимости моментов инерции при повороте
- •6. Определение направления главных осей.
- •Построение эпюр внутренних силовых факторов
- •1. Построение эпюр продольных сил при растяжении (сжатии).
- •2. Построение эпюр крутящих моментов.
- •3. Понятие о плоском поперечном изгибе. Балки и их опоры.
- •4. Построение эпюр при плоском изгибе.
- •5. Дифференциальные зависимости при изгибе.
- •Растяжение и сжатие
- •1. Напряжения в поперечных сечениях
- •2. Напряжения на наклонных площадках
- •3. Деформации при растяжении и сжатии. Закон Гука.
- •4. Условие прочности при растяжении. Типы задач.
- •5. Статически неопределимые конструкции.
- •6. Монтажные и температурные напряжения.
- •Опытное изучение механических свойств материалов
- •1. Опытное изучение свойств материалов при одноосном
- •2. Диаграмма растяжения стали марки сталь 3.
- •3. Разгрузка и повторное нагружение. Наклеп.
- •4. Диаграммы растяжения других конструкционных материалов
- •5. Испытание конструкционных материалов на сжатие.
- •Кручение
- •1. Чистый сдвиг. Закон Гука при чистом сдвиге.
- •2. Напряжения и деформации при кручении бруса
- •3. Расчет валов на прочность и жесткость при кручении.
- •4. Кручение стержней прямоугольного сечения.
- •Плоский изгиб
- •1. Нормальные напряжения при плоском изгибе.
- •2. Напряженное состояние прямого бруса
- •3. Расчет балок на прочность
- •4. Рациональные формы поперечных сечений балки
- •Перемещения при изгибе.
- •Основные понятия.
- •2. Дифференциальное уравнение упругой линии.
- •Определение прогибов непосредственным интегрированием
- •Метод уравнивания произвольных постоянных
- •5. Понятие о начальных параметрах.
- •Универсальное уравнение прогибов. (Уравнение метода
- •7. Примеры определения прогибов, расчет на жесткость.
- •8. Проверка балок на жесткость.
- •Теория напряженного и деформированного состояния в точке
- •1. Напряженное состояние в точке. Тензор напряжений.
- •2. Определение напряжений на наклонных площадках
- •3. Главные напряжения. Главные площадки.
- •4. Инварианты тензора напряжений.
- •5.Октаэдрические напряжения.
- •6. Понятие о шаровом тензоре напряжений и
- •7. Относительная объемная деформация.
- •8. Обобщенный закон Гука.
- •9. Потенциальная энергия деформаций.
- •Потенциальная энергия деформации и общие
- •1. Свойства упругих тел
- •2. Работа внешних сил.
- •3. Потенциальная энергия деформации упругой системы.
- •4. Интеграл Мора для вычисления перемещений
- •Приравниваем
- •5. Частные случаи записи интеграла Мора
- •6. Порядок определения перемещений по интегралу Мора
- •7. Правило Верещагина для вычисления интеграла Мора ("перемножение" эпюр)
- •8. Практические приемы перемножения
- •9. Теорема о взаимности работ и перемещений
- •Статически неопределимые системы
- •1. Понятие о статически неопределимых системах
- •2. Метод сил. Основная и эквивалентные системы
- •3. Канонические уравнения метода сил
- •4. Порядок расчета рамы по методу сил
- •5. Использование симметрии при расчете рам
- •6. Статически неопределимые балки.
- •7. Уравнение трех моментов.
- •Вычислим коэффициенты
- •8. Построение эпюры и определение опорных реакций для статически неопределимой балки.
- •Гипотезы прочности
- •В частном случае плоского напряженного состояния при , , условие прочности записывается в виде
- •Сложное сопртивление
- •2. Изгиб с растяжением (сжатием)
- •3. Косой изгиб. Пространственный изгиб.
- •4. Внецентренное сжатие (растяжение)
- •5. Изгиб с кручением круглых брусьев.
- •6. Изгиб с кручением прямоугольных брусьев.
3. Потенциальная энергия деформации упругой системы.
Ее выражение через внутренние силовые факторы.
З адана
произвольная упругая система, загруженная
произвольными нагрузками (рис. 101).
Требуется вычислить потенциальную
энергию деформации.
адана
произвольная упругая система, загруженная
произвольными нагрузками (рис. 101).
Требуется вычислить потенциальную
энергию деформации.
Вырежем
из системы элемент длиной
![]() .
В общем
случае нагружения в сечениях будет
действовать по шесть силовых факторов.
.
В общем
случае нагружения в сечениях будет
действовать по шесть силовых факторов.
![]() -
продольная сила, соответствующая
растяжению-сжатию
-
продольная сила, соответствующая
растяжению-сжатию
 -
поперечные силы, соответствующие изгибу
-
поперечные силы, соответствующие изгибу
![]() -
крутящий момент
-
крутящий момент
![]() -
изгибающие моменты
-
изгибающие моменты
Потенциальную энергию, накопленную в элементе при деформации, можно вычислить как работу силовых факторов, действующих в сечениях. Работа их будет действительной, т. к. по мере нагружения системы внешними нагрузками силовые факторы в сечении и перемещения постепенно увеличивается. Работы внутренних силовых факторов независимы, так как каждый работает только на своем перемещении. Можно вычислять работу от каждого силового фактора отдельно.
1 .
От продольной силы (рис. 102):
.
От продольной силы (рис. 102):
![]()
где
-
![]() закон Гука
закон Гука
2. От изгибающего момента (рис. 103):

![]()
![]()
![]()
В
общем случае нагружения будет два
изгибающих момента во взаимно
перпендикулярных плоскостях
![]() и
и
![]() .
Соответственно
.
Соответственно
![]() будет состоять из двух слагаемых
будет состоять из двух слагаемых
![]()

3. От крутящего момента (рис. 104):
![]()
![]()
![]()
4.
По аналогии можно записать выражение
![]() от поперечных сил, хотя в расчетах они
обычно не учитываются
от поперечных сил, хотя в расчетах они
обычно не учитываются
![]()
где
![]() и
и
![]() - коэффициенты,
учитывающие форму сечения.
- коэффициенты,
учитывающие форму сечения.
Чтобы вычислить потенциальную энергию деформации всей системы нужно полученные выражения элементарной энергии от каждого силового фактора проинтегрировать по участкам и затем эти интегралы сложить

В практических расчетах обычно все интегралы не приходится вычислять, так как величины энергии, соответствующие разным силовым факторам могут отличаться на один- два порядка.
При
плоском изгибе в балках и рамах учитывают
только один изгибающий момент
![]() или
или
![]() ;
;
при
расчете шарнирных стержневых систем
- только продольную силу
![]() ;
;
в
пространственных системах учитывают
изгибающие моменты в двух главных
плоскостях и крутящий момент
![]() ,
,
![]() и
и
![]() .
.
4. Интеграл Мора для вычисления перемещений
произвольно нагруженных брусьев
Вывод
формулы проводится для случая плоского
изгиба, соответственно учитывается
только изгибающий момент
![]() .
В общем случае нагружения рассуждения
аналогичны.
.
В общем случае нагружения рассуждения
аналогичны.
Постановка задачи:
Задана
произвольная упругая система, загруженная
силами
![]() .
Требуется определить перемещение
произвольной точки
.
Требуется определить перемещение
произвольной точки
![]() в заданном
направле-
в заданном
направле-
нии
![]() .
.
Для
вывода формулы кроме заданной рассмотрим
вспомогательную единичную систему,
которая представляет собой заданную
упругую систему (рис. 105), к которой
по направлению искомого перемещения
приложена единичная сила
![]() .
.
В ведем
обозначения:
ведем
обозначения:
в заданной системе -
изгибающий
момент -
![]()
работа
внешних сил -
![]()
энергия деформации -
-

в единичной системе -
изгибающий
момент -
![]()
работа
силы -
![]()
энергия деформации -
-
![]()
По первому свойству упругих систем справедливы равенства:
![]()
![]()
Вывод формулы:
Загрузим
систему последовательно сначала
единичной силой
![]() ,
а затем, не
снимая ее, заданными силами
,
а затем, не
снимая ее, заданными силами
![]() .
Из равенства энергии и работы после
двух нагружений можно найти перемещение
.
Из равенства энергии и работы после
двух нагружений можно найти перемещение
![]() .
.
Работа
после первого нагружения ![]() ,
,
после
второго нагружения
![]() ,
,
суммарная
![]() ,
,
Изгибающий
момент после двух нагружений
![]()
Вычисляем
![]()

![]()